| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
 Postano: 18:40 čet, 22. 10. 2009 Naslov: Zadaci iz zadaća Postano: 18:40 čet, 22. 10. 2009 Naslov: Zadaci iz zadaća |
    |
|
|
Zanima me može li netko riješiti 5 i 7 zadatak iz prve zadaće koja stoji na web stranici kolegija??
5. Koliko ima permutacija skupa {1,2,......n} takvih da nikoja dva od 1,2,3 nisu susjedni?
7. Odredite broj najkraćih puteva u cjelobrojnoj mreži od točke (0,0) do točke (m,n)(m,n>=8) koji prolaze kroz točku (2,3) i segment [(4,4),(4,5)], a ne kroz točku (7,7).
Zanima me može li netko riješiti 5 i 7 zadatak iz prve zadaće koja stoji na web stranici kolegija??
5. Koliko ima permutacija skupa {1,2,......n} takvih da nikoja dva od 1,2,3 nisu susjedni?
7. Odredite broj najkraćih puteva u cjelobrojnoj mreži od točke (0,0) do točke (m,n)(m,n>= koji prolaze kroz točku (2,3) i segment [(4,4),(4,5)], a ne kroz točku (7,7). koji prolaze kroz točku (2,3) i segment [(4,4),(4,5)], a ne kroz točku (7,7).
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 19:40 čet, 22. 10. 2009 Naslov: Postano: 19:40 čet, 22. 10. 2009 Naslov: |
    |
|
|
5.
permutiras {4,5,...,n} na (n-4+1)! nacina, i onda izmedu ubacujes 1, 2 i 3, jedinicu mozes na stavit na (n-3+1)=(n-2) nacina, 2icu na jedan manje i 3 jos jedan manje od toga dakle rjesenje je
(n-3)!(n-2)(n-3)(n-4)=(n-2)!(n-3)(n-4)
7 budem kasnije ako ga nitko ne rjesi, moram sad nest iz linearne rjesit
5.
permutiras {4,5,...,n} na (n-4+1)! nacina, i onda izmedu ubacujes 1, 2 i 3, jedinicu mozes na stavit na (n-3+1)=(n-2) nacina, 2icu na jedan manje i 3 jos jedan manje od toga dakle rjesenje je
(n-3)!(n-2)(n-3)(n-4)=(n-2)!(n-3)(n-4)
7 budem kasnije ako ga nitko ne rjesi, moram sad nest iz linearne rjesit
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 20:52 čet, 22. 10. 2009 Naslov: Postano: 20:52 čet, 22. 10. 2009 Naslov: |
    |
|
|
dakle "isti" zad imas na vjezbama
najkraci put do neke tocke se sastoji od par puta gore i par puta desno
i jos se bavis tim uvjetima
dakle moras prvo doc do (2,3), dakle 2 puta desno i 3 puta gore
to mozes na [latex]\displaystyle\left(\begin{array}{c} 5 \\ 2\end{array}\right) [/latex]nacina, moras samo odabrat kad ces ic desno, ostalo ides gore, zatim moras ic od (2,3) do (4,4) to mozes na [latex]\displaystyle\left(\begin{array}{c} 4-2+4-3 \\ 4-2\end{array}\right) [/latex] nacina i sad jos gledas kako od (4,5) doci do (m,n) bez da prodes kroz (7,7)
izracunas kako doc od (4,5) do (m,n), zatim izracunas kako doc tako da prodes kroz (7,7) i to oduzmes, dakle [b]valjda[/b] je ukupno rjesenje
[latex]\displaystyle\left(\begin{array}{c} 5 \\ 2\end{array}\right) \left(\begin{array}{c} 3 \\ 1\end{array}\right)\left[ \left(\begin{array}{c} m+n-9 \\ m-4\end{array}\right)-\left(\begin{array}{c} 5 \\ 2\end{array}\right)\left(\begin{array}{c} m+n-14 \\ m-7\end{array}\right)\right][/latex]
dakle "isti" zad imas na vjezbama
najkraci put do neke tocke se sastoji od par puta gore i par puta desno
i jos se bavis tim uvjetima
dakle moras prvo doc do (2,3), dakle 2 puta desno i 3 puta gore
to mozes na 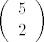 nacina, moras samo odabrat kad ces ic desno, ostalo ides gore, zatim moras ic od (2,3) do (4,4) to mozes na nacina, moras samo odabrat kad ces ic desno, ostalo ides gore, zatim moras ic od (2,3) do (4,4) to mozes na 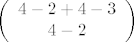 nacina i sad jos gledas kako od (4,5) doci do (m,n) bez da prodes kroz (7,7) nacina i sad jos gledas kako od (4,5) doci do (m,n) bez da prodes kroz (7,7)
izracunas kako doc od (4,5) do (m,n), zatim izracunas kako doc tako da prodes kroz (7,7) i to oduzmes, dakle valjda je ukupno rjesenje
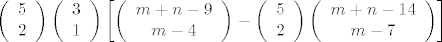
_________________
Mario Berljafa
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:20 čet, 22. 10. 2009 Naslov: Postano: 21:20 čet, 22. 10. 2009 Naslov: |
    |
|
|
[color=darkred]People, [b]nema[/b] rjesavanja zadaca! Dajte upute, pomozite,... ali nemojte pljuckati van gotova rjesenja; to ne sluzi nicemu korisnom![/color]
People, nema rjesavanja zadaca! Dajte upute, pomozite,... ali nemojte pljuckati van gotova rjesenja; to ne sluzi nicemu korisnom!
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:46 čet, 22. 10. 2009 Naslov: Postano: 22:46 čet, 22. 10. 2009 Naslov: |
    |
|
|
:oops:
[color=darkred]Ok, ispricavam se, nisam znao.[/color]
No, i dalje je korisnije hintirati nego skroz rijesiti. ;)

Ok, ispricavam se, nisam znao.
No, i dalje je korisnije hintirati nego skroz rijesiti. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
whateveryouwant
Forumaš(ica)

Pridružen/a: 02. 11. 2008. (18:27:38)
Postovi: (2F)16
|
|
| [Vrh] |
|
|







