| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
 Postano: 21:57 pet, 31. 10. 2008 Naslov: Postano: 21:57 pet, 31. 10. 2008 Naslov: |
    |
|
|
to ti ja valjda mogu pomoći...
[latex]\frac{1}{2ln^22} + \frac{1}{6ln^22} +...+\frac{1}{n(n-1)ln^22}[/latex]
[latex]\sum_{k=1}^{n(n-1)}\frac{1}{k(k-1)ln^22}[/latex]
odnosno, ako prije izlučiš dobiješ...
[latex]\frac{1}{ln^22}\sum_{k=1}^{n(n-1)}\frac{1}{k(k-1)}[/latex]
i dalje ne znam jer ne znam redove, a ni limese, a valjda sam nekako pomogao :D
[quote]Koliko se sjećam, da... 2.semestar (analiza 2) su derivacije i integrali.[/quote]
Lijepo. Nagledati ću se toga :D
to ti ja valjda mogu pomoći...
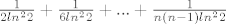
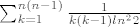
odnosno, ako prije izlučiš dobiješ...
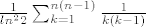
i dalje ne znam jer ne znam redove, a ni limese, a valjda sam nekako pomogao 
| Citat: | | Koliko se sjećam, da... 2.semestar (analiza 2) su derivacije i integrali. |
Lijepo. Nagledati ću se toga 
_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:52 pet, 31. 10. 2008 Naslov: Postano: 22:52 pet, 31. 10. 2008 Naslov: |
    |
|
|
[quote="tuv0k"]
[quote]Koliko se sjećam, da... 2.semestar (analiza 2) su derivacije i integrali.[/quote]
Lijepo. Nagledati ću se toga :D[/quote]
A tek na 2.god... tu ima svakakvih vrsta integrala... meni jako zanimljivo... a vidim ja da ćeš ti nama doći... odlično, odlično... :D
@vriskica A ne brini, nije ti to tak teško, samo se igraš s izrazima i probaš doć do nečeg poznatog... kad uđeš u to, bit će lakše ;)
| tuv0k (napisa): |
| Citat: | | Koliko se sjećam, da... 2.semestar (analiza 2) su derivacije i integrali. |
Lijepo. Nagledati ću se toga  |
A tek na 2.god... tu ima svakakvih vrsta integrala... meni jako zanimljivo... a vidim ja da ćeš ti nama doći... odlično, odlično... 
@vriskica A ne brini, nije ti to tak teško, samo se igraš s izrazima i probaš doć do nečeg poznatog... kad uđeš u to, bit će lakše 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 0:05 sub, 1. 11. 2008 Naslov: Postano: 0:05 sub, 1. 11. 2008 Naslov: |
    |
|
|
[quote="tuv0k"]to ti ja valjda mogu pomoći...
[latex]\frac{1}{2ln^22} + \frac{1}{6ln^22} +...+\frac{1}{n(n-1)ln^22}[/latex]
[latex]\sum_{k=1}^{n(n-1)}\frac{1}{k(k-1)ln^22}[/latex]
odnosno, ako prije izlučiš dobiješ...
[latex]\frac{1}{ln^22}\sum_{k=1}^{n(n-1)}\frac{1}{k(k-1)}[/latex]
[/quote]
Ova suma baš i ne odgovara članu [latex] a_n [/latex], za k=1, dobiješ [latex] \frac{1}{0} [/latex]
Mislim da ti treba [latex] a_n=\frac{1}{ln^22} \sum_{k=1}^{n-1} \frac{1}{k(k+1)} [/latex], ovo vrijedi za n>1, za n=1 [latex] a_n
[/latex] nije definiran.
A ova suma [latex] \frac{1}{ln^22}\sum_{k=1}^{n-1} \frac{1}{k(k+1)}= \frac{1}{ln^22}\sum_{k=1}^{n-1} (\frac{1}{k}-\frac{1}{k+1})[/latex]
U ovoj sumi se svi članovi pokrate osim prvog i zadnjeg pa ostane:
[latex] \frac{1}{ln^22} (1-\frac{1}{n}) [/latex]
I sada [latex] \frac{1}{ln^22}[lim_{n\to +\infty} (1-\frac{1}{n})]=\frac{1}{ln^22} [/latex]
| tuv0k (napisa): | to ti ja valjda mogu pomoći...
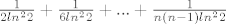
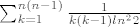
odnosno, ako prije izlučiš dobiješ...
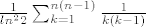
|
Ova suma baš i ne odgovara članu 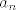 , za k=1, dobiješ , za k=1, dobiješ 
Mislim da ti treba 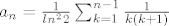 , ovo vrijedi za n>1, za n=1 , ovo vrijedi za n>1, za n=1 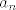 nije definiran. nije definiran.
A ova suma 
U ovoj sumi se svi članovi pokrate osim prvog i zadnjeg pa ostane:
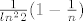
I sada 
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
|












