| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 20:35 sub, 1. 11. 2008 Naslov: 2. zadaca Postano: 20:35 sub, 1. 11. 2008 Naslov: 2. zadaca |
    |
|
|
bok, molio bih (za pocetak ;)) pomoc oko 9. b) zadatka iz [url=http://web.math.hr/nastava/komb/zadace/zadaca2.pdf]zadace[/url], koji glasi:
neka je dan skup [latex]A[/latex] od [latex]n[/latex] elemenata,
odredite koliko ima bijekcija [latex]f:A \rightarrow A[/latex] koje su same sebi inverz i nemaju fiksnih tocaka.
ovo "da nemaju fiksnih tocaka" znaci [latex](\forall a \in A)[/latex], [latex]f(a) \neq a[/latex], jel da? to znaci da je iskljucena bijekcija f(1)=1, f(2)=2,... itd.
znaci da bi jedna bijekcija koja je sama sebi inverz, i bez fiksnih tocaka, ako uzmemo A={1,2,3,4}, bila npr. f(1)=3, f(2)=4, f(3)=1, f(4)=2.
E sad, kako prebrojati sve takve bijekcije na n-clanom skupu? :neznam:
zahvaljujem
bok, molio bih (za pocetak  ) pomoc oko 9. b) zadatka iz zadace, koji glasi: ) pomoc oko 9. b) zadatka iz zadace, koji glasi:
neka je dan skup  od od  elemenata, elemenata,
odredite koliko ima bijekcija 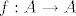 koje su same sebi inverz i nemaju fiksnih tocaka. koje su same sebi inverz i nemaju fiksnih tocaka.
ovo "da nemaju fiksnih tocaka" znaci 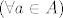 , , 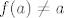 , jel da? to znaci da je iskljucena bijekcija f(1)=1, f(2)=2,... itd. , jel da? to znaci da je iskljucena bijekcija f(1)=1, f(2)=2,... itd.
znaci da bi jedna bijekcija koja je sama sebi inverz, i bez fiksnih tocaka, ako uzmemo A={1,2,3,4}, bila npr. f(1)=3, f(2)=4, f(3)=1, f(4)=2.
E sad, kako prebrojati sve takve bijekcije na n-clanom skupu? 
zahvaljujem
_________________  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:51 sub, 1. 11. 2008 Naslov: Re: 2. zadaca Postano: 20:51 sub, 1. 11. 2008 Naslov: Re: 2. zadaca |
    |
|
|
[quote="gaston"]znaci da bi jedna bijekcija koja je sama sebi inverz, i bez fiksnih tocaka, ako uzmemo A={1,2,3,4}, bila npr. f(1)=3, f(2)=4, f(3)=1, f(4)=2.[/quote]
Ovdje si na dobrom tragu. Pogledaj npr. što se dešava sa elementima 1 i 3 skupa A. f(1)=3 i f(3)=1, to jest, skup {1,3} se mora preslikti u samog sebe, ali tako da nema fiksnih točaka. Ista stvar vrijedi za bilo koji dvočlani podskup tvog skupa A.
Ako još ne vidiš što bi trebao prebrojati, probaj isti "pokus" napraviti kada je A={1,2,3,4,5} i A={1,2,3,4,5,6}. Iz toga ćeš zaključiti nešto o (ne)parnosti broja n i što trebaš prebrojati da bi dobio broj traženih bijekcija.
| gaston (napisa): | | znaci da bi jedna bijekcija koja je sama sebi inverz, i bez fiksnih tocaka, ako uzmemo A={1,2,3,4}, bila npr. f(1)=3, f(2)=4, f(3)=1, f(4)=2. |
Ovdje si na dobrom tragu. Pogledaj npr. što se dešava sa elementima 1 i 3 skupa A. f(1)=3 i f(3)=1, to jest, skup {1,3} se mora preslikti u samog sebe, ali tako da nema fiksnih točaka. Ista stvar vrijedi za bilo koji dvočlani podskup tvog skupa A.
Ako još ne vidiš što bi trebao prebrojati, probaj isti "pokus" napraviti kada je A={1,2,3,4,5} i A={1,2,3,4,5,6}. Iz toga ćeš zaključiti nešto o (ne)parnosti broja n i što trebaš prebrojati da bi dobio broj traženih bijekcija.
_________________
The Dude Abides
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 21:05 sub, 1. 11. 2008 Naslov: Re: 2. zadaca Postano: 21:05 sub, 1. 11. 2008 Naslov: Re: 2. zadaca |
    |
|
|
[quote="goranm"]
Ovdje si na dobrom tragu. Pogledaj npr. što se dešava sa elementima 1 i 3 skupa A. f(1)=3 i f(3)=1, to jest, skup {1,3} se mora preslikti u samog sebe, ali tako da nema fiksnih točaka. Ista stvar vrijedi za bilo koji dvočlani podskup tvog skupa A.
Ako još ne vidiš što bi trebao prebrojati, probaj isti "pokus" napraviti kada je A={1,2,3,4,5} i A={1,2,3,4,5,6}. Iz toga ćeš zaključiti nešto o (ne)parnosti broja n i što trebaš prebrojati da bi dobio broj traženih bijekcija.[/quote]
ahaa, kuzim. ustvari trazim broj svih mogucih particija n-clanog skupa na (disjunktne) dvoclane podskupove. ali ako je n neparan, onda ce, nakon sto svih (n-1) elemenata bude spareno, ostati jedan element koji ce se morati preslikati u samog sebe, a takve funkcije ne uzimamo u obzir. dakle, broj takvih funkcija je 0 za n neparan (jer nuzno postoji fiksna tocka)
e sad, ako je n paran, onda je sa Stirlingovim brojem druge vrste [latex]S(n,k)[/latex] dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje [latex]k=\frac{n}{2}[/latex].
ne? :)
| goranm (napisa): |
Ovdje si na dobrom tragu. Pogledaj npr. što se dešava sa elementima 1 i 3 skupa A. f(1)=3 i f(3)=1, to jest, skup {1,3} se mora preslikti u samog sebe, ali tako da nema fiksnih točaka. Ista stvar vrijedi za bilo koji dvočlani podskup tvog skupa A.
Ako još ne vidiš što bi trebao prebrojati, probaj isti "pokus" napraviti kada je A={1,2,3,4,5} i A={1,2,3,4,5,6}. Iz toga ćeš zaključiti nešto o (ne)parnosti broja n i što trebaš prebrojati da bi dobio broj traženih bijekcija. |
ahaa, kuzim. ustvari trazim broj svih mogucih particija n-clanog skupa na (disjunktne) dvoclane podskupove. ali ako je n neparan, onda ce, nakon sto svih (n-1) elemenata bude spareno, ostati jedan element koji ce se morati preslikati u samog sebe, a takve funkcije ne uzimamo u obzir. dakle, broj takvih funkcija je 0 za n neparan (jer nuzno postoji fiksna tocka)
e sad, ako je n paran, onda je sa Stirlingovim brojem druge vrste 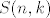 dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje  . .
ne? 
_________________  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 21:18 sub, 1. 11. 2008 Naslov: Re: 2. zadaca Postano: 21:18 sub, 1. 11. 2008 Naslov: Re: 2. zadaca |
    |
|
|
[quote="gaston"]ahaa, kuzim. ustvari trazim broj svih mogucih particija n-clanog skupa na (disjunktne) dvoclane podskupove. ali ako je n neparan, onda ce, nakon sto svih (n-1) elemenata bude spareno, ostati jedan element koji ce se morati preslikati u samog sebe, a takve funkcije ne uzimamo u obzir. dakle, broj takvih funkcija je 0 za n neparan (jer nuzno postoji fiksna tocka)
e sad, ako je n paran, onda je sa Stirlingovim brojem druge vrste [latex]S(n,k)[/latex] dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje [latex]k=\frac{n}{2}[/latex].
ne? :)[/quote]
Jeste. Osim konačnog rješenja. Npr. jedna 2-particija četveročlanog skupa A={1,2,3,4} je {{1,2,3},{4}}, a takve particije ne želimo brojati pa će S(4,2) prebrojati više nego što želimo.
Broj rastava n-članog skupa na dvočlane podskupove nije teško izbrojati. Prvo odabereš jedan dvočlani podskup, pa drugi od ostatka, pa treći....neke stvari se ponavljaju pa se mora podijeliti s nečim i tak...:)
Uostalom, mislim da eksplicitnu formulu za Stirlingov broj druge vrste još niste radili.
| gaston (napisa): | ahaa, kuzim. ustvari trazim broj svih mogucih particija n-clanog skupa na (disjunktne) dvoclane podskupove. ali ako je n neparan, onda ce, nakon sto svih (n-1) elemenata bude spareno, ostati jedan element koji ce se morati preslikati u samog sebe, a takve funkcije ne uzimamo u obzir. dakle, broj takvih funkcija je 0 za n neparan (jer nuzno postoji fiksna tocka)
e sad, ako je n paran, onda je sa Stirlingovim brojem druge vrste 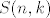 dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje dan broj particija n-clanog skupa na k dijelova, pri cemu je ovdje  . .
ne?  |
Jeste. Osim konačnog rješenja. Npr. jedna 2-particija četveročlanog skupa A={1,2,3,4} je {{1,2,3},{4}}, a takve particije ne želimo brojati pa će S(4,2) prebrojati više nego što želimo.
Broj rastava n-članog skupa na dvočlane podskupove nije teško izbrojati. Prvo odabereš jedan dvočlani podskup, pa drugi od ostatka, pa treći....neke stvari se ponavljaju pa se mora podijeliti s nečim i tak...
Uostalom, mislim da eksplicitnu formulu za Stirlingov broj druge vrste još niste radili.
_________________
The Dude Abides
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 21:38 sub, 1. 11. 2008 Naslov: Re: 2. zadaca Postano: 21:38 sub, 1. 11. 2008 Naslov: Re: 2. zadaca |
    |
|
|
[quote="goranm"]
Broj svih 2-particija n-članog skupa nije teško izbrojati.
[/quote]
jao, pa da :!:
imamo skup od n elemenata, odaberemo dva, npr. a i b, i uzmemo f(a)=b, f(b)=a. ostane nam (n-2) elementa, od kojih biramo opet bilo koja 2, dakle ukupan nacin odabira je:
[latex]\begin{pmatrix}n\\2 \end{pmatrix} \cdot \begin{pmatrix}n-2\\2 \end{pmatrix} \cdot \cdot \cdot \begin{pmatrix}2\\2 \end{pmatrix}=
\frac{n!}{2!(n-2)! } \cdot \frac{(n-2)!}{2!(n-4)! }\cdot\cdot\cdot \frac{2!}{2!0! }=$kad se sve skrati$= \frac{n!}{2^\frac{n}{2}}[/latex]
dakle, rjesenje je:
0, za n neparan
[latex]\frac{n!}{2^\frac{n}{2}}[/latex], za n paran
puno puno hvala na pomoci! :karma: reci ako je nesto krivo :)
| goranm (napisa): |
Broj svih 2-particija n-članog skupa nije teško izbrojati.
|
jao, pa da 
imamo skup od n elemenata, odaberemo dva, npr. a i b, i uzmemo f(a)=b, f(b)=a. ostane nam (n-2) elementa, od kojih biramo opet bilo koja 2, dakle ukupan nacin odabira je:
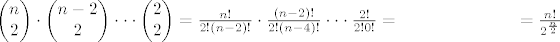
dakle, rjesenje je:
0, za n neparan
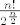 , za n paran , za n paran
puno puno hvala na pomoci!  reci ako je nesto krivo reci ako je nesto krivo 
_________________  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:07 sub, 1. 11. 2008 Naslov: Re: 2. zadaca Postano: 22:07 sub, 1. 11. 2008 Naslov: Re: 2. zadaca |
    |
|
|
[quote="rafaelm"]Ako se dobro sjećam, mi smo to zvali '[i]sparivanje[/i]', na vježbama iz diskretne.[/quote]
To je inače "broj transpozicija", a transpozicija je ciklus duljine 2. :) A kako postoji formula za broj permutacija od n elemenata cikličkog tipa (c1,c2,...,c_n), tada iz te formule za ciklički tip (0,n/2,0,...,0) odmah slijedi rješenje zadatka. :)
| rafaelm (napisa): | | Ako se dobro sjećam, mi smo to zvali 'sparivanje', na vježbama iz diskretne. |
To je inače "broj transpozicija", a transpozicija je ciklus duljine 2.  A kako postoji formula za broj permutacija od n elemenata cikličkog tipa (c1,c2,...,c_n), tada iz te formule za ciklički tip (0,n/2,0,...,0) odmah slijedi rješenje zadatka. A kako postoji formula za broj permutacija od n elemenata cikličkog tipa (c1,c2,...,c_n), tada iz te formule za ciklički tip (0,n/2,0,...,0) odmah slijedi rješenje zadatka. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 22:23 sub, 1. 11. 2008 Naslov: Postano: 22:23 sub, 1. 11. 2008 Naslov: |
    |
|
|
[quote="rafaelm"]Nije važan redosljed kojim biramo te elemente, pa bi tribalo još malo dijeliti.[/quote]
zaista! :oops:
mnozenje, tj. princip produkta koristimo kada trazimo broj uredjenih n-torki, a redoslijed dvoclanih skupova nam je u ovom zadatku nebitan. dakle, ako je n paran, onda ima [latex]\frac{n}{2}[/latex] parova elemenata iz A...
da li je onda konacno rjesenje
[latex]
(\begin{pmatrix}n\\2 \end{pmatrix} \cdot \begin{pmatrix}n-2\\2 \end{pmatrix} \cdot \cdot \cdot \begin{pmatrix}2\\2 \end{pmatrix})/(\frac{n}{2})![/latex]
:?:
| rafaelm (napisa): | | Nije važan redosljed kojim biramo te elemente, pa bi tribalo još malo dijeliti. |
zaista! 
mnozenje, tj. princip produkta koristimo kada trazimo broj uredjenih n-torki, a redoslijed dvoclanih skupova nam je u ovom zadatku nebitan. dakle, ako je n paran, onda ima 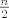 parova elemenata iz A... parova elemenata iz A...
da li je onda konacno rjesenje
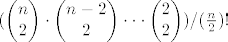

_________________  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:35 sub, 1. 11. 2008 Naslov: Postano: 22:35 sub, 1. 11. 2008 Naslov: |
    |
|
|
[quote="gaston"]da li je onda konacno rjesenje
[latex]
(\begin{pmatrix}n\\2 \end{pmatrix} \cdot \begin{pmatrix}n-2\\2 \end{pmatrix} \cdot \cdot \cdot \begin{pmatrix}2\\2 \end{pmatrix})/(\frac{n}{2})![/latex]
:?:[/quote]
Je. :)
Sad možeš vidjeti da je to isto kao broj permutacija od n elemenata cikličkog tipa [latex](0,\frac{n}{2},0,\dots,0)[/latex], to jest broj načina na koji n-člani skup možemo rastaviti u transpozicije iliti cikluse duljine 2 (ako rastavljamo samo na cikluse duljine 2, tada takvih ciklusa mora biti točno n/2, a svih ostalih očito mora biti 0).
Općenita formula za broj permutacija od n elemenata cikličkog tipa [latex](c_1,c_2,\dots,c_n)[/latex] je
[latex]\dfrac{n!}{1^{c_1}c_1!2^{c_2}c_2!\cdots n^{c_n}c_n!},[/latex]
a u našem slučaju to je
[latex]\dfrac{n!}{2^{\frac{n}{2}}(\frac{n}{2})!}[/latex]
| gaston (napisa): | da li je onda konacno rjesenje
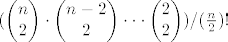
 |
Je. 
Sad možeš vidjeti da je to isto kao broj permutacija od n elemenata cikličkog tipa 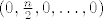 , to jest broj načina na koji n-člani skup možemo rastaviti u transpozicije iliti cikluse duljine 2 (ako rastavljamo samo na cikluse duljine 2, tada takvih ciklusa mora biti točno n/2, a svih ostalih očito mora biti 0). , to jest broj načina na koji n-člani skup možemo rastaviti u transpozicije iliti cikluse duljine 2 (ako rastavljamo samo na cikluse duljine 2, tada takvih ciklusa mora biti točno n/2, a svih ostalih očito mora biti 0).
Općenita formula za broj permutacija od n elemenata cikličkog tipa 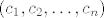 je je
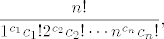
a u našem slučaju to je
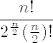
_________________
The Dude Abides
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 19:57 ned, 2. 11. 2008 Naslov: Postano: 19:57 ned, 2. 11. 2008 Naslov: |
    |
|
|
evo, ja bih upao sa jednim drugim pitanjem, vezanim za zadatak 9.c)
neka je dan skup [latex]A[/latex] od [latex]n[/latex] elemenata. odredite koliko ima rastucih funkcija [latex]f:A\rightarrow A[/latex]
e sad, pretpostavljam da smijemo, bez smanjenja opcenitosti, uzeti [latex]A=\{1, 2,...,n\}[/latex], pa ce za svaku rastucu funkciju [latex]f:A\rightarrow A[/latex] vrijediti
[latex]i<j \Rightarrow f(i) \leq f(j)[/latex], pri cemu su [latex]i,j \in \{1, 2,...,n\}[/latex]
vidljivo je naprimjer da ako je, npr. [latex]f(2)=5[/latex], onda je nuzno [latex]f(3), f(4),...f(n) \in \{5,...,n\}[/latex],
odnosno [latex](f(i)=k) \Rightarrow f(j) \geq k[/latex], za [latex](i<j \leq n)[/latex]
ali ne znam kako ovo svojstvo icemu pomaze.
nemam pojma kako prebrojati sve rastuce funkcije sa [latex]A[/latex] u [latex]A[/latex] i bio bih izuzetno zahvalan na svakoj pomoci :D
evo, ja bih upao sa jednim drugim pitanjem, vezanim za zadatak 9.c)
neka je dan skup  od od  elemenata. odredite koliko ima rastucih funkcija elemenata. odredite koliko ima rastucih funkcija 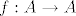
e sad, pretpostavljam da smijemo, bez smanjenja opcenitosti, uzeti 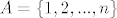 , pa ce za svaku rastucu funkciju , pa ce za svaku rastucu funkciju 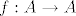 vrijediti vrijediti
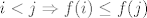 , pri cemu su , pri cemu su 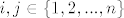
vidljivo je naprimjer da ako je, npr. 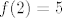 , onda je nuzno , onda je nuzno 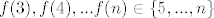 , ,
odnosno 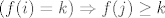 , za , za 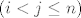
ali ne znam kako ovo svojstvo icemu pomaze.
nemam pojma kako prebrojati sve rastuce funkcije sa  u u  i bio bih izuzetno zahvalan na svakoj pomoci i bio bih izuzetno zahvalan na svakoj pomoci 
_________________  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 20:13 ned, 2. 11. 2008 Naslov: Postano: 20:13 ned, 2. 11. 2008 Naslov: |
    |
|
|
Nije bas jednostavno. Probaj prvo prebrojati strogo rastuce funkcije, laske je. Vise onako za zagrijavanje (nije od velike koristi za tvoj zadatak :) )
Za rastuce funkcije treba pogledati prirast u svakoj tocki: f(i)-f(i-1). Moze se napraviti bijekcija s necim sto se moze prebrojati pomocu "kuglica i stapica".
Sad sam primijetio da su domena i kodomena isti skup pa su strogo rastuce funkcije trivijala. Zadatak se inace moze rijesiti za f:{1,..,m}->{1,..,n}.
Nije bas jednostavno. Probaj prvo prebrojati strogo rastuce funkcije, laske je. Vise onako za zagrijavanje (nije od velike koristi za tvoj zadatak  ) )
Za rastuce funkcije treba pogledati prirast u svakoj tocki: f(i)-f(i-1). Moze se napraviti bijekcija s necim sto se moze prebrojati pomocu "kuglica i stapica".
Sad sam primijetio da su domena i kodomena isti skup pa su strogo rastuce funkcije trivijala. Zadatak se inace moze rijesiti za f:{1,..,m}->{1,..,n}.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 20:46 ned, 2. 11. 2008 Naslov: Postano: 20:46 ned, 2. 11. 2008 Naslov: |
    |
|
|
[quote="goranm"]A što točno je krivo postavljeno? :)[/quote]
pa pod (a) nam kaze da trebamo podijeliti zadatke ( nije nuzno da svaki student dobije zadatak ), tako da svaki od 30 zadataka dobije tocno jedan student, a pod (d) nam kaze da isto treba podijeliti zadatke( nije nuzno da svaki student dobije zadatak ), ali da niti jedan student ne smije dobiti dva ista zadatka?? pa zar mozemo iste zadatke dijeliti vise puta ako nam to i nije posebno napomenuto kao u (b)?
onda bi pod (a) imao beskonacno mnogo rjesenja, a pod (d) bi trebao moci podijeliti svakom studentu svih 30 zadatka, a i ne moram podijeliti ako ne zelim? pa bih molio objasnjenje... neznam dal se to samo meni događa, ali na svakoj zadaci ima jedan takav zadatak di trebam prvo dešifrirati dosta vremena na što se tu misli, a i kada rjesim zadatak nisam potpuno siguran dal je to tocno rjesenje jer nisam nikad siguran da li se baš to tražilo od mene.
| goranm (napisa): | A što točno je krivo postavljeno?  |
pa pod (a) nam kaze da trebamo podijeliti zadatke ( nije nuzno da svaki student dobije zadatak ), tako da svaki od 30 zadataka dobije tocno jedan student, a pod (d) nam kaze da isto treba podijeliti zadatke( nije nuzno da svaki student dobije zadatak ), ali da niti jedan student ne smije dobiti dva ista zadatka?? pa zar mozemo iste zadatke dijeliti vise puta ako nam to i nije posebno napomenuto kao u (b)?
onda bi pod (a) imao beskonacno mnogo rjesenja, a pod (d) bi trebao moci podijeliti svakom studentu svih 30 zadatka, a i ne moram podijeliti ako ne zelim? pa bih molio objasnjenje... neznam dal se to samo meni događa, ali na svakoj zadaci ima jedan takav zadatak di trebam prvo dešifrirati dosta vremena na što se tu misli, a i kada rjesim zadatak nisam potpuno siguran dal je to tocno rjesenje jer nisam nikad siguran da li se baš to tražilo od mene.
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 22:29 ned, 2. 11. 2008 Naslov: Postano: 22:29 ned, 2. 11. 2008 Naslov: |
    |
|
|
[quote="Cobs"][quote="goranm"]A što točno je krivo postavljeno? :)[/quote]
pa pod (a) nam kaze da trebamo podijeliti zadatke ( nije nuzno da svaki student dobije zadatak ), tako da svaki od 30 zadataka dobije tocno jedan student, a pod (d) nam kaze da isto treba podijeliti zadatke( nije nuzno da svaki student dobije zadatak ), ali da niti jedan student ne smije dobiti dva ista zadatka?? pa zar mozemo iste zadatke dijeliti vise puta ako nam to i nije posebno napomenuto kao u (b)?
[/quote]
I pod a) je napomenuto da ne smiješ iste zadatke dijeliti više puta različitim studentima (tj. piše da svaki zadatak mora dobiti točno jedan student).
Problem je u tome što napomena pod d) ("niti jedan student ne smije dobiti dva ista zadatka") sugerira da se, ako nije napomenuto drugačije, isti zadatak može dijeliti više puta jednom te istom studentu.
Zamisli da dođeš na test i dobiješ, lajk, beskonačno istih zadataka. :D
Ma mislim da je pod d) jednostavno neka greška.
| Cobs (napisa): | | goranm (napisa): | A što točno je krivo postavljeno?  |
pa pod (a) nam kaze da trebamo podijeliti zadatke ( nije nuzno da svaki student dobije zadatak ), tako da svaki od 30 zadataka dobije tocno jedan student, a pod (d) nam kaze da isto treba podijeliti zadatke( nije nuzno da svaki student dobije zadatak ), ali da niti jedan student ne smije dobiti dva ista zadatka?? pa zar mozemo iste zadatke dijeliti vise puta ako nam to i nije posebno napomenuto kao u (b)?
|
I pod a) je napomenuto da ne smiješ iste zadatke dijeliti više puta različitim studentima (tj. piše da svaki zadatak mora dobiti točno jedan student).
Problem je u tome što napomena pod d) ("niti jedan student ne smije dobiti dva ista zadatka") sugerira da se, ako nije napomenuto drugačije, isti zadatak može dijeliti više puta jednom te istom studentu.
Zamisli da dođeš na test i dobiješ, lajk, beskonačno istih zadataka. 
Ma mislim da je pod d) jednostavno neka greška.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
|
















