| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
krafnica
Forumaš(ica)

Pridružen/a: 21. 09. 2006. (20:50:28)
Postovi: (5F)16
Spol: 
|
|
| [Vrh] |
|
loreal
Forumaš(ica)


Pridružen/a: 09. 02. 2008. (18:30:35)
Postovi: (33)16
Spol: 
Lokacija: sava
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
zebrica
Forumaš(ica)
Pridružen/a: 06. 09. 2008. (09:22:46)
Postovi: (2F)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:32 sri, 4. 2. 2009 Naslov: Postano: 11:32 sri, 4. 2. 2009 Naslov: |
    |
|
|
Prvi zadatak pa fljos:
[b]O[/b] = Conv({[b]A[/b]0,...,[b]A[/b]k}) => simplex dim = k
[b]T[/b] E [b]O[/b]
Treba dokazati da je [b]O[/b]\{[b]T[/b]} konveksan akko [b]T[/b] E {[b]A[/b]0,...[b]A[/b]k}
Se smije ovako zaključivati:
=>
[b]T[/b] E {[b]A[/b]0,..,[b]A[/b]k} => [b]T[/b] = [b]A[/b]i, i E {0,...,k} => {[b]A[/b]o,...,[b]A[/b]i-1,[b]A[/b]i+1,...,[b]A[/b]k} lin. nez => [b]O[/b]\{[b]T[/b]} simplex dim=k-1 => [b]O[/b]\{[b]T[/b]} je stranica od [b]0[/b] => Konveksan
<=
[b]O[/b]\{[b]T[/b]} konveksan => ... e tu sad zapnem...
jel se može reći da je Conv({[b]T[/b]}) stranica od [b]O[/b] pa je stoga [b]T[/b] E {[b]A[/b]0,...[b]A[/b]k}?
A 2.?
Nije mi jasno, ako se traži da inf d(P,T) = 0 to ne znači da neka točka P nemože biti udaljena +beskonačno od T...
Prvi zadatak pa fljos:
O = Conv({A0,...,Ak}) ⇒ simplex dim = k
T E O
Treba dokazati da je O\{T} konveksan akko T E {A0,...Ak}
Se smije ovako zaključivati:
⇒
T E {A0,..,Ak} ⇒ T = Ai, i E {0,...,k} ⇒ {Ao,...,Ai-1,Ai+1,...,Ak} lin. nez ⇒ O\{T} simplex dim=k-1 ⇒ O\{T} je stranica od 0 ⇒ Konveksan
⇐
O\{T} konveksan ⇒ ... e tu sad zapnem...
jel se može reći da je Conv({T}) stranica od O pa je stoga T E {A0,...Ak}?
A 2.?
Nije mi jasno, ako se traži da inf d(P,T) = 0 to ne znači da neka točka P nemože biti udaljena +beskonačno od T...
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:58 sri, 4. 2. 2009 Naslov: Postano: 11:58 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="Saf"]{[b]A[/b]o,...,[b]A[/b]i-1,[b]A[/b]i+1,...,[b]A[/b]k} lin. nez => [b]O[/b]\{[b]T[/b]} simplex dim=k-1 => [b]O[/b]\{[b]T[/b]} je stranica od [b]0[/b] => Konveksan[/quote]
Ova prva implikacija baš i ne stoji. Ispalo bi da je trokut bez jednog vrha simplex dim 2, tj dužina :shock:
Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T}
| Saf (napisa): | | {Ao,...,Ai-1,Ai+1,...,Ak} lin. nez ⇒ O\{T} simplex dim=k-1 ⇒ O\{T} je stranica od 0 ⇒ Konveksan |
Ova prva implikacija baš i ne stoji. Ispalo bi da je trokut bez jednog vrha simplex dim 2, tj dužina 
Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T}
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:23 sri, 4. 2. 2009 Naslov: Postano: 12:23 sri, 4. 2. 2009 Naslov: |
    |
|
|
[code:1]{Ao,...,Ai-1,Ai+1,...,Ak} lin. nez => razapinju simplex? [/code:1]
To ne stoji? Jasna mi je paralela sa trokutom, ali... Jel stoji da je
[code:1]{T} = Conv(T) [/code:1]pa je:
[code:1]O/{T} = O/ Conv{T}?[/code:1]
A što ako za dužinu uzmem baš neku točku B i neki vrh Ai, onda se vrh nalazi na dužini koja je E od simplexsa, kaj ne? Npr. u trokutu ako uzmem dužinu AB, oba vrha su na dužini koja je E trokuta... Ili sam u krivu? Jel važan detalj PRAVA stranica od simpleksa i stranica od simplexa?
| Kod: | | {Ao,...,Ai-1,Ai+1,...,Ak} lin. nez => razapinju simplex? |
To ne stoji? Jasna mi je paralela sa trokutom, ali... Jel stoji da je
pa je:
A što ako za dužinu uzmem baš neku točku B i neki vrh Ai, onda se vrh nalazi na dužini koja je E od simplexsa, kaj ne? Npr. u trokutu ako uzmem dužinu AB, oba vrha su na dužini koja je E trokuta... Ili sam u krivu? Jel važan detalj PRAVA stranica od simpleksa i stranica od simplexa?
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:37 sri, 4. 2. 2009 Naslov: Postano: 14:37 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="Saf"][code:1]{Ao,...,Ai-1,Ai+1,...,Ak} lin. nez => razapinju simplex? [/code:1]
To ne stoji? [/quote]
To stoji. Ali taj simplex nije sigma\{T}, nego conv({A1..Ak}\{T})
Dakle, općenito [latex]conv(S \setminus \{T\}) \neq (conv(S)) \setminus \{T\}[/latex], za proizvoljan skup [latex]S[/latex]
Ili, strana simpleksa nije taj isti simpleks bez jedne točke.
| Saf (napisa): | | Kod: | | {Ao,...,Ai-1,Ai+1,...,Ak} lin. nez => razapinju simplex? |
To ne stoji? |
To stoji. Ali taj simplex nije sigma\{T}, nego conv({A1..Ak}\{T})
Dakle, općenito 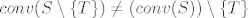 , za proizvoljan skup , za proizvoljan skup 
Ili, strana simpleksa nije taj isti simpleks bez jedne točke.
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 9:51 čet, 5. 2. 2009 Naslov: Postano: 9:51 čet, 5. 2. 2009 Naslov: |
    |
|
|
Jel može ovako:
O/{T} konveksan => T € {A0,...,Ak}
Daklem, pretpostavimo suprotno, tj:
[code:1]
T € O, T != {A0,...,Ak}, tada postoje A, B € O/{T}, i Lambda € R takvi da je (ABT)=Lambda
iz čega slijedi O/{T} nije konveksan (jer T !€ O/{T}) što se kosi s pretpostavkom...[/code:1]
[quote]Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T}
[/quote] Jel možeš to izvest molim te?
Jel može ovako:
O/{T} konveksan ⇒ T € {A0,...,Ak}
Daklem, pretpostavimo suprotno, tj:
| Kod: |
T € O, T != {A0,...,Ak}, tada postoje A, B € O/{T}, i Lambda € R takvi da je (ABT)=Lambda
iz čega slijedi O/{T} nije konveksan (jer T !€ O/{T}) što se kosi s pretpostavkom... |
| Citat: | Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T}
|
Jel možeš to izvest molim te?
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:19 čet, 5. 2. 2009 Naslov: Postano: 23:19 čet, 5. 2. 2009 Naslov: |
    |
|
|
[quote="Saf"][code:1]
T € O, T != {A0,...,Ak}, tada postoje A, B € O/{T}, i Lambda € R takvi da je (ABT)=Lambda[/code:1][/quote]
A odakle ti slijedi ovaj zaključak?? To i je poanta zadatka, da se to dokaže. Naravno da je intuitivno jasno da mora biti tako, al ne možeš baš tako uzeti.
[quote="Saf"][quote="rafaelm"]Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T} [/quote]Jel možeš to izvest molim te? [/quote]
Recimo da imamo lemu: [latex]T\in \sigma[/latex] je vrh akko ne postoje točke [latex]A,B \in \sigma \setminus \{T\}[/latex] td [latex]T\in \overline{AB}[/latex].
Neka su sada T neki vrh, te [latex]A,B \in \sigma \setminus \{T\}[/latex]. Tada je [latex]A,B \in \sigma[/latex], a [latex]\sigma[/latex] je konveksan,
pa je [latex]\overline{AB} \subset \sigma[/latex]. Ali po lemi, [latex]T\notin \overline{AB}[/latex], pa je [latex]\overline{AB} \subseteq \sigma \setminus \{T\}[/latex].
Pa slijedi da je [latex]\sigma \setminus \{T\}[/latex] konveksan.
Obratno, ako T nije vrh, tada po lemi postoje [latex]A,B \in \sigma \setminus \{T\}[/latex] td [latex]T \in \overline{AB}[/latex].
Znači [latex]\overline{AB} \nsubseteq \sigma \setminus \{T\}[/latex], pa [latex]\sigma \setminus \{T\}[/latex] nije konveksan skup.
Za dokazati lemu, treba postaviti koordinatni sustav, i koristiti analitički prikaz simpleksa kao skupa. ona suma, td zbroj koeficijenata bude 1, i svi su nenegativni. Neda mi se sve pisati, ima poprilično toga za naštimavati, al ovako ide skica.
Ako je T vrh, bez smanjenja općenitosti neka je [latex]T=A_{0}[/latex], a koordinatni sustav[latex](A_{0};\vec{A_{0}A_{1}},...,\vec{A_{0}A_{k}})[/latex]. Očito je tada [latex]T=(0,..,0)[/latex]. Neka je [latex]A \in \sigma \setminus \{T\}[/latex], pogledaj koje uvjete moraju zadovoljavati koordinate točke A. Neka je točka B, [latex]B \neq T[/latex], td [latex]T \in \overline{AB}[/latex], tj [latex]0=r_{T}=\lambda r_{A}+(1-\lambda) r_{B}[/latex], za neki [latex]\lambda \in <0,1>[/latex]. Pogledaj koje uvjete tada moraju zadovoljavati koordinate točke B. Pogledaj uvjete za biti u [latex]\sigma[/latex]. Vidit ćeš da[latex] B \notin \sigma[/latex].
Ako T nije vrh, stavim opet isti koordinatni sustav, ovajput [latex]T \neq (0,..,0)[/latex]. Stavim [latex]A:=A_{0}=(0,..,0) \in \sigma[/latex], [latex]B:=(\frac{t_{1}}{s},...,\frac{t_{k}}{s})[/latex], gdje je s suma koordinata točke T. Malo peljaš s nejednakostima i vidiš da je i [latex]B \in \sigma[/latex], pa je lema dokazana.
| Saf (napisa): | | Kod: |
T € O, T != {A0,...,Ak}, tada postoje A, B € O/{T}, i Lambda € R takvi da je (ABT)=Lambda |
|
A odakle ti slijedi ovaj zaključak?? To i je poanta zadatka, da se to dokaže. Naravno da je intuitivno jasno da mora biti tako, al ne možeš baš tako uzeti.
| Saf (napisa): | | rafaelm (napisa): | | Možeš dokazati npr. da se vrh ne može nalaziti na dužini AB, gdje su A,B € simplex. Pa iz toga lako slijedi konvexnost od simplex\{T} |
Jel možeš to izvest molim te? |
Recimo da imamo lemu: 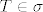 je vrh akko ne postoje točke je vrh akko ne postoje točke  td td  . .
Neka su sada T neki vrh, te  . Tada je . Tada je  , a , a  je konveksan, je konveksan,
pa je 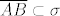 . Ali po lemi, . Ali po lemi,  , pa je , pa je 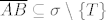 . .
Pa slijedi da je  konveksan. konveksan.
Obratno, ako T nije vrh, tada po lemi postoje  td td  . .
Znači  , pa , pa  nije konveksan skup. nije konveksan skup.
Za dokazati lemu, treba postaviti koordinatni sustav, i koristiti analitički prikaz simpleksa kao skupa. ona suma, td zbroj koeficijenata bude 1, i svi su nenegativni. Neda mi se sve pisati, ima poprilično toga za naštimavati, al ovako ide skica.
Ako je T vrh, bez smanjenja općenitosti neka je  , a koordinatni sustav , a koordinatni sustav . Očito je tada . Očito je tada 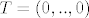 . Neka je . Neka je 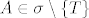 , pogledaj koje uvjete moraju zadovoljavati koordinate točke A. Neka je točka B, , pogledaj koje uvjete moraju zadovoljavati koordinate točke A. Neka je točka B, 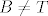 , td , td  , tj , tj  , za neki , za neki  . Pogledaj koje uvjete tada moraju zadovoljavati koordinate točke B. Pogledaj uvjete za biti u . Pogledaj koje uvjete tada moraju zadovoljavati koordinate točke B. Pogledaj uvjete za biti u  . Vidit ćeš da . Vidit ćeš da . .
Ako T nije vrh, stavim opet isti koordinatni sustav, ovajput 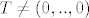 . Stavim . Stavim 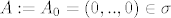 , , 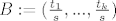 , gdje je s suma koordinata točke T. Malo peljaš s nejednakostima i vidiš da je i , gdje je s suma koordinata točke T. Malo peljaš s nejednakostima i vidiš da je i  , pa je lema dokazana. , pa je lema dokazana.
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|




















