| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 21:13 ned, 4. 1. 2009 Naslov: Postano: 21:13 ned, 4. 1. 2009 Naslov: |
    |
|
|
10b) podjeli sve sa najvećom potencijom, tj, sa n. onda dobiš:
lim [(sqrt(1+1/n)- 3.korijen(1-1/n)} = 1-1= 0
n u nulu u nulu
ovaj pod ce ti je na isti način.
btw dokad treba to predat'
10b) podjeli sve sa najvećom potencijom, tj, sa n. onda dobiš:
lim [(sqrt(1+1/n)- 3.korijen(1-1/n)} = 1-1= 0
n u nulu u nulu
ovaj pod ce ti je na isti način.
btw dokad treba to predat'
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Falva_Equa
Forumaš(ica)


Pridružen/a: 17. 11. 2008. (22:22:39)
Postovi: (8)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 11:44 uto, 6. 1. 2009 Naslov: Postano: 11:44 uto, 6. 1. 2009 Naslov: |
    |
|
|
šit, sad tek vidim da je topic 4. zadaća....... al, ček malo. otkud vama 4. zadaća?? na stranici je nema...........
šit, sad tek vidim da je topic 4. zadaća....... al, ček malo. otkud vama 4. zadaća?? na stranici je nema...........
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 12:04 uto, 6. 1. 2009 Naslov: Postano: 12:04 uto, 6. 1. 2009 Naslov: |
    |
|
|
al svejedno, jel taj deseti pod be i pod be ne treba samo podjelit najvećom potencijom i to je to??? rješenje pod be je nula, a pod ce je isto nula.
al svejedno, jel taj deseti pod be i pod be ne treba samo podjelit najvećom potencijom i to je to??? rješenje pod be je nula, a pod ce je isto nula.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Falva_Equa
Forumaš(ica)


Pridružen/a: 17. 11. 2008. (22:22:39)
Postovi: (8)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 17:11 sri, 7. 1. 2009 Naslov: Postano: 17:11 sri, 7. 1. 2009 Naslov: |
    |
|
|
e, jel mi može neko raspisati one sume iz 16-tog zadatka pod c) i pod d)? mislim, jedna je dosta, druga ide analogno. znam kako otprilike to izgleda, al ne znam matematički ispravno napisat kak to izgleda u raspisu. dođem do onog djela kad se treba izlučit n*n^2 i onda dalje ne znam kak da ovaj ostatak zapišem. mislim, imam neke ideje, al, neć se više blamirat neg što treba :)
e, jel mi može neko raspisati one sume iz 16-tog zadatka pod c) i pod d)? mislim, jedna je dosta, druga ide analogno. znam kako otprilike to izgleda, al ne znam matematički ispravno napisat kak to izgleda u raspisu. dođem do onog djela kad se treba izlučit n*n^2 i onda dalje ne znam kak da ovaj ostatak zapišem. mislim, imam neke ideje, al, neć se više blamirat neg što treba 
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 17:44 sri, 7. 1. 2009 Naslov: Postano: 17:44 sri, 7. 1. 2009 Naslov: |
    |
|
|
ček malo, pa jel nebi to trebalo stavit na treću, a onaj pod c) na drugu? il su to uopće i sasvim različiti izrazi za sumaciju?
ček malo, pa jel nebi to trebalo stavit na treću, a onaj pod c) na drugu? il su to uopće i sasvim različiti izrazi za sumaciju?
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:44 sri, 7. 1. 2009 Naslov: Postano: 22:44 sri, 7. 1. 2009 Naslov: |
    |
|
|
[quote="nlo"]Kuzim da se to indukcijom lagano pokaze, no ima li neki bolji/intuitivniji nacin?[/quote]
ima :)
Označimo [latex]S_n^k = 1^k + 2^k + \ldots + n^k[/latex], gdje je [latex]n[/latex] prirodan broj i [latex]k[/latex] prirodan broj ili [latex]0[/latex].
[latex]\left.\begin{array}{c@{\ =\ }l}
\left(0+1\right)^{k+1} & 0^{k+1} + {k+1 \choose 1} \cdot 0^k + {k+1 \choose 2} \cdot 0^{k-1} + \ldots + {k+1 \choose k} \cdot 0 + 1 \\
\left(1+1\right)^{k+1} & 1^{k+1} + {k+1 \choose 1} \cdot 1^k + {k+1 \choose 2} \cdot 1^{k-1} + \ldots + {k+1 \choose k} \cdot 1 + 1 \\
\left(2+1\right)^{k+1} & 2^{k+1} + {k+1 \choose 1} \cdot 2^k + {k+1 \choose 2} \cdot 2^{k-1} + \ldots + {k+1 \choose k} \cdot 2 + 1 \\
\vdots & \vdots
\\
\left(\left(n-1\right)+1\right)^{k+1} & \left(n-1\right)^{k+1} + {k+1 \choose 1} \cdot \left(n-1\right)^k + {k+1 \choose 2} \cdot \left(n-1\right)^{k-1} + \ldots + {k+1 \choose k} \cdot \left(n-1\right) + 1
\\
\left(n+1\right)^{k+1} & n^{k+1} + {k+1 \choose 1} \cdot n^k + {k+1 \choose 2} \cdot n^{k-1} + \ldots + {k+1 \choose k} \cdot n + 1
\end{array} \right\} +[/latex]
sada vidimo da općenito vrijedi da je
[latex]\left(n+1\right)^{k+1} = {k+1 \choose 1} S^k_n + {k+1 \choose 2} S^{k-1}_n + \ldots + {k+1 \choose k} S_n^1 + \left(n+1\right)[/latex], sada lako nalazimo da je
[latex]S_n^k = \frac{\left(n+1\right)^{k+1} - {k+1 \choose 2} S^{k-1}_n - \ldots - {k+1 \choose k} S_n^1 - S_n^0 - 1}{k+1}[/latex].
Znamo da je [latex]S_n^0 = n[/latex], zatim lako nalazimo
[latex]S_n^1 = \frac{\left(n+1\right)^2 - S_n^0 - 1}{2} = \frac{n\left(n+1\right)}{2}[/latex],
[latex]S_n^2 = \frac{\left(n+1\right)^3 - 3S_n^1 - S_n^0 - 1}{3} = \frac{n^3 + 3n^2 + 3n + 1 - \frac{3n\left(n+1\right)}{2} - n - 1}{3} = \frac{2n^3 + 3n^2 + n}{6} = \frac{n\left(n+1\right)\left(2n+1\right)}{6}[/latex],
[latex]S_n^3 = \frac{\left(n+1\right)^4 - 6S_n^2 - 4S_n^1 - S_n^0 -1}{4} = \frac{\left(n+1\right)^4 - n\left(n+1\right)\left(2n+1\right) - 2n\left(n+1\right) - \left(n+1\right)}{4} = \frac{\left(n+1\right)\left(n^3+3n^2+3n+1-2n^2-n-2n-1\right)}{4} =[/latex]
[latex]= \frac{n^2 \left(n+1\right)^2}{2^2} = \left(S_n^1\right)^2[/latex],
[latex]\vdots[/latex]
nadam se da sam barem nešto pomogao... :)
| nlo (napisa): | | Kuzim da se to indukcijom lagano pokaze, no ima li neki bolji/intuitivniji nacin? |
ima 
Označimo 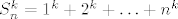 , gdje je , gdje je  prirodan broj i prirodan broj i  prirodan broj ili prirodan broj ili  . .
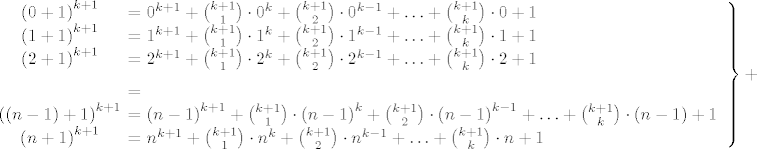
sada vidimo da općenito vrijedi da je
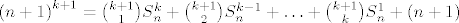 , sada lako nalazimo da je , sada lako nalazimo da je
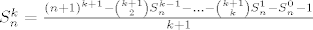 . .
Znamo da je 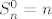 , zatim lako nalazimo , zatim lako nalazimo
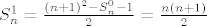 , ,
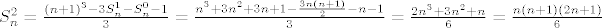 , ,
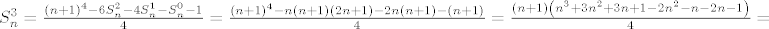
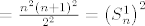 , ,

nadam se da sam barem nešto pomogao... 
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
|















