Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

limes
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
vriskica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
Sarma = la pohva - posuda
-10 = 7 - 17
PostPostano: 19:04 uto, 20. 1. 2009    Naslov: limes Citirajte i odgovorite
lim(x tezi beskonacno) [sin(1/x)+cos(1/x)]^x=
lim(x tezi beskonacno) [sin(1/x)+cos(1/x)]^x=


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 19:11 uto, 20. 1. 2009    Naslov: Citirajte i odgovorite
Pada mi sljedeća ideja...

Onaj x u exponentu napisat kao 2x/2 pa onda:

[latex][\sin{ \frac{1}{x}}+ \cos{\frac{1}{x}}]^x = [(\sin{ \frac{1}{x}}+ \cos{\frac{1}{x}})^2]^{\frac{x}{2}}[/latex]

Sad se zagrada kvadrira, ispadne 1+ sin(2/x) , a onda se limes sređuje na onaj oblik sa e-om :D
Pada mi sljedeća ideja...

Onaj x u exponentu napisat kao 2x/2 pa onda:



Sad se zagrada kvadrira, ispadne 1+ sin(2/x) , a onda se limes sređuje na onaj oblik sa e-om Very Happy



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vriskica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
Sarma = la pohva - posuda
-10 = 7 - 17
PostPostano: 20:05 sri, 21. 1. 2009    Naslov: Citirajte i odgovorite
kod mene ispalo e^beskonacno...de neka mi neko provjeri..

[size=9][color=#999999]Added after 1 hours 44 minutes:[/color][/size]

lim(x tezi beskonacno) [1+sin(2/x)]^(x/2)

L=e^l

l=lim(x tezi beskonacno) (x/2)[1+sin(2/x)-1]=
lim(x tezi beskonacno) (x/2)[sin(2/x)]=...

e sta sad dalje...pomozite.-.
kod mene ispalo e^beskonacno...de neka mi neko provjeri..

Added after 1 hours 44 minutes:

lim(x tezi beskonacno) [1+sin(2/x)]^(x/2)

L=e^l

l=lim(x tezi beskonacno) (x/2)[1+sin(2/x)-1]=
lim(x tezi beskonacno) (x/2)[sin(2/x)]=...

e sta sad dalje...pomozite.-.


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
nlo
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
Sarma = la pohva - posuda
0 = 6 - 6
PostPostano: 22:30 sri, 21. 1. 2009    Naslov: Citirajte i odgovorite
[latex](1+\sin{\frac{2}{x}})^{\frac{x}{2}}=(1+\frac{2}{x}+\mathcal{O}(\frac{1}{x^3}))^{\frac{x}{2}}[/latex], e sad ti zavrsi...
, e sad ti zavrsi...


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 23:19 sri, 21. 1. 2009    Naslov: Citirajte i odgovorite
Želimo namjestiti na oblik:

[latex]\lim_{x \to 0} { (1+x)^{\frac{1}{x}}}=e[/latex]

Ovdje imamo:

[latex]\lim_{x \to \infty} { (1+sin (\frac{2}{x}))^{\frac{x}{2}}}[/latex]

sad recimo supstitucija 2/x = t , pa kad x->besk, onda t->0 , pa je dalje ono gore

[latex]\lim_{t \to 0} { (1+sin t)^{\frac{1}{t}} = \lim_{t \to 0} { (1+sin t)^{\frac{1}{t} \cdot sint \cdot \frac{1}{sint}} = e^L[/latex]

gdje je

[latex]L=\lim_{t \to 0} { \frac{sint}{t}}= 1[/latex]
Rješenje je e^1 = e.

edit: moguće da je krivo al ja ne vidim grešku... imam feeling da bi trebalo +besk ispast...
Želimo namjestiti na oblik:



Ovdje imamo:



sad recimo supstitucija 2/x = t , pa kad x→besk, onda t→0 , pa je dalje ono gore



gdje je


Rješenje je e^1 = e.

edit: moguće da je krivo al ja ne vidim grešku... imam feeling da bi trebalo +besk ispast...



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
tperkov
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 12. 2008. (15:17:18)
Postovi: (71)16
Sarma = la pohva - posuda
8 = 14 - 6
PostPostano: 9:28 čet, 22. 1. 2009    Naslov: Citirajte i odgovorite
i l'Hospital kaže da je e, tako da dojam valjda vara
i l'Hospital kaže da je e, tako da dojam valjda vara


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 15:15 čet, 22. 1. 2009    Naslov: Citirajte i odgovorite
Dojam se bazirao na tom da sa u Mathematici išo to provjerit, pa mi je izbacivalo gluposti... a sve zato jer sam krivo prepiso zadatak... :oops:

Tako da je gornje rješenje dobro :D
Dojam se bazirao na tom da sa u Mathematici išo to provjerit, pa mi je izbacivalo gluposti... a sve zato jer sam krivo prepiso zadatak... Embarassed

Tako da je gornje rješenje dobro Very Happy



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vriskica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
Sarma = la pohva - posuda
-10 = 7 - 17
PostPostano: 15:29 pet, 23. 1. 2009    Naslov: limes Citirajte i odgovorite
lim(x tezi (pi/6)) [8sin^3(x)+1] / [2sin^2(x)-3sin(x)-2]
lim(x tezi (pi/6)) [8sin^3(x)+1] / [2sin^2(x)-3sin(x)-2]


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Anna Lee
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: žensko
Sarma = la pohva - posuda
2 = 11 - 9
Lokacija: Zagreb
PostPostano: 18:37 sub, 31. 1. 2009    Naslov: Citirajte i odgovorite
lim (n -> besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))

:cry:
lim (n -> besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))

Crying or Very sad


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Milojko
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
17 = 68 - 51
Lokacija: Hilbertov hotel
PostPostano: 9:41 ned, 1. 2. 2009    Naslov: Citirajte i odgovorite
možda nisam u pravu, ali mislim da znam:

opali prirodni logaritam na cijelu jednadžbu. onda zamjeni x sa jedan kroz x, to neka pomoćna varijabla t, i onda to ide u nulu. i onda kad se izračuna mislim da se dobije minus jedna polovina. al opet, nisam siguran, čini mi se da mi rješenje ima rupu
možda nisam u pravu, ali mislim da znam:

opali prirodni logaritam na cijelu jednadžbu. onda zamjeni x sa jedan kroz x, to neka pomoćna varijabla t, i onda to ide u nulu. i onda kad se izračuna mislim da se dobije minus jedna polovina. al opet, nisam siguran, čini mi se da mi rješenje ima rupu



_________________
Sedam je prost broj Smile

Bolonja je smeće i to pod hitno treba mijenjat
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 15:31 ned, 1. 2. 2009    Naslov: Citirajte i odgovorite
[quote="vriskica"]lim(x tezi (pi/6)) [8sin^3(x)+1] / [2sin^2(x)-3sin(x)-2][/quote]

Uvrstis li pi/6, imas
[latex]\frac{8 \sin^3 \pi/6+1}{2\sin^2 \pi/6 - 3 \sin \pi/6 - 2} = -\frac{2}{3}[/latex].
U cemu je problem? :grebgreb:

[quote="Anna Lee"]lim (n -> besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))[/quote]

Valjda x tezi u beskonacnost, a ne n. :-s I ono "e ^^ sin 2x" je vjerojatno "e ^ sin 2x". :) Uz te pretpostavke, primjecujem da je brojnik ogranicen (izmedju -e i e), a nazivnik nije, jer ocito tezi u
[latex]\infty(1-\infty) = -\infty[/latex],
pa bih - ovako napamet - rekao da je limes nula. :)
vriskica (napisa):
lim(x tezi (pi/6)) [8sin^3(x)+1] / [2sin^2(x)-3sin(x)-2]


Uvrstis li pi/6, imas
.
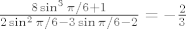U cemu je problem? Kotacici rade 100 na sat

Anna Lee (napisa):
lim (n → besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))


Valjda x tezi u beskonacnost, a ne n. Eh? I ono "e ^^ sin 2x" je vjerojatno "e ^ sin 2x". Smile Uz te pretpostavke, primjecujem da je brojnik ogranicen (izmedju -e i e), a nazivnik nije, jer ocito tezi u
,
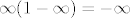pa bih - ovako napamet - rekao da je limes nula. Smile



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Anna Lee
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: žensko
Sarma = la pohva - posuda
2 = 11 - 9
Lokacija: Zagreb
PostPostano: 16:37 ned, 1. 2. 2009    Naslov: Citirajte i odgovorite
[quote="vsego"]

[quote="Anna Lee"]lim (n -> besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))[/quote]

Valjda x tezi u beskonacnost, a ne n. :-s I ono "e ^^ sin 2x" je vjerojatno "e ^ sin 2x". :) Uz te pretpostavke, primjecujem da je brojnik ogranicen (izmedju -e i e), a nazivnik nije, jer ocito tezi u
[latex]\infty(1-\infty) = -\infty[/latex],
pa bih - ovako napamet - rekao da je limes nula. :)[/quote]

hm da. obje pretpostavke su oke :lol:
ugl, uspjela sam ga rjesit jutros, onako uz formulice i dokazice, i isto sam dobila limes nula.
zahvaljujem puno. :)
vsego (napisa):


Anna Lee (napisa):
lim (n → besk) ((e^sin x) - (e^^ sin 2x))/((e^x) - (e^2x))


Valjda x tezi u beskonacnost, a ne n. Eh? I ono "e ^^ sin 2x" je vjerojatno "e ^ sin 2x". Smile Uz te pretpostavke, primjecujem da je brojnik ogranicen (izmedju -e i e), a nazivnik nije, jer ocito tezi u
,
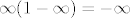pa bih - ovako napamet - rekao da je limes nula. Smile


hm da. obje pretpostavke su oke Laughing
ugl, uspjela sam ga rjesit jutros, onako uz formulice i dokazice, i isto sam dobila limes nula.
zahvaljujem puno. Smile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vriskica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
Sarma = la pohva - posuda
-10 = 7 - 17
PostPostano: 20:25 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
lim(x -> o+) (lnx)/(ctgx)
lim(x -> o+) (lnx)/(ctgx)


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 20:28 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
[quote="vriskica"]lim(x -> o+) (lnx)/(ctgx)[/quote]

L'hospital daje 0 ako se ne varam :D
vriskica (napisa):
lim(x → o+) (lnx)/(ctgx)


L'hospital daje 0 ako se ne varam Very Happy



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
tuv0k
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
Sarma = la pohva - posuda
3 = 5 - 2
PostPostano: 20:43 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
[latex]\lim_{n \to \ 0}\frac{ln(x)}{ctg(x)} = \lim_{n \to \ 0}\frac{- sin^2(x)}{x} = \lim_{n \to \ 0}\frac{-2sin(x)}{x} = 0[/latex]
valjda je to to... :)

valjda je to to... Smile



_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
vriskica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
Sarma = la pohva - posuda
-10 = 7 - 17
PostPostano: 20:55 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
lim(x -> beskon.) ((pi/2)-arc tgx)^(1/lnx)
lim(x -> beskon.) ((pi/2)-arc tgx)^(1/lnx)


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
tuv0k
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
Sarma = la pohva - posuda
3 = 5 - 2
PostPostano: 21:00 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
[quote="vriskica"]lim(x -> beskon.) ((pi/2)-arc tgx)^(1/lnx)[/quote]
Ovo nije forum za rješavanje zadataka :!:

Napiši do kuda si došla.
vriskica (napisa):
lim(x → beskon.) ((pi/2)-arc tgx)^(1/lnx)

Ovo nije forum za rješavanje zadataka Exclamation

Napiši do kuda si došla.



_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Luuka
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: muško
Sarma = la pohva - posuda
188 = 301 - 113
Lokacija: Hakuna Matata
PostPostano: 21:41 pon, 9. 2. 2009    Naslov: Citirajte i odgovorite
[quote="tuv0k"][latex]\lim_{n \to \ 0}\frac{ln(x)}{ctg(x)} = \lim_{n \to \ 0}\frac{- sin^2(x)}{x} = \lim_{n \to \ 0}\frac{-2sin(x)}{x} = 0[/latex]
valjda je to to... :)[/quote]

Nije baš...

[latex]\lim_{x \to \ 0}\frac{ln(x)}{ctg(x)} = \lim_{x \to \ 0}\frac{- sin^2(x)}{x} = \lim_{x \to \ 0}\frac{-2sin(x)cos(x)}{1} = 0[/latex]
ako ideš još jednim L'hospitalom, a može se iskoristit i da je lim (sinx/x) =1 pa ćeš imat -1*0 = 0 :D
tuv0k (napisa):

valjda je to to... Smile


Nije baš...


ako ideš još jednim L'hospitalom, a može se iskoristit i da je lim (sinx/x) =1 pa ćeš imat -1*0 = 0 Very Happy



_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy Very Happy
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan