|
[quote="PopStevo"]
vrijedi li isto ako je prostor elementarnih događaja neprebrojiv?
ne kužim zašto se profesor ograničio samo na prebrojive omege
hvala[/quote]
Izmjerivost funkcije definirane na skupu [latex]\Omega[/latex] nacelno nema nikakve veze sa mjerom definirano na tom skupu ( ako je uopce definirana ). Rijesimo dakle prvo pitanje izmjerivosti funkcije;
uoci da prilikom promatranja izmjerivosti funkcije uopce te ne zanima sta se dogada na njenoj kodomeni, zanima te sta se dogada sa orginalom tih skupova u kodomeni, jedan nacin da rijesis pitanje izmjerivosti, jest da za sigma algebru uzmes sve! A to sve je upravo partitivni skup domene ( provjeri da je to doista sigma algebra ), doista kakav god bio [latex]X^{-1}(A), A\subseteq \mathcal{F}[/latex] ( [latex]\mathcal{F}[/latex], sigma algebra na kodomeni ), on ce biti izmjeriv.
Primjeti da nigdje do sada nije bila spominjan kardinalitet skupa [latex]\Omega[/latex]. Dakle, isto vrijedi ukoliko je [latex]\Omega[/latex] neprebrojiv.
Jedan mali zadatak, pokazi da funkcija [latex]Y:\mathbb{R}\rightarrow \mathbb{R}[/latex], definirana sa [latex]Y(\omega)=\omega[/latex] ( veoma jednostavna, zar ne? ), nije izmjeriva ako je na domeni dana sljedeca sigma algebra [latex]\{\emptyset, \mathbb{R}\}[/latex], dakle trivijalna ( i ako ti se da, nadi koje su jedine izmjerive funkcije ).
Sada slijedi zahtjevan zadatak, izmjerivom prostoru [latex](\Omega,\mathcal{P}(\Omega))[/latex] zelimo dodati, po volji, mjeru. Obicno se navodi sljedeci primjer; uzme se [latex]\Omega=\mathbb{R}[/latex] te se za sigma algebru uzme [latex]\mathcal{P}(\mathbb{R})[/latex], te zelimo pridodati najprirodniju mjeru, a to je ona koja intervalu [latex][a,b][/latex] pridodaje njegovu duljnu [latex]b-a[/latex]. Vazna je sljedeca tvrdnja, a to je da ne postoji takva mjera ( malo sam izbjegao sve detalje sta se sve zahtjeva )! Dokaz ukljucuje "cjepanje" skupa realnih brojeva po skupu racionalnih, te primjenu aksioma izbora. Ti si konkretno pitao za vjerojatnost, uzmes [latex]([0,1],\mathcal{P}([0,1])[/latex], i slicno ne postoji vjerojatnost koja pridruzuje intervalu njegovu duljinu na spomenutoj sigma algebri.
I jos jedna napomena tehnickog karaktera, obicno se govori o izmjerivosti funkcije u [b]paru[/b] sigma algebri [latex](\mathcal{F},\mathcal{G})[/latex], gdje [latex]\mathcal{F}[/latex], sigma algebra na domeni, a [latex]\mathcal{G}[/latex], sigma algebra na kodomeni, naravno ako je jasno iz konteksta onda se obicno ne navodi.
| PopStevo (napisa): |
vrijedi li isto ako je prostor elementarnih događaja neprebrojiv?
ne kužim zašto se profesor ograničio samo na prebrojive omege
hvala |
Izmjerivost funkcije definirane na skupu 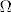 nacelno nema nikakve veze sa mjerom definirano na tom skupu ( ako je uopce definirana ). Rijesimo dakle prvo pitanje izmjerivosti funkcije; nacelno nema nikakve veze sa mjerom definirano na tom skupu ( ako je uopce definirana ). Rijesimo dakle prvo pitanje izmjerivosti funkcije;
uoci da prilikom promatranja izmjerivosti funkcije uopce te ne zanima sta se dogada na njenoj kodomeni, zanima te sta se dogada sa orginalom tih skupova u kodomeni, jedan nacin da rijesis pitanje izmjerivosti, jest da za sigma algebru uzmes sve! A to sve je upravo partitivni skup domene ( provjeri da je to doista sigma algebra ), doista kakav god bio 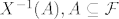 ( ( 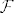 , sigma algebra na kodomeni ), on ce biti izmjeriv. , sigma algebra na kodomeni ), on ce biti izmjeriv.
Primjeti da nigdje do sada nije bila spominjan kardinalitet skupa 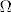 . Dakle, isto vrijedi ukoliko je . Dakle, isto vrijedi ukoliko je 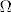 neprebrojiv. neprebrojiv.
Jedan mali zadatak, pokazi da funkcija 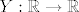 , definirana sa , definirana sa 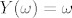 ( veoma jednostavna, zar ne? ), nije izmjeriva ako je na domeni dana sljedeca sigma algebra ( veoma jednostavna, zar ne? ), nije izmjeriva ako je na domeni dana sljedeca sigma algebra 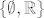 , dakle trivijalna ( i ako ti se da, nadi koje su jedine izmjerive funkcije ). , dakle trivijalna ( i ako ti se da, nadi koje su jedine izmjerive funkcije ).
Sada slijedi zahtjevan zadatak, izmjerivom prostoru 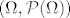 zelimo dodati, po volji, mjeru. Obicno se navodi sljedeci primjer; uzme se zelimo dodati, po volji, mjeru. Obicno se navodi sljedeci primjer; uzme se 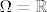 te se za sigma algebru uzme te se za sigma algebru uzme 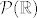 , te zelimo pridodati najprirodniju mjeru, a to je ona koja intervalu , te zelimo pridodati najprirodniju mjeru, a to je ona koja intervalu 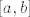 pridodaje njegovu duljnu pridodaje njegovu duljnu 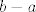 . Vazna je sljedeca tvrdnja, a to je da ne postoji takva mjera ( malo sam izbjegao sve detalje sta se sve zahtjeva )! Dokaz ukljucuje "cjepanje" skupa realnih brojeva po skupu racionalnih, te primjenu aksioma izbora. Ti si konkretno pitao za vjerojatnost, uzmes . Vazna je sljedeca tvrdnja, a to je da ne postoji takva mjera ( malo sam izbjegao sve detalje sta se sve zahtjeva )! Dokaz ukljucuje "cjepanje" skupa realnih brojeva po skupu racionalnih, te primjenu aksioma izbora. Ti si konkretno pitao za vjerojatnost, uzmes 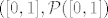 , i slicno ne postoji vjerojatnost koja pridruzuje intervalu njegovu duljinu na spomenutoj sigma algebri. , i slicno ne postoji vjerojatnost koja pridruzuje intervalu njegovu duljinu na spomenutoj sigma algebri.
I jos jedna napomena tehnickog karaktera, obicno se govori o izmjerivosti funkcije u paru sigma algebri 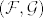 , gdje , gdje 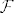 , sigma algebra na domeni, a , sigma algebra na domeni, a 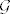 , sigma algebra na kodomeni, naravno ako je jasno iz konteksta onda se obicno ne navodi. , sigma algebra na kodomeni, naravno ako je jasno iz konteksta onda se obicno ne navodi.
|







