| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
glava
Forumaš(ica)

Pridružen/a: 28. 03. 2007. (18:48:16)
Postovi: (89)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:29 uto, 27. 1. 2009 Naslov: Postano: 14:29 uto, 27. 1. 2009 Naslov: |
    |
|
|
fx je derivacija po x gornje fje f(x,y). To se ispituje jer nas zanima dal u najvećem otv skupu (interioru) ima stac točaka, jer su i to kandidati za globalne extreme. Pošto nema, svi su extremi na rubu.
fx je derivacija po x gornje fje f(x,y). To se ispituje jer nas zanima dal u najvećem otv skupu (interioru) ima stac točaka, jer su i to kandidati za globalne extreme. Pošto nema, svi su extremi na rubu.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
glava
Forumaš(ica)

Pridružen/a: 28. 03. 2007. (18:48:16)
Postovi: (89)16
Spol: 
|
|
| [Vrh] |
|
lajka
Forumaš(ica)


Pridružen/a: 13. 02. 2008. (23:00:13)
Postovi: (39)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:57 pet, 30. 1. 2009 Naslov: Postano: 13:57 pet, 30. 1. 2009 Naslov: |
    |
|
|
[quote="lajka"]Moze li mi neko reci kako bi se trebao rjesit peti zadatak iz proslogodisnjeg kolokvija.. netriba mi sve, nego samo neki hint kako da krenem, zato jer nemam uopce ideje :(
zadatak glasi: Neka je f : R^n → R dva puta diferencijabilna sa svojstvom da je
D^2f(x) = 0, ∀x ∈ R^n.
Dokazite da tada postoje b ∈ R^n i c ∈ R takvi da vrijedi
f(x) = (b|x) + c, ∀x ∈ R^n.[/quote]
Otprilike, primjeniš teorem srednje vrijednosti na f-ju [latex]Df[/latex], [latex]Df(x)-Df(0)=D^{2}f(t)(x-0)=0[/latex]. Dakle, [latex]Df(x)=h, \ \forall x, \ h:=Df(0)[/latex], tj. prvi diferencijal je konstantna funkcija. Sad opet isto na funkciju [latex]f[/latex]: [latex]f(x)-f(0)=Df(s)(x-0)=h(x)[/latex]. Dakle [latex]f(x)=h(x)+a, \ \forall x, \ a:=f(0)[/latex], gdje je [latex]h[/latex] neki linearni funckional. Po onom teoremu o reprezentaciji linearnih funkcionala, postoji jedinstven vektor [latex]b[/latex] td [latex]h(x)=(b|x), \forall x[/latex]. Dakle [latex]f(x)=(b|x)+c, \forall x \in \mathbb{R}^{n}[/latex]
| lajka (napisa): | Moze li mi neko reci kako bi se trebao rjesit peti zadatak iz proslogodisnjeg kolokvija.. netriba mi sve, nego samo neki hint kako da krenem, zato jer nemam uopce ideje 
zadatak glasi: Neka je f : R^n → R dva puta diferencijabilna sa svojstvom da je
D^2f(x) = 0, ∀x ∈ R^n.
Dokazite da tada postoje b ∈ R^n i c ∈ R takvi da vrijedi
f(x) = (b|x) + c, ∀x ∈ R^n. |
Otprilike, primjeniš teorem srednje vrijednosti na f-ju 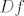 , , 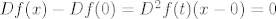 . Dakle, . Dakle, 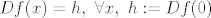 , tj. prvi diferencijal je konstantna funkcija. Sad opet isto na funkciju , tj. prvi diferencijal je konstantna funkcija. Sad opet isto na funkciju  : : 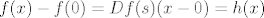 . Dakle . Dakle 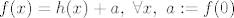 , gdje je , gdje je 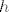 neki linearni funckional. Po onom teoremu o reprezentaciji linearnih funkcionala, postoji jedinstven vektor neki linearni funckional. Po onom teoremu o reprezentaciji linearnih funkcionala, postoji jedinstven vektor 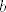 td td 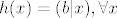 . Dakle . Dakle 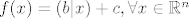
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
 Postano: 17:24 pon, 2. 2. 2009 Naslov: Postano: 17:24 pon, 2. 2. 2009 Naslov: |
    |
|
|
[quote="Luuka"]6.a) nakon razvoja u red na kraju imaš [latex]\frac{f^{(4)}(\alpha) x^4}{4!}[/latex] i to ti je ta greška, [color=red]valjda[/color]. (alfa je između x i 0) [/quote]
hm, da, i ja sam mislila da je to "nešto" u vezi toga, al ak ima netko tko bi mogo/znao to malo detaljnije objesnit, please :?
| Luuka (napisa): | 6.a) nakon razvoja u red na kraju imaš 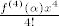 i to ti je ta greška, valjda. (alfa je između x i 0) i to ti je ta greška, valjda. (alfa je između x i 0) |
hm, da, i ja sam mislila da je to "nešto" u vezi toga, al ak ima netko tko bi mogo/znao to malo detaljnije objesnit, please 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
|














