| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
trashcan
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (00:09:47)
Postovi: (4)16
|
 Postano: 0:38 sub, 21. 2. 2009 Naslov: Diferencijalna jednadzba Postano: 0:38 sub, 21. 2. 2009 Naslov: Diferencijalna jednadzba |
    |
|
|
Ljudi ovako, uskoro mi je ispit, a ne znam kako se rjesava ovaj tip zadataka. Pokusao sam naci dokumentaciju i rjesene primjere za ovakve tipove zadataka, ali nije mi poslo za rukom, stoga Vas lijepo molim da mi netko ili korak po korak rjesi (pa bih sam skontao kako i zasto se to radi - ovom metodom sam substituciju savladao), ili linkom me uputi na sajt gdje bih to mogao naci.
Sve sto sam ja nasao nije mi pomoglo zbog:
a)mog nerazumjevanja matematickog jezika (gomila formula pokazuje nesto sto se tako jednostavno objasni na primjeru ili rijecima) :( :(
b) zadaci i rjesenja koje sam nasao na netu su mi nerazumljivi u tolikoj mjeri da mislim da nemaju veze sa ovim sto meni treba (racunanje povrsine itd itd)
Cini mi se da zadaci sami po sebi nisu teski (imamo profesora koji je jako uviđavan :D ) - ali postupak mi je nepoznat
Znaci, da ponovim, rjesenje korak po korak bi mi vise pomoglo od linka.
Evo zadatka :
[URL=http://img3.imageshack.us/my.php?image=123123tt6.png][img]http://img3.imageshack.us/img3/7851/123123tt6.th.png[/img][/URL]
iiii drugi ispit :) :
[URL=http://img21.imageshack.us/my.php?image=bezimenarj4.png][img]http://img21.imageshack.us/img21/8592/bezimenarj4.th.png[/img][/URL]
Evo ljudi, sto se mene tice, dovoljno je mi pomognete samo 3 zadatak, dovoljno mi je za prolaz (cetvrti se cini slozeniji, a ne bih Vas htio TOLIKO gnjaviti, ali ako se nekome da, bio bih zahvalan). U svoju obranu cu reci da studiram racunarstvo :) Hvala svima koji ce dati svoj doprinos da ovaj racunarac prođe zadnji kolegij iz matematike koji ce IKADA morati polagati :roll:
P.S. Nakon klikanja na thumbnail pojavi se malo veca verzija zadataka, no cini mi se da se ne vide dobro znakovi jednakosti i crta u razlomcima. Jos jedan klik na zadatke u novom prozoru Vas dovede do savrsene vidljivosti :)
Ljudi ovako, uskoro mi je ispit, a ne znam kako se rjesava ovaj tip zadataka. Pokusao sam naci dokumentaciju i rjesene primjere za ovakve tipove zadataka, ali nije mi poslo za rukom, stoga Vas lijepo molim da mi netko ili korak po korak rjesi (pa bih sam skontao kako i zasto se to radi - ovom metodom sam substituciju savladao), ili linkom me uputi na sajt gdje bih to mogao naci.
Sve sto sam ja nasao nije mi pomoglo zbog:
a)mog nerazumjevanja matematickog jezika (gomila formula pokazuje nesto sto se tako jednostavno objasni na primjeru ili rijecima)  
b) zadaci i rjesenja koje sam nasao na netu su mi nerazumljivi u tolikoj mjeri da mislim da nemaju veze sa ovim sto meni treba (racunanje povrsine itd itd)
Cini mi se da zadaci sami po sebi nisu teski (imamo profesora koji je jako uviđavan  ) - ali postupak mi je nepoznat ) - ali postupak mi je nepoznat
Znaci, da ponovim, rjesenje korak po korak bi mi vise pomoglo od linka.
Evo zadatka :

iiii drugi ispit  : :

Evo ljudi, sto se mene tice, dovoljno je mi pomognete samo 3 zadatak, dovoljno mi je za prolaz (cetvrti se cini slozeniji, a ne bih Vas htio TOLIKO gnjaviti, ali ako se nekome da, bio bih zahvalan). U svoju obranu cu reci da studiram racunarstvo  Hvala svima koji ce dati svoj doprinos da ovaj racunarac prođe zadnji kolegij iz matematike koji ce IKADA morati polagati Hvala svima koji ce dati svoj doprinos da ovaj racunarac prođe zadnji kolegij iz matematike koji ce IKADA morati polagati 
P.S. Nakon klikanja na thumbnail pojavi se malo veca verzija zadataka, no cini mi se da se ne vide dobro znakovi jednakosti i crta u razlomcima. Jos jedan klik na zadatke u novom prozoru Vas dovede do savrsene vidljivosti 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 0:58 sub, 21. 2. 2009 Naslov: Postano: 0:58 sub, 21. 2. 2009 Naslov: |
    |
|
|
Evo ovako, svi ovi zadaci idu na istu foru... dakle, tvoja tražena fja je y, koja je fja od x. ( dakle y' je deivacija y po x).
U svim ovim zadacima dano je koju supstituciju koristit...
[latex]y'-2x-2y=2[/latex] uz supstituciju u=x+y
jednadžbu se može napisati kao:
[latex]y'-2(x+y)=2[/latex] i tu vidimo naš u, još nam samo fali što je y'
iz supstitucije slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)
sve t uvrstimo nazad pa imamo:
[latex]u'-1-2u=2[/latex]
[latex]u'=2u+3[/latex]
ovo je jednadžba sa separiranim varijablama, koju je lako riješiti... naime podijlimo sve sa (2u+3) pa imamo:
[latex]\frac{u'}{2u+3}=1[/latex]
(pretpostavimo 2u+3!=0, u= -3/2 nam je trivijalno rješenje, vratit ćemo se tome kasnije)
integriranjem ovog imamo (sjetimo se, u je fja od x):
[latex]\int{\frac{u'}{2u+3}dx}=\int{1 dx}[/latex]
[latex] \frac{1}{2} \cdot ln|2u+3|=x+C[/latex]
gdje je C iz R proizvoljan (tj određen početnim uvjetom kojeg ovdje nema)
i sad nam preostaje vratit što je u pa imamo:
[latex] \frac{1}{2} \cdot ln|2(x+y)+3|=x+C[/latex]
ovo se može sredit da se dobije y= nešto, ali nije nužno.
To je naše rješenje...
još bi se trebalo napisati da je i u=-3/2 tj y= -3/2 -x također rješenje (ono trivijalno od gore)
u ostalim primjerima ideš potpuno isto, samo paziš kod deriviranja kad imaš u=x/y
iz tog je y=x/u pa je [latex]y'=\frac{u-xu'}{u^2}[/latex]
Evo ovako, svi ovi zadaci idu na istu foru... dakle, tvoja tražena fja je y, koja je fja od x. ( dakle y' je deivacija y po x).
U svim ovim zadacima dano je koju supstituciju koristit...
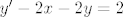 uz supstituciju u=x+y uz supstituciju u=x+y
jednadžbu se može napisati kao:
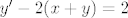 i tu vidimo naš u, još nam samo fali što je y' i tu vidimo naš u, još nam samo fali što je y'
iz supstitucije slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)
sve t uvrstimo nazad pa imamo:
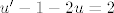
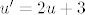
ovo je jednadžba sa separiranim varijablama, koju je lako riješiti... naime podijlimo sve sa (2u+3) pa imamo:
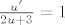
(pretpostavimo 2u+3!=0, u= -3/2 nam je trivijalno rješenje, vratit ćemo se tome kasnije)
integriranjem ovog imamo (sjetimo se, u je fja od x):
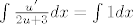
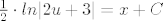
gdje je C iz R proizvoljan (tj određen početnim uvjetom kojeg ovdje nema)
i sad nam preostaje vratit što je u pa imamo:
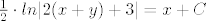
ovo se može sredit da se dobije y= nešto, ali nije nužno.
To je naše rješenje...
još bi se trebalo napisati da je i u=-3/2 tj y= -3/2 -x također rješenje (ono trivijalno od gore)
u ostalim primjerima ideš potpuno isto, samo paziš kod deriviranja kad imaš u=x/y
iz tog je y=x/u pa je 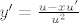
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
trashcan
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (00:09:47)
Postovi: (4)16
|
 Postano: 11:18 sub, 21. 2. 2009 Naslov: Postano: 11:18 sub, 21. 2. 2009 Naslov: |
    |
|
|
Ajme Luuka, hvala puno, odmah ujutro sam pogledao i ugodno se iznenadio. Ocekivao sam da cu odgovor dobiti tokom dana, ali ne odmah izjutra.
Da odgovorim na postavljeno pitanje, zadaci su iz ovogodisnjih ispitnih rokova. Znaaam, znaaam, svjestan sam da su lagani naspram onih kakve rade neki fakulteti i drugovi studenti - suosjecam sa Vama.
Ali kako su me ucili, poklonjenom konju ne gleda se u zube :wink:
[size=9][color=#999999]Added after 1 hours 34 minutes:[/color][/size]
E imam samo pitanje da vidim jesam li dobro skuzio...
Za vrijeme "slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)", znaci deriviram x^1, od tud je ova 1? Ili je "u" funkcija od "x" pa zbog tog umesto X pisem 1?
Nadalje,
[latex]
\int{\frac{u'}{2u+3}dx}=\int({{u'}*{\frac {1}{2u+3}dx}) =
\frac{1}{2} \cdot ln|2u+3|=x+C
[/latex]
Moze li mi netko pojasniti zasto se u' integrira kao
[latex]
\int{1^1}=\frac{1^2}{1+1}=\frac{1}{2}
[/latex]
tj. zasto u' dobiva vrijednost 1 prilikom integracije. Hvala
Luuka, jos jednom hvala, ako budem imao jos pitanja il nejasnoca, znam gdje se mogu javit. :D Ispit je u ponedjeljak-12:00 javim kak je proslo, hehehe
Ajme Luuka, hvala puno, odmah ujutro sam pogledao i ugodno se iznenadio. Ocekivao sam da cu odgovor dobiti tokom dana, ali ne odmah izjutra.
Da odgovorim na postavljeno pitanje, zadaci su iz ovogodisnjih ispitnih rokova. Znaaam, znaaam, svjestan sam da su lagani naspram onih kakve rade neki fakulteti i drugovi studenti - suosjecam sa Vama.
Ali kako su me ucili, poklonjenom konju ne gleda se u zube 
Added after 1 hours 34 minutes:
E imam samo pitanje da vidim jesam li dobro skuzio...
Za vrijeme "slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)", znaci deriviram x^1, od tud je ova 1? Ili je "u" funkcija od "x" pa zbog tog umesto X pisem 1?
Nadalje,
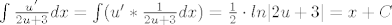
Moze li mi netko pojasniti zasto se u' integrira kao
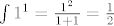
tj. zasto u' dobiva vrijednost 1 prilikom integracije. Hvala
Luuka, jos jednom hvala, ako budem imao jos pitanja il nejasnoca, znam gdje se mogu javit.  Ispit je u ponedjeljak-12:00 javim kak je proslo, hehehe Ispit je u ponedjeljak-12:00 javim kak je proslo, hehehe
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:43 sub, 21. 2. 2009 Naslov: Postano: 11:43 sub, 21. 2. 2009 Naslov: |
    |
|
|
[quote="trashcan"]
Za vrijeme "slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)", znaci deriviram x^1, od tud je ova 1? Ili je "u" funkcija od "x" pa zbog tog umesto X pisem 1?
Nadalje,
[latex]
\int{\frac{u'}{2u+3}dx}=\int({{u'}*{\frac {1}{2u+3}dx}) =
\frac{1}{2} \cdot ln|2u+3|=x+C
[/latex]
Moze li mi netko pojasniti zasto se u' integrira kao
[latex]
\int{1^1}=\frac{1^2}{1+1}=\frac{1}{2}
[/latex]
tj. zasto u' dobiva vrijednost 1 prilikom integracije. Hvala
[/quote]
jednadžbu deriviraš po x...
y=u-x -> y'=u'-1, to je zato jer je (y)'=y' , (u)'=u', (x)'=1. Ak kužiš kaj hoću reć...
a kod integrala ovaj u'=du/dx (derivacija u po x). Pa imaš integral
[latex]\int{\frac{du}{2u+3}}=\frac{1}{2} \cdot \int{\frac{2du}{2u+3}}=\frac{1}{2} \cdot ln|2u+3|[/latex]
(ako ne vidiš odmah možeš supstituciju z=2u+3 pa je dz=2du pa imaš
[latex]\frac{1}{2} \cdot \int{\frac{dz}{z}}[/latex]
a ona integracija od 1 ti je kriva... a i mislim da od gore kužiš zašto se u' ne integrira ko 1 :D
inače, integral od 1db je b, kaj god pisalo za b. :D
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
E da, kod onih drugih zadataka imaš u=y/x pa je y=xu iz čega slijedi da je y'=xu'+u
ja sam u prvom postu napiso za u=x/y, krivo sam prepiso :D
| trashcan (napisa): |
Za vrijeme "slijedi da je y=u-x pa je y'=u'-1 (u je isto fja od x)", znaci deriviram x^1, od tud je ova 1? Ili je "u" funkcija od "x" pa zbog tog umesto X pisem 1?
Nadalje,
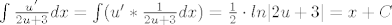
Moze li mi netko pojasniti zasto se u' integrira kao
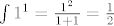
tj. zasto u' dobiva vrijednost 1 prilikom integracije. Hvala
|
jednadžbu deriviraš po x...
y=u-x → y'=u'-1, to je zato jer je (y)'=y' , (u)'=u', (x)'=1. Ak kužiš kaj hoću reć...
a kod integrala ovaj u'=du/dx (derivacija u po x). Pa imaš integral
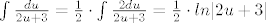
(ako ne vidiš odmah možeš supstituciju z=2u+3 pa je dz=2du pa imaš
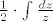
a ona integracija od 1 ti je kriva... a i mislim da od gore kužiš zašto se u' ne integrira ko 1 
inače, integral od 1db je b, kaj god pisalo za b. 
Added after 9 minutes:
E da, kod onih drugih zadataka imaš u=y/x pa je y=xu iz čega slijedi da je y'=xu'+u
ja sam u prvom postu napiso za u=x/y, krivo sam prepiso 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
trashcan
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (00:09:47)
Postovi: (4)16
|
 Postano: 11:57 sub, 21. 2. 2009 Naslov: Postano: 11:57 sub, 21. 2. 2009 Naslov: |
    |
|
|
Hehehe, hvala majstore, sad mogu rec da mi je jasno sve... eh, supstitucija... i vidi vraga dobro ispadne! :D
Drzat cu se onih - ne postoje glupa pitanja, samo glupi ljudi :oops: , pa se jos javim ako zapnem.
Evooo, zapeooooooo... rjesavam 3. zadatak iz prbog thumbnaila.
Znaci,
1. [latex]
u = x+y+1
[/latex]
2. [latex]
y=u-x-1
[/latex]
3. [latex]
y'=u'-1
[/latex]
4. [latex]
\frac{1}{u} + y'=u /:u
[/latex]
5. [latex]
\int{\frac{u'-1}{u^2}dx}= x + C
[/latex]
I sad nemam poooooojma kako ovo integrirat :(
Hehehe, hvala majstore, sad mogu rec da mi je jasno sve... eh, supstitucija... i vidi vraga dobro ispadne! 
Drzat cu se onih - ne postoje glupa pitanja, samo glupi ljudi  , pa se jos javim ako zapnem. , pa se jos javim ako zapnem.
Evooo, zapeooooooo... rjesavam 3. zadatak iz prbog thumbnaila.
Znaci,
1. 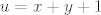
2. 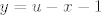
3. 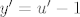
4. 
5. 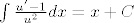
I sad nemam poooooojma kako ovo integrirat 
|
|
| [Vrh] |
|
trashcan
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (00:09:47)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|







