zadatak sa particijama

[Anna Lee]

Neka je S skup te neka su F i G particije skupa S sa sljedecim svojstvima:
1. za svaki A element F postoji B element G takav da je A nadskup od B
2. za svaki B element G postoji A element F takav da je B nadskup od A.
Mora li tada vrijediti F = G? Svoj odg. obrazlozite.

pliz, ak bi netko to znao dokazat nek mi pomogne...

_________________
"The tooth fairy teaches children that they can sell body parts for money."

[tomitza]

aha, taj je zadatak bio u prvom kolokviju... sjecam ga se...

uzmes neki A1 iz F. Po prvom uvjetu, postoji B1 iz G takava da je A1<=B1.

sad opet uzmes taj B1 iz G i onda iz drugog uvjeta ti slijedi da postoji A2 iz F takav da je B1<=A2.

i sada imas situaciju A1<=B1<=A2. Posto su A1 i A2 "komadi"(nije bas mat. izraz, al nije bitno) particije istog skupa, nuzno je da su disjunktni, a u ovom slucaju, ti imas da je A2 nadskup A1. Jedina moguca opcija je da je A1=A2, sto povlaci A1=B1, sto opet povlaci da su particije F i G jednake... Q.E.D.

nap. ovo (<=) nije znak usporedbe brojeva nego skupova, al to nije toliko bitno, bitno je da skuzis poantu...

_________________
http://catenary.files.wordpress.com/2007/10/if_youre_happy_and_you_know_it.jpg

[Anna Lee]

ahaaaaa, skuzila sam. hvala puno

_________________
"The tooth fairy teaches children that they can sell body parts for money."

[Anna Lee]

ovaaaaaj...opet ja. vise nisu particije, al necu otvarat nocu temu.

Odredite sve polinome p element R[x] stupnja najvise 2 takve da je p(x^2)=(p(x))^2, za svaki x iz skupa R.

kak se rjesavaju ovakvi zadaci? ne znam ih ni zapocet.

_________________
"The tooth fairy teaches children that they can sell body parts for money."

[Luuka]

Koristiš tm o jednakosti polinoma... on kaže da su dva polinoma jednaka ako su istog stupnja i ako su koeficijenti uz svaku potenciju jednaki.

kod tebe je polinom p oblika: p(x)=ax^2 + bx +c za neke a,b,c iz R.

uvjet p(x^2)=(p(x))^2 daje:



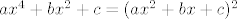
ovo desno kvadriraš, izjednačiš koef uz iste potencije i dobiješ uvjete na a,b,c

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[Anna Lee]

zahvaljujem

_________________
"The tooth fairy teaches children that they can sell body parts for money."

[indexnet]

jeli mi može netko reći kako da riješim:
1. Odredite koeficijent a iz R f (x) = x3 - 3 x2 + ax + 1 tako da nultočke polinoma zadovoljavaju jednakost x1^2 + x2^2 + x3^2=21/4. odredi koje su to nultočke?

2. odrediti mjeru (3^4102 - 3^2113, 3^4105 - 3^2113)?

[markotron]

1. zadatak.. rijesis pomocu vietovih formula..

x1^2 + x2^2 + x3^2=21/4

x1^2 + x2^2 + x3^2= (x1 + x2 + x3)^2 - (x1x2 + x2x3 + x1x3)

(x1 + x2 + x3), (x1x2 + x2x3 + x1x3) znas koliko iznose.. izjednacis to sa 21/4.. i dobijes rjesenje.. nultocke kasnije lako nadjes..

2. zadatak.. mozes ispred zagrade izlcuit 3^2113.. i onda sablonski rijesis (identicno kao na vjezbam)

_________________
reductio ad absurdum