Ostao sam duzan alternativna [url=http://xkcd.com/199/]"pravila desne ruke"[/url] i formulu za racunanje vektorskog produkta. Neka je [latex]\{\vec i, \vec j, \vec k\}[/latex] ortonormirana baza vektorskog prostora [latex]V^3[/latex] u kojoj vektori [latex]\vec a[/latex], [latex]\vec b[/latex] imaju koordinate [latex](\alpha_1, \alpha_2, \alpha_3)[/latex] i [latex](\beta_1, \beta_2, \beta_3)[/latex] (tj. [latex]\vec a = \alpha_1 \vec i + \alpha_2 \vec j + \alpha_3 \vec k[/latex] i analogno za [latex]\vec b[/latex]). Onda vektorski produkt mozemo izracunati razvojem sljedece "determinante" po prvom retku:
[latex]\vec a \times \vec b = \left| \begin{array}{ccc}
\vec i & \vec j & \vec k\\
\alpha_1 & \alpha_2 & \alpha_3\\
\beta_1 & \beta_2 & \beta_3\\
\end{array}\right| =
\left|\begin{array}{cc}
\alpha_2 & \alpha_3\\
\beta_2 & \beta_3\\
\end{array}\right| \vec i
- \left|\begin{array}{cc}
\alpha_1 & \alpha_3\\
\beta_1 & \beta_3\\
\end{array}\right| \vec j
+ \left|\begin{array}{cc}
\alpha_1 & \alpha_2\\
\beta_1 & \beta_2\\
\end{array}\right| \vec k.
[/latex]
Hoce se reci da vektorski produkt u istoj bazi ima sljedece koordinate, koje cete najlakse zapamtiti preko gornje 3x3 kvazideterminante:
[latex](\alpha_2 \beta_3 - \alpha_3 \beta_2,
\alpha_3 \beta_1 - \alpha_1 \beta_3,
\alpha_1 \beta_2 - \alpha_2 \beta_1).[/latex]
Ostao sam duzan alternativna "pravila desne ruke" i formulu za racunanje vektorskog produkta. Neka je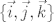 
ortonormirana baza vektorskog prostora 
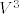u kojoj vektori 
, 
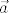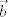imaju koordinate 
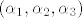i 
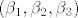(tj.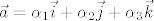 
i analogno za 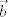). Onda vektorski produkt mozemo izracunati razvojem sljedece "determinante" po prvom retku:
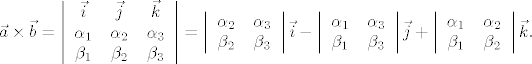
Hoce se reci da vektorski produkt u istoj bazi ima sljedece koordinate, koje cete najlakse zapamtiti preko gornje 3x3 kvazideterminante:
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
