| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 19:30 čet, 4. 9. 2008 Naslov: grupa automorfizama Postano: 19:30 čet, 4. 9. 2008 Naslov: grupa automorfizama |
    |
|
|
u pitanju je gradivo algebre ali pišem ovdje jer ću tu valjda lakše naći stručnjake :)
dakle muče me zadaci tipa "odredi grupu Aut(Z_n)" za neki n... primjeri iz vježbi su dosta jednostavni a ja još nekako nisam "na ti" sa cijelom pričom pa molim pomoć.
npr. Aut(Z_20). znači tražim sve endomorfizme [latex]\phi[/latex] takve da [latex]\langle\phi(1)\rangle=Z_{20}[/latex], tj. preslikavaju jedinicu u generator. generatori u [latex]Z_{20}[/latex] su brojevi 1, 3, 7, 9, 11, 13, 17, 19. Ima ih 8, dakle tražena grupa automorfizama je reda 8. super! ali koja?
promatram redove preslikavanja, uz oznaku [latex]\phi_{i}(1)=i[/latex].
otkrijem da imam 4 elementa reda 4 i 3 reda 2. je li to sad znači da je [latex]Aut(Z_{20}) = Z_2\times Z_4[/latex] (ne mogu nać znak za izomorfizam)? ili ne? kada (i zbog čega) mogu biti sto posto sigurna da sam našla pravu grupu?
u pitanju je gradivo algebre ali pišem ovdje jer ću tu valjda lakše naći stručnjake 
dakle muče me zadaci tipa "odredi grupu Aut(Z_n)" za neki n... primjeri iz vježbi su dosta jednostavni a ja još nekako nisam "na ti" sa cijelom pričom pa molim pomoć.
npr. Aut(Z_20). znači tražim sve endomorfizme 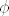 takve da takve da 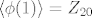 , tj. preslikavaju jedinicu u generator. generatori u , tj. preslikavaju jedinicu u generator. generatori u 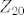 su brojevi 1, 3, 7, 9, 11, 13, 17, 19. Ima ih 8, dakle tražena grupa automorfizama je reda 8. super! ali koja? su brojevi 1, 3, 7, 9, 11, 13, 17, 19. Ima ih 8, dakle tražena grupa automorfizama je reda 8. super! ali koja?
promatram redove preslikavanja, uz oznaku 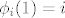 . .
otkrijem da imam 4 elementa reda 4 i 3 reda 2. je li to sad znači da je 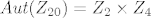 (ne mogu nać znak za izomorfizam)? ili ne? kada (i zbog čega) mogu biti sto posto sigurna da sam našla pravu grupu? (ne mogu nać znak za izomorfizam)? ili ne? kada (i zbog čega) mogu biti sto posto sigurna da sam našla pravu grupu?
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:21 pon, 25. 5. 2009 Naslov: Postano: 16:21 pon, 25. 5. 2009 Naslov: |
    |
|
|
Zadatak je slijedeći: da li je grupa [latex]Aut(\mathbb{Z}_2 \oplus \mathbb{Z}_2)[/latex] ciklička?
Moj pokušaj rješenja: Za svaki [latex]f \in Aut(\mathbb{Z}_2 \oplus \mathbb{Z}_2)[/latex] mora vrijediti [latex]f((0,0))=(0,0)[/latex] jer je f endomorfizam pa mora preslikavat neutralni element u neutralni. Ostaje za odrediti u što će f preslikati preostala 3 elementa. Kako f mora biti injekcija, te elemente možemo raspodijeliti na 3!=6 načina, i to su slijedeća preslikavanja:
[latex]\left(\begin{array}{ccc}
1 & 2 & 3 \\
1 & 2 & 3
\end{array}\right)\quad\left(\begin{array}{ccc}
1 & 2 & 3 \\
1 & 3 & 2
\end{array}\right)\quad\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 1 & 3
\end{array}\right)\quad\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right)\quad
\left(\begin{array}{ccc}
1 & 2 & 3 \\
3 & 1 & 2
\end{array}\right)\quad
\left(\begin{array}{ccc}
1 & 2 & 3 \\
3 & 2 & 1
\end{array}\right)\quad,
[/latex]
gdje je [latex]1 \sim (0,1)[/latex], [latex]2 \sim (1,0)[/latex] i [latex]3 \sim (1,1)[/latex].
Lako se provjeri da svih 6 jesu endomorfizmi pa su i automorfizmi.
Kada bi [latex]Aut(\mathbb{Z}_2 \oplus \mathbb{Z}_2)[/latex] bila ciklička, tada bi morala biti i abelova, no kako je
[latex]\left(\begin{array}{ccc}
1 & 2 & 3 \\
1 & 3 & 2
\end{array}\right)
\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 1 & 3
\end{array}\right)=\left(\begin{array}{ccc}
1 & 2 & 3 \\
3 & 1 & 2
\end{array}\right)\\[/latex]
[latex]
\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 1 & 3
\end{array}\right)
\left(\begin{array}{ccc}
1 & 2 & 3 \\
1 & 3 & 2
\end{array}\right)=\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right)
[/latex]
tada [latex]Aut(\mathbb{Z}_2 \oplus \mathbb{Z}_2)[/latex] nije abelova pa ne može biti ciklička.
Moja pitanja: da li je rješenje ispravno, a ako je (i ako nije :lol:), postoji li neki elegantniji način da se to riješi? :)
Zadatak je slijedeći: da li je grupa 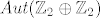 ciklička? ciklička?
Moj pokušaj rješenja: Za svaki 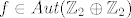 mora vrijediti mora vrijediti  jer je f endomorfizam pa mora preslikavat neutralni element u neutralni. Ostaje za odrediti u što će f preslikati preostala 3 elementa. Kako f mora biti injekcija, te elemente možemo raspodijeliti na 3!=6 načina, i to su slijedeća preslikavanja: jer je f endomorfizam pa mora preslikavat neutralni element u neutralni. Ostaje za odrediti u što će f preslikati preostala 3 elementa. Kako f mora biti injekcija, te elemente možemo raspodijeliti na 3!=6 načina, i to su slijedeća preslikavanja:
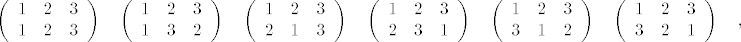
gdje je 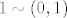 , , 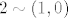 i i 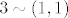 . .
Lako se provjeri da svih 6 jesu endomorfizmi pa su i automorfizmi.
Kada bi 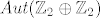 bila ciklička, tada bi morala biti i abelova, no kako je bila ciklička, tada bi morala biti i abelova, no kako je
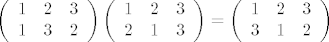
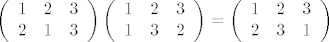
tada 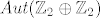 nije abelova pa ne može biti ciklička. nije abelova pa ne može biti ciklička.
Moja pitanja: da li je rješenje ispravno, a ako je (i ako nije  ), postoji li neki elegantniji način da se to riješi? ), postoji li neki elegantniji način da se to riješi? 
_________________
The Dude Abides
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
|










