| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
amorphis
Forumaš(ica)
Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
 Postano: 23:23 pon, 15. 6. 2009 Naslov: nejasnoća u vezi zadatka |
    |
|
|
treba mi pomoć za prošlogodišnji drugi kolokvij (Zd 4b)
jasno mi je kako se sredi matrica, jasno mi je kako se izračuna determinanta, ali ne razumijem kako se dobije podintegralna funkcija u predzadnjem redu; 6 ostaje 6 jer je konstanta, (v-u) je tu zbog determinante, ali nije mi jasno kako 'z' postaje 'uv'?
(ps - znam da bi se trebao copy/paste dio zadatka, ali kad to napravim dobijem samo hrpu nečitljivih znakova, pa moram ovako)
treba mi pomoć za prošlogodišnji drugi kolokvij (Zd 4b)
jasno mi je kako se sredi matrica, jasno mi je kako se izračuna determinanta, ali ne razumijem kako se dobije podintegralna funkcija u predzadnjem redu; 6 ostaje 6 jer je konstanta, (v-u) je tu zbog determinante, ali nije mi jasno kako 'z' postaje 'uv'?
(ps - znam da bi se trebao copy/paste dio zadatka, ali kad to napravim dobijem samo hrpu nečitljivih znakova, pa moram ovako)
_________________
We strongly recommend using Firefox to fully enjoy this site.
|
|
| [Vrh] |
|
Sphiro
Forumaš(ica)
Pridružen/a: 17. 10. 2007. (16:32:45)
Postovi: (45)16
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)
Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Ally
Forumaš(ica)
Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol:
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)
Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
| Postano: 11:13 ned, 28. 6. 2009 Naslov: |
|
|
|
Joooj tu ima samo puno raspisivanja...
Napiši po definiciji Darbouxove sume na zadanoj subdiviziji.
Unutar dvostruke sume ćeš imat površinu pravokutnika, kaj će uvijek bit 1/n * 1/n = 1/n^2, a maximum/minimum fje će bit u nekom od vrhova pravokutnika.
Maximum će biti u bilo kojoj točki na donjoj stranici pravokutnika ( za y=1/i jer je f(1/i)= 1 + 1/i> 1+ 1/(i+1)=f( 1/(i+1) ) )
Za minimum slično, samo uzmeš onaj drugi rub.
Izračunaš obje sume, to bi trebalo bit lako, onda limes po n od njih. Trebalo bi ispast isto :D
Za onu finiju particiju (kad ide na 2n dijelova) opet isto, samo kaj ćeš sad imat više točaka... i vrijednost sume će se približit limesu :D
Joooj tu ima samo puno raspisivanja...
Napiši po definiciji Darbouxove sume na zadanoj subdiviziji.
Unutar dvostruke sume ćeš imat površinu pravokutnika, kaj će uvijek bit 1/n * 1/n = 1/n^2, a maximum/minimum fje će bit u nekom od vrhova pravokutnika.
Maximum će biti u bilo kojoj točki na donjoj stranici pravokutnika ( za y=1/i jer je f(1/i)= 1 + 1/i> 1+ 1/(i+1)=f( 1/(i+1) ) )
Za minimum slično, samo uzmeš onaj drugi rub.
Izračunaš obje sume, to bi trebalo bit lako, onda limes po n od njih. Trebalo bi ispast isto 
Za onu finiju particiju (kad ide na 2n dijelova) opet isto, samo kaj ćeš sad imat više točaka... i vrijednost sume će se približit limesu
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
lucika
Forumaš(ica)
Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 22:13 ned, 30. 8. 2009 Naslov: |
|
|
|
Ja naravno zeznuo :oops:
Ali princip je sličan... fja nam je f(x,y)=y+1 pa će maximum biti na gornjoj stranici pravokutnika.
Sad (nakon izlučivanja) imamo
[latex]S(f, P^n)= \frac{1}{n^2} \sum_i \sum_j max(f, P_{i,j})[/latex]
taj maximum se postiže na gornjem rubu pravokutnika Pij ( [(i-1)/n,i/n]x[(j-1)/n,j/n] ) pa dobijemo:
[latex]S(f, P^n)= \frac{1}{n^2} \sum_i \sum_j (j+1) =\frac{1}{n^2} \sum_i ( \sum_{j=1}^{n} \frac{j}{n} + n) = [/latex]
[latex]= \frac{1}{n^2} \cdot n \cdot ( \frac{n+1}{2} + n) = \frac{3n+1}{2n}[/latex]
a limes toga je 3/2.
( a integral je isto toliki :D )
Ja naravno zeznuo 
Ali princip je sličan... fja nam je f(x,y)=y+1 pa će maximum biti na gornjoj stranici pravokutnika.
Sad (nakon izlučivanja) imamo
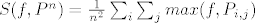
taj maximum se postiže na gornjem rubu pravokutnika Pij ( [(i-1)/n,i/n]x[(j-1)/n,j/n] ) pa dobijemo:
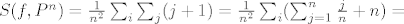
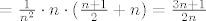
a limes toga je 3/2.
( a integral je isto toliki )
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
lucika
Forumaš(ica)
Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol:
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 20:05 pon, 31. 8. 2009 Naslov: |
|
|
|
To bi bila ona veća stranica tog "kvadra"... graf te fje bi izgledo ovak:
[img]http://www.imagesforme.com/out.php/i666414_untitled.JPG[/img]
to je graf nad pravokutnikom [0,1]x[0,1], dakle kvadar s time da je nakošen gore... i maximum je na stranici od (0,1) do (1,1).
(nacrtaj si još u 2D pravokutnik pa kak ide y+1 iznad)
To bi bila ona veća stranica tog "kvadra"... graf te fje bi izgledo ovak:
to je graf nad pravokutnikom [0,1]x[0,1], dakle kvadar s time da je nakošen gore... i maximum je na stranici od (0,1) do (1,1).
(nacrtaj si još u 2D pravokutnik pa kak ide y+1 iznad)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
|
