| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
oblak24
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (20:48:46)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 19:40 sri, 19. 8. 2009 Naslov: Postano: 19:40 sri, 19. 8. 2009 Naslov: |
    |
|
|
Oznacimo sumu za n:
[latex]S_n := \sum_{k=1}^{2n} (-1)^{k+1} k^3[/latex]
Za n+1:
[latex]$\begin{align*}S_{n+1} &= \sum_{k=1}^{2(n+1)} (-1)^{k+1} k^3 = \sum_{k=1}^{2n} (-1)^{k+1} k^3 + (-1)^{(2n+1)+1} (2n+1)^3 + (-1)^{(2n+2)+1} (2n+2)^3 \\
&= S_n + (-1)^{(2n+1)+1} (2n+1)^3 + (-1)^{(2n+2)+1} (2n+2)^3.
\end{align*}$[/latex]
Dakle, nova suma ima dva elementa vise, pa ih "izvadimo" van i onda nam ostane "suma za prvih n elemenata plus ta dva viska". 8)
Dalje je lako: uvrstis pretpostavku indukcije i sredis; trebas dobiti
[latex]-(n+1)^2(4(n+1)+3)[/latex]. :)
Jos ti ostane baza indukcije (za n=1), no to je trivijalno. 8)
Oznacimo sumu za n:
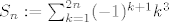
Za n+1:
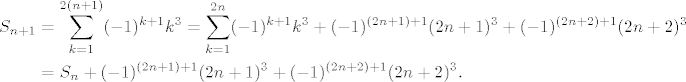
Dakle, nova suma ima dva elementa vise, pa ih "izvadimo" van i onda nam ostane "suma za prvih n elemenata plus ta dva viska". 
Dalje je lako: uvrstis pretpostavku indukcije i sredis; trebas dobiti
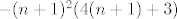 . . 
Jos ti ostane baza indukcije (za n=1), no to je trivijalno. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
oblak24
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (20:48:46)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:17 čet, 20. 8. 2009 Naslov: Postano: 14:17 čet, 20. 8. 2009 Naslov: |
    |
|
|
"Princip" radi na ovom zadatku; treba razumijeti sto je suma. :) Pazi ovdje:
[latex]\sum{k=a}^b x_k = x_a + x_{a+1} + \dots + x_b[/latex]
Dakle, oznaka [latex]\sum_{k=a}^b x_k[/latex] znaci "zbroji sve [latex]x_k[/latex] za koje je [i]k[/i] izmedju [i]a[/i] i [i]b[/i] (ukljucivo)". 8) Te vrijednosti ([i]a[/i], [i]a[/i]+1,... [i]b[/i]-1, [i]b[/i]) se, naravno, jednostavno uvrste u [i]k[/i]. 8)
Tvoja suma
[latex]S_n := \sum_{k=1}^{2n} (-1)^{k+1} k^3[/latex]
izgleda ovako (kad se raspise):
[latex]S_n = \sum_{k=1}^{2n} (-1)^{k+1} k^3 = (-1)^{1+1} 1^3 + (-1)^{2+1} 2^3 + \dots + (-1)^{2n+1} (2n)^3[/latex]
Za konkretne vrijednosti [i]n[/i]:
n = 1 :arrow: [latex]$\begin{align*}S_1 &= \sum_{k=1}^{2\cdot 1} (-1)^{k+1} k^3 = \sum_{k=1}^2 (-1)^{k+1} k^3 \\ &= (-1)^{1+1} 1^3 + (-1)^{2+1} 2^3\end{align*}$[/latex]
n = 2 :arrow: [latex]$\begin{align*}S_1 &= \sum_{k=1}^{2\cdot 2} (-1)^{k+1} k^3 = \sum_{k=1}^4 (-1)^{k+1} k^3 \\ &= (-1)^{1+1} 1^3 + (-1)^{2+1} 2^3 + (-1)^{3+1} 3^3 + (-1)^{4+1} 4^3\end{align*}$[/latex]
n = 3 :arrow: [latex]$\begin{align*}S_1 &= \sum_{k=1}^{2\cdot 3} (-1)^{k+1} k^3 = \sum_{k=1}^4 (-1)^{k+1} k^3 \\ &= (-1)^{1+1} 1^3 + (-1)^{2+1} 2^3 + (-1)^{3+1} 3^3 + (-1)^{4+1} 4^3 + (-1)^{5+1} 5^3 + (-1)^{6+1} 6^3\end{align*}$[/latex]
...
Jasnije? :D
"Princip" radi na ovom zadatku; treba razumijeti sto je suma.  Pazi ovdje: Pazi ovdje:
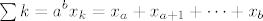
Dakle, oznaka 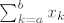 znaci "zbroji sve znaci "zbroji sve 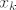 za koje je k izmedju a i b (ukljucivo)". za koje je k izmedju a i b (ukljucivo)".  Te vrijednosti (a, a+1,... b-1, b) se, naravno, jednostavno uvrste u k. Te vrijednosti (a, a+1,... b-1, b) se, naravno, jednostavno uvrste u k. 
Tvoja suma
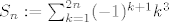
izgleda ovako (kad se raspise):
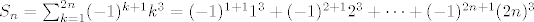
Za konkretne vrijednosti n:
n = 1  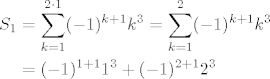
n = 2  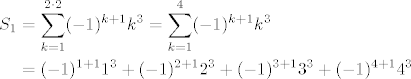
n = 3  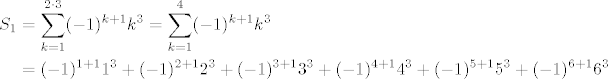
...
Jasnije? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|








