|
Da, pretpostavljam da bismo to mogli zvati mnogostrukost algebri, no nisam siguran koji je točan hrvatski naziv.
Napomena: Post koji slijedi je ispao nešto duži nego što sam planirao. Jedan od razloga zašto sam ga napisao je da i sebi posložim neke stvari u glavi. Kako ne bih uplašio ljude koji slučajno nabasaju na ovo, reći ću samo da ovo što slijedi [i]nije[/i] dio gradiva kolegija Algebarskih struktura. Ako ipak netko želi pročitati i shvatiti napisano, za neke pojmove vjerojatno će morati pogledati [url=http://vedgar.googlepages.com/Logika_skipta.pdf]skriptu[/url] prof. Vukovića iz Matematičke logike. I još, kad kažem [i]klasa[/i], mislim na pravu klasu, ne nužno skup.
@Grga: Ono što te možda zbunjuje je sama riječ [i]algebra[/i] koja u ovom kontekstu zapravo znači [i]algebarska struktura[/i]. Dakle, bilo kakav skup (nosač) zajedno s proizvoljnim skupom operacija. Formalna definicija:
[b]D1. (Signatura)[/b] [i]Signatura[/i] je uređen par [latex]\mathcal{F}=(F,\rho)[/latex], pri čemu je [latex]F[/latex] neprazan skup [i]funkcijskih simbola[/i], a [latex]\rho\colon F\to\mathbb{N}[/latex] funkcija koja svakom funkcijskom simbolu [latex]f[/latex] pridružuje [i]mjesnost[/i]---broj argumenata na koje se [latex]f[/latex] može primijeniti. Nul-mjesne funkcijske simbole zovemo [i]konstantski simboli[/i].
[b]D2. (Algebra)[/b] Neka je [latex]\mathcal{F}[/latex] signatura. [i]Algebra[/i] signature [latex]\mathcal{F}[/latex] je uređen par [latex]\mathcal{A}=(A,I)[/latex], pri čemu je [latex]A[/latex] neprazan skup (nosač), a [latex]I[/latex] je funkcija (interpretacija) koja svakom funkcijskom simbolu [latex]f[/latex] mjesnosti [latex]n[/latex] pridružuje funkciju (operaciju) [latex]f_\mathcal{A}[/latex] s [latex]A^n[/latex] u [latex]A[/latex].
To je znači precizna definicija onog što zovemo algebarskom strukturom. Grana matematike koja proučava općenite algebarske strukture se zove univerzalna algebra.
Sad bismo mogli definirati homomorfizme i izomorfizme algebri s istom signaturom, a onda i homomorfne slike: algebra [latex]\mathcal{B}[/latex] je homomorfna slika algebre [latex]\mathcal{A}[/latex] ako postoji [i]surjektivni[/i] homomorfizam s [latex]\mathcal{A}[/latex] na [latex]\mathcal{B}[/latex]. Ako imamo klasu [latex]\mathsf{C}[/latex] algebri neke signature, s [latex]\mathbf{H}\mathsf{C}[/latex] označavamo klasu svih homomorfnih slika algebri iz [latex]\mathsf{C}[/latex].
Nadalje, mogli bismo definirati podalgebru neke algebre (tu bi bila bitna zatvorenost na sve operacije). Sa [latex]\mathbf{S}\mathsf{C}[/latex] bismo označili klasu izomorfnih kopija podalgebri svih algebri iz [latex]\mathsf{C}[/latex].
I na kraju, definirali bismo produkt familije algebri [latex](\mathcal{A}_i)_{i\in I}[/latex] kao algebru čiji je nosač Kartezijev produkt skupova [latex]\mathcal{A}_i[/latex], a operacije su definirane po komponentama. S [latex]\mathbf{P}\mathsf{C}[/latex] bismo označili klasu izomorfnih kopija produkata algebri iz [latex]\mathsf{C}[/latex].
Kad imamo sve to, možemo definirati mnogostrukost algebri:
[b]D3. (Mnogostrukost)[/b] Klasa algebri iste signature je [i]mnogostrukost[/i] ako je zatvorena na podalgebre, homomorfne slike i produkte. Za klasu [latex]\mathsf{C}[/latex] s [latex]\mathbb{V}\mathsf{C}[/latex] označimo najmanju mnogostrukost koja sadrži [latex]\mathsf{C}[/latex], tj. mnogostrukost generiranu klasom [latex]\mathsf{C}[/latex].
Jedan od poznatih rezultata iz ovog područja je [latex]\mathbb{V}\mathsf{C}=\mathbf{HSP}\mathsf{C}[/latex]. Dakle, mnogostrukost generiranu klasom [latex]\mathsf{C}[/latex] dobijemo tako da uzmemo zatvorenje klase [latex]\mathsf{C}[/latex] na produkte, zatim uzmemo zatvorenje dobivene klase na podalgebre te na kraju zatvorenje svega na homomorfne slike.
E sad, daljnja priča bi bila o nečem što se zove algebarska teorija modela. Naime, ako krenemo od signature [latex]\mathcal{F}[/latex] i skupa varijabli [latex]X[/latex], mogli bismo induktivno definirati pojam [i]terma[/i] kao i u kolegiju Matematička logika. Dalje bismo definirali [i]jednadžbu[/i] kao izraz [latex]s\approx t[/latex], pri čemu su [latex]s[/latex] i [latex]t[/latex] termi.
Kad imamo sintaksu (terme i jednadžbe), algebarsku semantiku dobijemo tako da [i]valuiramo[/i] terme u algebrama odgovarajuće signature. Dakle, induktivno bismo definirali [i]valuaciju[/i] kao funkciju [latex]\theta[/latex] sa skupa svih terma u nosač algebre [latex]\mathcal{A}[/latex]. Tad bismo rekli da je jednadžba [latex]s\approx t[/latex] [i]istinita[/i], ili da [i]vrijedi[/i] u [latex]\mathcal{A}[/latex] ako za sve valuacije [latex]\theta[/latex] vrijedi [latex]\theta(s)=\theta(t)[/latex]. Algebru [latex]\mathcal{A}[/latex] zovemo [i]modelom[/i] za [latex]s\approx t[/latex] ako je [latex]s\approx t[/latex] istinita u [latex]\mathcal{A}[/latex].
[b]D4. (Definabilne klase)[/b] Kažemo da je klasa [latex]\mathsf{C}[/latex] algebri iste signature [i]definabilna jednadžbama[/i] ako postoji skup jednadžbi [latex]E[/latex] takav da [latex]\mathsf{C}[/latex] sadrži sve modele svih jednadžbi iz [latex]E[/latex], i samo njih.
Primjer definabilne klase je npr. klasa svih grupa, pri čemu grupu promatramo kao algebru signature [latex]\{\cdot,{}^{-1},\mathbf{e}\}[/latex] (prvo je dvomjesni, drugo jednomjesni funkcijski, a treće nul-mjesni, tj. konstantski simbol). Skup jednadžbi koji definira klasu svih grupa je [latex]\{x\cdot (y\cdot z)\approx (x\cdot y)\cdot z, x\cdot \mathbf{e}\approx x, x\cdot x^{-1}\approx \mathbf{e}\}[/latex].
I da zaključim, slijedi osnovni rezultat iz ovog područja, tzv. Birkhoffov teorem:
[b]T. (Birkhoff)[/b] Klasa algebri iste signature je definabilna jednadžbama ako i samo ako je mnogostrukost.
Da, pretpostavljam da bismo to mogli zvati mnogostrukost algebri, no nisam siguran koji je točan hrvatski naziv.
Napomena: Post koji slijedi je ispao nešto duži nego što sam planirao. Jedan od razloga zašto sam ga napisao je da i sebi posložim neke stvari u glavi. Kako ne bih uplašio ljude koji slučajno nabasaju na ovo, reći ću samo da ovo što slijedi nije dio gradiva kolegija Algebarskih struktura. Ako ipak netko želi pročitati i shvatiti napisano, za neke pojmove vjerojatno će morati pogledati skriptu prof. Vukovića iz Matematičke logike. I još, kad kažem klasa, mislim na pravu klasu, ne nužno skup.
@Grga: Ono što te možda zbunjuje je sama riječ algebra koja u ovom kontekstu zapravo znači algebarska struktura. Dakle, bilo kakav skup (nosač) zajedno s proizvoljnim skupom operacija. Formalna definicija:
D1. (Signatura) Signatura je uređen par 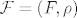 , pri čemu je , pri čemu je 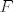 neprazan skup funkcijskih simbola, a neprazan skup funkcijskih simbola, a 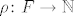 funkcija koja svakom funkcijskom simbolu funkcija koja svakom funkcijskom simbolu  pridružuje mjesnost—broj argumenata na koje se pridružuje mjesnost—broj argumenata na koje se  može primijeniti. Nul-mjesne funkcijske simbole zovemo konstantski simboli. može primijeniti. Nul-mjesne funkcijske simbole zovemo konstantski simboli.
D2. (Algebra) Neka je 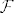 signatura. Algebra signature signatura. Algebra signature 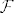 je uređen par je uređen par  , pri čemu je , pri čemu je  neprazan skup (nosač), a neprazan skup (nosač), a 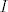 je funkcija (interpretacija) koja svakom funkcijskom simbolu je funkcija (interpretacija) koja svakom funkcijskom simbolu  mjesnosti mjesnosti  pridružuje funkciju (operaciju) pridružuje funkciju (operaciju) 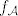 s s  u u  . .
To je znači precizna definicija onog što zovemo algebarskom strukturom. Grana matematike koja proučava općenite algebarske strukture se zove univerzalna algebra.
Sad bismo mogli definirati homomorfizme i izomorfizme algebri s istom signaturom, a onda i homomorfne slike: algebra 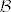 je homomorfna slika algebre je homomorfna slika algebre 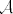 ako postoji surjektivni homomorfizam s ako postoji surjektivni homomorfizam s 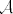 na na 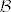 . Ako imamo klasu . Ako imamo klasu 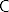 algebri neke signature, s algebri neke signature, s 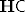 označavamo klasu svih homomorfnih slika algebri iz označavamo klasu svih homomorfnih slika algebri iz 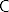 . .
Nadalje, mogli bismo definirati podalgebru neke algebre (tu bi bila bitna zatvorenost na sve operacije). Sa  bismo označili klasu izomorfnih kopija podalgebri svih algebri iz bismo označili klasu izomorfnih kopija podalgebri svih algebri iz 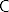 . .
I na kraju, definirali bismo produkt familije algebri  kao algebru čiji je nosač Kartezijev produkt skupova kao algebru čiji je nosač Kartezijev produkt skupova 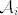 , a operacije su definirane po komponentama. S , a operacije su definirane po komponentama. S 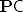 bismo označili klasu izomorfnih kopija produkata algebri iz bismo označili klasu izomorfnih kopija produkata algebri iz 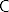 . .
Kad imamo sve to, možemo definirati mnogostrukost algebri:
D3. (Mnogostrukost) Klasa algebri iste signature je mnogostrukost ako je zatvorena na podalgebre, homomorfne slike i produkte. Za klasu 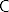 s s 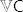 označimo najmanju mnogostrukost koja sadrži označimo najmanju mnogostrukost koja sadrži 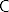 , tj. mnogostrukost generiranu klasom , tj. mnogostrukost generiranu klasom 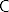 . .
Jedan od poznatih rezultata iz ovog područja je  . Dakle, mnogostrukost generiranu klasom . Dakle, mnogostrukost generiranu klasom 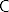 dobijemo tako da uzmemo zatvorenje klase dobijemo tako da uzmemo zatvorenje klase 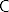 na produkte, zatim uzmemo zatvorenje dobivene klase na podalgebre te na kraju zatvorenje svega na homomorfne slike. na produkte, zatim uzmemo zatvorenje dobivene klase na podalgebre te na kraju zatvorenje svega na homomorfne slike.
E sad, daljnja priča bi bila o nečem što se zove algebarska teorija modela. Naime, ako krenemo od signature 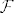 i skupa varijabli i skupa varijabli  , mogli bismo induktivno definirati pojam terma kao i u kolegiju Matematička logika. Dalje bismo definirali jednadžbu kao izraz , mogli bismo induktivno definirati pojam terma kao i u kolegiju Matematička logika. Dalje bismo definirali jednadžbu kao izraz 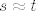 , pri čemu su , pri čemu su  i i  termi. termi.
Kad imamo sintaksu (terme i jednadžbe), algebarsku semantiku dobijemo tako da valuiramo terme u algebrama odgovarajuće signature. Dakle, induktivno bismo definirali valuaciju kao funkciju 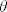 sa skupa svih terma u nosač algebre sa skupa svih terma u nosač algebre 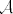 . Tad bismo rekli da je jednadžba . Tad bismo rekli da je jednadžba 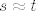 istinita, ili da vrijedi u istinita, ili da vrijedi u 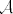 ako za sve valuacije ako za sve valuacije 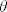 vrijedi vrijedi  . Algebru . Algebru 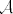 zovemo modelom za zovemo modelom za 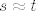 ako je ako je 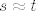 istinita u istinita u 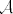 . .
D4. (Definabilne klase) Kažemo da je klasa 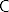 algebri iste signature definabilna jednadžbama ako postoji skup jednadžbi algebri iste signature definabilna jednadžbama ako postoji skup jednadžbi 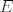 takav da takav da 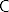 sadrži sve modele svih jednadžbi iz sadrži sve modele svih jednadžbi iz 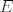 , i samo njih. , i samo njih.
Primjer definabilne klase je npr. klasa svih grupa, pri čemu grupu promatramo kao algebru signature 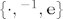 (prvo je dvomjesni, drugo jednomjesni funkcijski, a treće nul-mjesni, tj. konstantski simbol). Skup jednadžbi koji definira klasu svih grupa je (prvo je dvomjesni, drugo jednomjesni funkcijski, a treće nul-mjesni, tj. konstantski simbol). Skup jednadžbi koji definira klasu svih grupa je  . .
I da zaključim, slijedi osnovni rezultat iz ovog područja, tzv. Birkhoffov teorem:
T. (Birkhoff) Klasa algebri iste signature je definabilna jednadžbama ako i samo ako je mnogostrukost.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|







