|
Obećao sam ovdje napisati rješenje jednog zadatka, pa evo. :)
[b]ZADATAK.[/b]
Dan je linearno nezavisan skup [latex]\left\{x,\, y\right\}[/latex] u vektorskom prostoru dimenzije [latex]n \geq 2[/latex] nad poljem [latex]\mathbb{F}[/latex]. Odredite nužne i dovoljne uvjete na skalare [latex]\alpha,\, \beta,\, \gamma,\, \delta \in \mathbb{F}[/latex] tako da i skup [latex]\left\{\alpha x + \beta y,\, \gamma x + \delta y\right\}[/latex] bude linearno nezavisan.
[b]RJEŠENJE.[/b]
Neka je [latex]\alpha x + \beta y = v_1[/latex], [latex]\gamma x + \delta y = v_2[/latex]. Pretpostavimo da je skup [latex]\left\{v_1,\, v_2\right\}[/latex] također linearno nezavisan. To znači da vrijedi implikacija (gdje su, naravno, [latex]a,\, b \in \mathbb{F}[/latex]) [latex]av_1 + bv_2 = 0 \Longrightarrow a=b=0[/latex]. Dakle, jedino rješenje sustava (po [latex]a,\, b[/latex]):
[latex] \left\{ \begin{array}{ccc}
\alpha a + \gamma b & = & 0, \\
\beta a + \delta b & = & 0,
\end{array} \right. (*)[/latex]
je [latex]a=b=0[/latex].
Promotrimo dva slučaja.
1° Neka je [latex]\alpha \neq 0[/latex]. Tada prvu jednadžbu sustava možemo pomnožiti s [latex]\frac{-\beta}{\alpha}[/latex] i pribrojiti joj drugu, pa dobivamo:
[latex]\left(\delta - \frac{\beta \gamma}{\alpha}\right) b = 0[/latex].
Želimo da je nužno [latex]b=0[/latex], stoga mora biti [latex]\delta \neq \frac{\beta \gamma}{\alpha}[/latex], odnosno
[latex]\alpha \delta \neq \beta \gamma[/latex]. Jasno je da iz [latex]\alpha \neq 0[/latex] i [latex]b=0[/latex] odmah slijedi da je [latex]a=0[/latex].
2° Neka je [latex]\alpha=0[/latex]. U prvoj jednadžbi tada dobivamo da je [latex]\gamma b = 0[/latex], kako želimo da je nužno [latex]b=0[/latex] vidimo da mora biti [latex]\gamma \neq 0[/latex].
U drugoj jednadži nam sada ostaje [latex]\beta a = 0[/latex] iz čega vidimo da mora biti [latex]\beta \neq 0[/latex].
Kako je [latex]\alpha=0[/latex] i [latex]\beta \neq 0[/latex], [latex]\gamma \neq 0[/latex], vidimo da opet možemo pisati
[latex]\alpha \delta \neq \beta \gamma[/latex].
Ovime smo pokazali da je uvjet [latex]\alpha \delta \neq \beta \gamma[/latex] nužan, pokažimo da je on i dovoljan.
Neka je [latex]\alpha \delta \neq \beta \gamma[/latex]. Rješavamo sustav [latex](*)[/latex]. Promotrimo dva slučaja.
1° Neka je [latex]\alpha = 0[/latex]. Tada je [latex]\beta \gamma \neq 0[/latex].
Prva jednadžba postaje [latex]\gamma b = 0[/latex], no, kako je [latex]\gamma \neq 0[/latex], dobivamo [latex]b=0[/latex].
Uvrštavajući dobiveno u drugu jednadžbu i koristeći [latex]\beta \neq 0[/latex] dobivamo i [latex]a=0[/latex].
2° Neka je [latex]\alpha \neq 0[/latex]. Sada možemo prvu jednadžbu sustava pomnožiti s [latex]\frac{-\beta}{\alpha}[/latex] i pribojiti dobiveno drugoj.
Dobivamo da je [latex]\left(\delta - \frac{\beta \gamma}{\alpha}\right) b = 0 \Longleftrightarrow \left(\alpha \delta - \beta \gamma\right) b = 0 \Longrightarrow b=0[/latex].
Uvrštavajući dobiveno u prvu jednadžbu i koristeći [latex]\alpha \neq 0[/latex] dobivamo da je [latex]a=0[/latex].
Ovime smo pokazali da je nužan i dovoljan uvjet: [latex]\alpha \delta \neq \beta \gamma[/latex].
Obećao sam ovdje napisati rješenje jednog zadatka, pa evo. 
ZADATAK.
Dan je linearno nezavisan skup 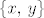 u vektorskom prostoru dimenzije u vektorskom prostoru dimenzije 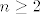 nad poljem nad poljem 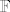 . Odredite nužne i dovoljne uvjete na skalare . Odredite nužne i dovoljne uvjete na skalare 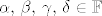 tako da i skup tako da i skup 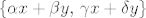 bude linearno nezavisan. bude linearno nezavisan.
RJEŠENJE.
Neka je 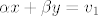 , , 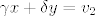 . Pretpostavimo da je skup . Pretpostavimo da je skup 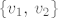 također linearno nezavisan. To znači da vrijedi implikacija (gdje su, naravno, također linearno nezavisan. To znači da vrijedi implikacija (gdje su, naravno, 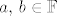 ) ) 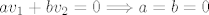 . Dakle, jedino rješenje sustava (po . Dakle, jedino rješenje sustava (po 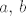 ): ):
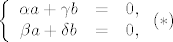
je 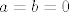 . .
Promotrimo dva slučaja.
1° Neka je 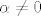 . Tada prvu jednadžbu sustava možemo pomnožiti s . Tada prvu jednadžbu sustava možemo pomnožiti s 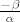 i pribrojiti joj drugu, pa dobivamo: i pribrojiti joj drugu, pa dobivamo:
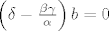 . .
Želimo da je nužno 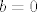 , stoga mora biti , stoga mora biti 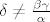 , odnosno , odnosno
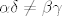 . Jasno je da iz . Jasno je da iz 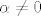 i i 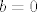 odmah slijedi da je odmah slijedi da je 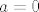 . .
2° Neka je  . U prvoj jednadžbi tada dobivamo da je . U prvoj jednadžbi tada dobivamo da je 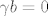 , kako želimo da je nužno , kako želimo da je nužno 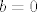 vidimo da mora biti vidimo da mora biti 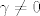 . .
U drugoj jednadži nam sada ostaje 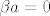 iz čega vidimo da mora biti iz čega vidimo da mora biti 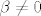 . .
Kako je  i i 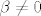 , , 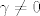 , vidimo da opet možemo pisati , vidimo da opet možemo pisati
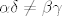 . .
Ovime smo pokazali da je uvjet 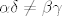 nužan, pokažimo da je on i dovoljan. nužan, pokažimo da je on i dovoljan.
Neka je 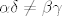 . Rješavamo sustav . Rješavamo sustav  . Promotrimo dva slučaja. . Promotrimo dva slučaja.
1° Neka je  . Tada je . Tada je 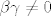 . .
Prva jednadžba postaje 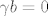 , no, kako je , no, kako je 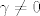 , dobivamo , dobivamo 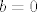 . .
Uvrštavajući dobiveno u drugu jednadžbu i koristeći 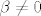 dobivamo i dobivamo i 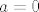 . .
2° Neka je 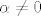 . Sada možemo prvu jednadžbu sustava pomnožiti s . Sada možemo prvu jednadžbu sustava pomnožiti s 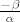 i pribojiti dobiveno drugoj. i pribojiti dobiveno drugoj.
Dobivamo da je 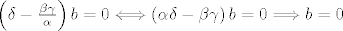 . .
Uvrštavajući dobiveno u prvu jednadžbu i koristeći 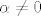 dobivamo da je dobivamo da je 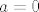 . .
Ovime smo pokazali da je nužan i dovoljan uvjet: 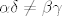 . .
|





