| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
val
Forumaš(ica)

Pridružen/a: 07. 10. 2008. (09:58:56)
Postovi: (8)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:01 pet, 16. 10. 2009 Naslov: Postano: 16:01 pet, 16. 10. 2009 Naslov: |
    |
|
|
sve ove medote baziraju se na jednostavnoj stvari, a to je rješavanje trokutastih sustava.
Npr neka je A poz definitna, onda ima faktorizaciju Choleski. To znači da se A može napisati kao [latex]A=R^t R[/latex] pri čemu je R gornjetrokutasta. (tada je Rt donje trokutasta)
Sad ako rješavamo Ax=b, to zapišemo kao
[latex]R^t R x =b[/latex]
najprije označimo Rx=y pa ustvari rješavamo
[latex]R^t y =b[/latex]
to je sustav sa donje trokutastom matricom, i rješava se supstitucijom unaprijed. to znači da odmah možemo izračunat y1 (=b1/r11) , s njim odemo u 2.jednadžbu koja kaže r21 y1+ r22 y2 =b2 pa dobijemo y2 i tako dalje.
Na taj način dobijemo y, i vratimo se u
Rx=y
ovo je opet trokutast sustav, samo sa gornjetrokutastom matricom, pa supstitucija ide unatrag (prvo dobijemo xn, pa x(n-1) itd. )
Kod SVD-a (koju ima svaka matrica) tm kaže da se A može zapisati kao
[latex]A = U D V^*[/latex] gdje su U i V unitarne, a D diagonalna sa sing vrijednostima na dijagonali. U i V matrice su unitarne, pa su njihovi inverzi jednostavno U* i V* ( jer je U U* =I ).
Kada s tim rješavamo sustav imao:
[latex]A x =b[/latex]
[latex]U D V^* x =b[/latex]
pa x dobijemo kao
[latex] x =V \cdot D^{-1} \cdot U^* \cdot b[/latex]
D^-1 nam je lako izračunat (to je dij matrica sa recipročnim vrijednostima od D na dijagonali).
Kod QR-a je sve slično, Q je ortogonalna, pa joj je inverz samo transponirana matrica, a onda trebamo trokutast sustav riješit (jer je R trokutasta), što sam već gore opisao.
sve ove medote baziraju se na jednostavnoj stvari, a to je rješavanje trokutastih sustava.
Npr neka je A poz definitna, onda ima faktorizaciju Choleski. To znači da se A može napisati kao 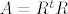 pri čemu je R gornjetrokutasta. (tada je Rt donje trokutasta) pri čemu je R gornjetrokutasta. (tada je Rt donje trokutasta)
Sad ako rješavamo Ax=b, to zapišemo kao
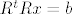
najprije označimo Rx=y pa ustvari rješavamo
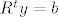
to je sustav sa donje trokutastom matricom, i rješava se supstitucijom unaprijed. to znači da odmah možemo izračunat y1 (=b1/r11) , s njim odemo u 2.jednadžbu koja kaže r21 y1+ r22 y2 =b2 pa dobijemo y2 i tako dalje.
Na taj način dobijemo y, i vratimo se u
Rx=y
ovo je opet trokutast sustav, samo sa gornjetrokutastom matricom, pa supstitucija ide unatrag (prvo dobijemo xn, pa x(n-1) itd. )
Kod SVD-a (koju ima svaka matrica) tm kaže da se A može zapisati kao
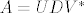 gdje su U i V unitarne, a D diagonalna sa sing vrijednostima na dijagonali. U i V matrice su unitarne, pa su njihovi inverzi jednostavno U* i V* ( jer je U U* =I ). gdje su U i V unitarne, a D diagonalna sa sing vrijednostima na dijagonali. U i V matrice su unitarne, pa su njihovi inverzi jednostavno U* i V* ( jer je U U* =I ).
Kada s tim rješavamo sustav imao:
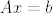
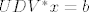
pa x dobijemo kao
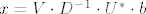
D^-1 nam je lako izračunat (to je dij matrica sa recipročnim vrijednostima od D na dijagonali).
Kod QR-a je sve slično, Q je ortogonalna, pa joj je inverz samo transponirana matrica, a onda trebamo trokutast sustav riješit (jer je R trokutasta), što sam već gore opisao.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
val
Forumaš(ica)

Pridružen/a: 07. 10. 2008. (09:58:56)
Postovi: (8)16
|
|
| [Vrh] |
|
annna
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (14:53:52)
Postovi: (CF)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 18:59 pet, 16. 10. 2009 Naslov: Postano: 18:59 pet, 16. 10. 2009 Naslov: |
    |
|
|
Cholesky i QR su faktorizacije; SVD je dekompozicija. Ne "davim" s time bezveze:
- faktorizacija znaci, jednostavno receno, da izracunas direktno (u konacno mnogo koraka). Kod QR i Choleskog, to se radi jednim prolazom kroz matricu; oboje dobro objasnjeno u knjizi koju je annna preporucila, a cini mi se da ima i na Wikipediji. Pogledas formule i provedes. QR je tu brzi jer, ako koristis Householderove reflektore (na Wikipediji imas tocne formule), imas samo n-1 koraka (za matricu reda nxn; za svaki stupac osim zadnjeg po jedan korak).
- dekompozicija znaci da ne mozes direktno izracunati, nego ti treba neki iterativni postupak. Teoretski, stvar konvergira rjesenju, no ne dodjes do tocnog rjesenja u konacno mnogo koraka. Medju najpoznatijim algoritmima su Jacobijevi, no obicno se koriste kombinacije. Npr. prvo napravis QR ili bidijagonalizaciju, pa onda napadnes samo ne-unitarni faktor.
Zbog toga, SVD - osim za matricu 2x2 - vjerojatno neces racunati na ruke, nego preko Mathematice, MATLABa, funkcija iz LAPACKa,... nekako strojno.
Mali ispravak Luuke: sve tri metode se baziraju na laganom racunanju inzverza, a ne na trokutastosti.
Cholesky - da, dva trokutna sustava,
QR - trokut i unitarac,
SVD - unitarci i dijagonala.
Vidljivo iz ostatka Luukinog posta, ali ipak da i taj dio pise korektno. ;)
Cholesky i QR su faktorizacije; SVD je dekompozicija. Ne "davim" s time bezveze:
- faktorizacija znaci, jednostavno receno, da izracunas direktno (u konacno mnogo koraka). Kod QR i Choleskog, to se radi jednim prolazom kroz matricu; oboje dobro objasnjeno u knjizi koju je annna preporucila, a cini mi se da ima i na Wikipediji. Pogledas formule i provedes. QR je tu brzi jer, ako koristis Householderove reflektore (na Wikipediji imas tocne formule), imas samo n-1 koraka (za matricu reda nxn; za svaki stupac osim zadnjeg po jedan korak).
- dekompozicija znaci da ne mozes direktno izracunati, nego ti treba neki iterativni postupak. Teoretski, stvar konvergira rjesenju, no ne dodjes do tocnog rjesenja u konacno mnogo koraka. Medju najpoznatijim algoritmima su Jacobijevi, no obicno se koriste kombinacije. Npr. prvo napravis QR ili bidijagonalizaciju, pa onda napadnes samo ne-unitarni faktor.
Zbog toga, SVD - osim za matricu 2x2 - vjerojatno neces racunati na ruke, nego preko Mathematice, MATLABa, funkcija iz LAPACKa,... nekako strojno.
Mali ispravak Luuke: sve tri metode se baziraju na laganom racunanju inzverza, a ne na trokutastosti.
Cholesky - da, dva trokutna sustava,
QR - trokut i unitarac,
SVD - unitarci i dijagonala.
Vidljivo iz ostatka Luukinog posta, ali ipak da i taj dio pise korektno. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:39 pet, 16. 10. 2009 Naslov: Postano: 19:39 pet, 16. 10. 2009 Naslov: |
    |
|
|
[quote="vsego"]
Mali ispravak Luuke: sve tri metode se baziraju na laganom racunanju inzverza, a ne na trokutastosti.
[/quote]
Joj dobro, bio je to početak posta, prije nego sam sve krenuo objašnjavat pa sam zaboravio promijenit. :D
Inače, postoji još jedna korisna faktorizacija, to je SPEKTRALNA, ali nju nemaju sve matrice (recimo simetrične sigurno imaju, kao poseban slučaj normalnih). Taj teorem kaže da se kvadratna matrica (ponavljam, ne svaka) može zapisati u obliku
[latex]A=U L U^*[/latex]
gdje je L dijagonalna sa svojstvenim vrijednostima od A na dijagonali, a stupci od U su pripadni svojstveni vektori.
(to je posljedica Schurove dekompozicije (koju ima svaka kvadratna matrica), koja bi isto mogla bit korisna - pojavljuje se trokutasta, a ne dijagonalna).
Malo istraži pa vidi šta sve ima :D
| vsego (napisa): |
Mali ispravak Luuke: sve tri metode se baziraju na laganom racunanju inzverza, a ne na trokutastosti.
|
Joj dobro, bio je to početak posta, prije nego sam sve krenuo objašnjavat pa sam zaboravio promijenit. 
Inače, postoji još jedna korisna faktorizacija, to je SPEKTRALNA, ali nju nemaju sve matrice (recimo simetrične sigurno imaju, kao poseban slučaj normalnih). Taj teorem kaže da se kvadratna matrica (ponavljam, ne svaka) može zapisati u obliku
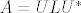
gdje je L dijagonalna sa svojstvenim vrijednostima od A na dijagonali, a stupci od U su pripadni svojstveni vektori.
(to je posljedica Schurove dekompozicije (koju ima svaka kvadratna matrica), koja bi isto mogla bit korisna - pojavljuje se trokutasta, a ne dijagonalna).
Malo istraži pa vidi šta sve ima 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
val
Forumaš(ica)

Pridružen/a: 07. 10. 2008. (09:58:56)
Postovi: (8)16
|
 Postano: 23:20 pet, 16. 10. 2009 Naslov: pomoc Postano: 23:20 pet, 16. 10. 2009 Naslov: pomoc |
    |
|
|
Nasla sam SVD algoritam ali mi nije jasan njegov rad.
Na koji nacin on pronalazi matrice U, W i V.
Da li bi mi to netko bio voljan objasniti
#include <math.h>
#include "nrutil.h"
void svdcmp(float **a, int m, int n, float w[], float **v)
{
float pythag(float a, float b);
int flag,i,its,j,jj,k,l,nm;
float anorm,c,f,g,h,s,scale,x,y,z,*rv1;
rv1=vector(1,n);
g=scale=anorm=0.0; \\Householderova promjena oblika u bidiagonalnu formu.
for (i=1;i<=n;i++) {
l=i+1;
rv1[i]=scale*g;
g=s=scale=0.0;
if (i <= m) {
for (k=i;k<=m;k++) scale += fabs(a[k][i]);
if (scale) {
for (k=i;k<=m;k++) {
a[k][i] /= scale;
s += a[k][i]*a[k][i];
}
f=a[i][i];
g = -SIGN(sqrt(s),f);
h=f*g-s;
a[i][i]=f-g;
for (j=l;j<=n;j++) {
for (s=0.0,k=i;k<=m;k++) s += a[k][i]*a[k][j];
f=s/h;
for (k=i;k<=m;k++) a[k][j] += f*a[k][i];
}
for (k=i;k<=m;k++) a[k][i] *= scale;
}
}
w[i]=scale *g;
g=s=scale=0.0;
if(i<=m&&i!=n){
for (k=l;k<=n;k++) scale += fabs(a[i][k]);
if (scale) {
for (k=l;k<=n;k++) {
a[i][k] /= scale;
s += a[i][k]*a[i][k];
}
f=a[i][l];
g = -SIGN(sqrt(s),f);
h=f*g-s;
a[i][l]=f-g;
for (k=l;k<=n;k++) rv1[k]=a[i][k]/h;
for (j=l;j<=m;j++) {
for (s=0.0,k=l;k<=n;k++) s += a[j][k]*a[i][k];
for (k=l;k<=n;k++) a[j][k] += s*rv1[k];
}
for (k=l;k<=n;k++) a[i][k] *= scale;
}
}
anorm=FMAX(anorm,(fabs(w[i])+fabs(rv1[i])));
}
for (i=n;i>=1;i--) {
if(i<n){
if (g) {
for (j=l;j<=n;j++) \\dvostruko mnozenje radi donjeg limita
v[j][i]=(a[i][j]/a[i][l])/g;
for (j=l;j<=n;j++) {
for (s=0.0,k=l;k<=n;k++) s += a[i][k]*v[k][j];
for (k=l;k<=n;k++) v[k][j] += s*v[k][i];
}
}
for (j=l;j<=n;j++) v[i][j]=v[j][i]=0.0;
}
v[i][i]=1.0;
g=rv1[i];
l=i;
}
for (i=IMIN(m,n);i>=1;i--) {
l=i+1;
g=w[i];
for (j=l;j<=n;j++) a[i][j]=0.0;
if (g) {
g=1.0/g;
for (j=l;j<=n;j++) {
for (s=0.0,k=l;k<=m;k++) s += a[k][i]*a[k][j];
f=(s/a[i][i])*g;
for (k=i;k<=m;k++) a[k][j] += f*a[k][i];
}
for (j=i;j<=m;j++) a[j][i] *= g;
} else for (j=i;j<=m;j++) a[j][i]=0.0;
++a[i][i];
}
for (k=n;k>=1;k--) {
for (its=1;its<=30;its++) {
flag=1;
for (l=k;l>=1;l--) {
nm=l-1;
if ((float)(fabs(rv1[l])+anorm) == anorm) {
flag=0;
break;
}
if ((float)(fabs(w[nm])+anorm) == anorm) break;
}
if (flag) {
c=0.0;
s=1.0;
for (i=l;i<=k;i++) {
f=s*rv1[i];
rv1[i]=c*rv1[i];
if ((float)(fabs(f)+anorm) == anorm) break;
g=w[i];
h=pythag(f,g);
w[i]=h;
h=1.0/h;
c=g*h;
s = -f*h;
for (j=1;j<=m;j++) {
y=a[j][nm];
z=a[j][i];
a[j][nm]=y*c+z*s;
a[j][i]=z*c-y*s;
}
}
}
z=w[k];
if (l == k) {
if (z < 0.0) {
w[k] = -z;
for (j=1;j<=n;j++) v[j][k] = -v[j][k];
}
break;
}
if (its == 30) nrerror("no convergence in 30 svdcmp iterations");
x=w[l];
nm=k-1;
y=w[nm];
g=rv1[nm];
h=rv1[k];
f=((y-z)*(y+z)+(g-h)*(g+h))/(2.0*h*y);
g=pythag(f,1.0);
f=((x-z)*(x+z)+h*((y/(f+SIGN(g,f)))-h))/x;
c=s=1.0; Next QR transformation:
for (j=l;j<=nm;j++) {
i=j+1;
g=rv1[i];
y=w[i];
h=s*g;
g=c*g;
z=pythag(f,h);
rv1[j]=z;
c=f/z;
s=h/z;
f=x*c+g*s;
g = g*c-x*s;
h=y*s;
y*=c;
for (jj=1;jj<=n;jj++) {
x=v[jj][j];
z=v[jj][i];
v[jj][j]=x*c+z*s;
v[jj][i]=z*c-x*s;
}
z=pythag(f,h);
w[j]=z;
if (z) {
z=1.0/z;
c=f*z;
s=h*z;
}
f=c*g+s*y;
x=c*y-s*g;
for (jj=1;jj<=m;jj++) {
y=a[jj][j];
z=a[jj][i];
a[jj][j]=y*c+z*s;
a[jj][i]=z*c-y*s;
}
}
rv1[l]=0.0;
rv1[k]=f;
w[k]=x;
}
}
free_vector(rv1,1,n);
}
Nasla sam SVD algoritam ali mi nije jasan njegov rad.
Na koji nacin on pronalazi matrice U, W i V.
Da li bi mi to netko bio voljan objasniti
#include <math.h>
#include "nrutil.h"
void svdcmp(float **a, int m, int n, float w[], float **v)
{
float pythag(float a, float b);
int flag,i,its,j,jj,k,l,nm;
float anorm,c,f,g,h,s,scale,x,y,z,*rv1;
rv1=vector(1,n);
g=scale=anorm=0.0; \\Householderova promjena oblika u bidiagonalnu formu.
for (i=1;i⇐n;i++) {
l=i+1;
rv1[i]=scale*g;
g=s=scale=0.0;
if (i ⇐ m) {
for (k=i;k⇐m;k++) scale += fabs(a[k][i]);
if (scale) {
for (k=i;k⇐m;k++) {
a[k][i] /= scale;
s += a[k][i]*a[k][i];
}
f=a[i][i];
g = -SIGN(sqrt(s),f);
h=f*g-s;
a[i][i]=f-g;
for (j=l;j⇐n;j++) {
for (s=0.0,k=i;k⇐m;k++) s += a[k][i]*a[k][j];
f=s/h;
for (k=i;k⇐m;k++) a[k][j] += f*a[k][i];
}
for (k=i;k⇐m;k++) a[k][i] *= scale;
}
}
w[i]=scale *g;
g=s=scale=0.0;
if(i⇐m&&i!=n){
for (k=l;k⇐n;k++) scale += fabs(a[i][k]);
if (scale) {
for (k=l;k⇐n;k++) {
a[i][k] /= scale;
s += a[i][k]*a[i][k];
}
f=a[i][l];
g = -SIGN(sqrt(s),f);
h=f*g-s;
a[i][l]=f-g;
for (k=l;k⇐n;k++) rv1[k]=a[i][k]/h;
for (j=l;j⇐m;j++) {
for (s=0.0,k=l;k⇐n;k++) s += a[j][k]*a[i][k];
for (k=l;k⇐n;k++) a[j][k] += s*rv1[k];
}
for (k=l;k⇐n;k++) a[i][k] *= scale;
}
}
anorm=FMAX(anorm,(fabs(w[i])+fabs(rv1[i])));
}
for (i=n;i>=1;i–) {
if(i<n){
if (g) {
for (j=l;j⇐n;j++) \\dvostruko mnozenje radi donjeg limita
v[j][i]=(a[i][j]/a[i][l])/g;
for (j=l;j⇐n;j++) {
for (s=0.0,k=l;k⇐n;k++) s += a[i][k]*v[k][j];
for (k=l;k⇐n;k++) v[k][j] += s*v[k][i];
}
}
for (j=l;j⇐n;j++) v[i][j]=v[j][i]=0.0;
}
v[i][i]=1.0;
g=rv1[i];
l=i;
}
for (i=IMIN(m,n);i>=1;i–) {
l=i+1;
g=w[i];
for (j=l;j⇐n;j++) a[i][j]=0.0;
if (g) {
g=1.0/g;
for (j=l;j⇐n;j++) {
for (s=0.0,k=l;k⇐m;k++) s += a[k][i]*a[k][j];
f=(s/a[i][i])*g;
for (k=i;k⇐m;k++) a[k][j] += f*a[k][i];
}
for (j=i;j⇐m;j++) a[j][i] *= g;
} else for (j=i;j⇐m;j++) a[j][i]=0.0;
++a[i][i];
}
for (k=n;k>=1;k–) {
for (its=1;its⇐30;its++) {
flag=1;
for (l=k;l>=1;l–) {
nm=l-1;
if ((float)(fabs(rv1[l])+anorm) == anorm) {
flag=0;
break;
}
if ((float)(fabs(w[nm])+anorm) == anorm) break;
}
if (flag) {
c=0.0;
s=1.0;
for (i=l;i⇐k;i++) {
f=s*rv1[i];
rv1[i]=c*rv1[i];
if ((float)(fabs(f)+anorm) == anorm) break;
g=w[i];
h=pythag(f,g);
w[i]=h;
h=1.0/h;
c=g*h;
s = -f*h;
for (j=1;j⇐m;j++) {
y=a[j][nm];
z=a[j][i];
a[j][nm]=y*c+z*s;
a[j][i]=z*c-y*s;
}
}
}
z=w[k];
if (l == k) {
if (z < 0.0) {
w[k] = -z;
for (j=1;j⇐n;j++) v[j][k] = -v[j][k];
}
break;
}
if (its == 30) nrerror("no convergence in 30 svdcmp iterations");
x=w[l];
nm=k-1;
y=w[nm];
g=rv1[nm];
h=rv1[k];
f=((y-z)*(y+z)+(g-h)*(g+h))/(2.0*h*y);
g=pythag(f,1.0);
f=((x-z)*(x+z)+h*((y/(f+SIGN(g,f)))-h))/x;
c=s=1.0; Next QR transformation:
for (j=l;j⇐nm;j++) {
i=j+1;
g=rv1[i];
y=w[i];
h=s*g;
g=c*g;
z=pythag(f,h);
rv1[j]=z;
c=f/z;
s=h/z;
f=x*c+g*s;
g = g*c-x*s;
h=y*s;
y*=c;
for (jj=1;jj⇐n;jj++) {
x=v[jj][j];
z=v[jj][i];
v[jj][j]=x*c+z*s;
v[jj][i]=z*c-x*s;
}
z=pythag(f,h);
w[j]=z;
if (z) {
z=1.0/z;
c=f*z;
s=h*z;
}
f=c*g+s*y;
x=c*y-s*g;
for (jj=1;jj⇐m;jj++) {
y=a[jj][j];
z=a[jj][i];
a[jj][j]=y*c+z*s;
a[jj][i]=z*c-y*s;
}
}
rv1[l]=0.0;
rv1[k]=f;
w[k]=x;
}
}
free_vector(rv1,1,n);
}
|
|
| [Vrh] |
|
|








