|
[quote="Tygy"]
1. dobar dio prve zadaće je ponavljanje linearne algebre, pa me zanima hoće li to ući u kolokvij? Jer, po proslogodisnjim kolokvijima, teorijska pitanja su iz linearne algebre (neka)?
2. nije da nisam uspjela naći biortogonalnu (dualnu ) bazu, al to na vježbama nismo radili...(90% sam sigurna u to :D ) pa jel se takve stvari mogu očekivati na kolokviju
3. koliko goD glupo zvučalo, jel mi može netko reći
dim L(L(C^2,C^3),L(C^4)) =? nisam sigurna... :roll:
4. Kako se traži A^-1 (inverz) pomoću minimlnog polinoma?
5. ne volim množit matrice!!! kako to izbjeć? (dok sam na kolokviju) :lol:[/quote]
1. pa dobar dio gradiva je ponavljanje linearne, tako da...
2. prošle godine je kolokvij bio preslika zadaća. Moguće da će to biti i ove, ali za svaki slučaj prođi i traženje dualne baze, nije teško :D
3. 6*16=96 valjda
4. slično ko preko karakterističnog :D
Imaš da matrica A poništava minimalni polinom, pa je
[latex]\alpha_0 I + \alpha_1 A + ... + \alpha_k A^k = 0[/latex]
(k je stupanj minimalnog polinoma, alfe su koeficijenti). Sad prebaciš ovaj dio di je identiteta na drugu stranu, podijeliš sa alfa0 (razl od nule ako je A regularna, razmisli zašto), pa onda pomnožiš sa A^-1 i dobiješ što se tražilo, tj:
[latex]A^{-1}= - \frac{\alpha_1}{\alpha_0} I - ... - \frac{\alpha_k}{\alpha_0} A^{k-1}[/latex]
5. teško da ćeš izbjeć ako će te to tražit :D
| Tygy (napisa): |
1. dobar dio prve zadaće je ponavljanje linearne algebre, pa me zanima hoće li to ući u kolokvij? Jer, po proslogodisnjim kolokvijima, teorijska pitanja su iz linearne algebre (neka)?
2. nije da nisam uspjela naći biortogonalnu (dualnu ) bazu, al to na vježbama nismo radili...(90% sam sigurna u to  ) pa jel se takve stvari mogu očekivati na kolokviju
3. koliko goD glupo zvučalo, jel mi može netko reći
dim L(L(C^2,C^3),L(C^4)) =? nisam sigurna... 
4. Kako se traži A^-1 (inverz) pomoću minimlnog polinoma?
5. ne volim množit matrice!!! kako to izbjeć? (dok sam na kolokviju)  |
1. pa dobar dio gradiva je ponavljanje linearne, tako da...
2. prošle godine je kolokvij bio preslika zadaća. Moguće da će to biti i ove, ali za svaki slučaj prođi i traženje dualne baze, nije teško
3. 6*16=96 valjda
4. slično ko preko karakterističnog
Imaš da matrica A poništava minimalni polinom, pa je
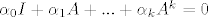
(k je stupanj minimalnog polinoma, alfe su koeficijenti). Sad prebaciš ovaj dio di je identiteta na drugu stranu, podijeliš sa alfa0 (razl od nule ako je A regularna, razmisli zašto), pa onda pomnožiš sa A^-1 i dobiješ što se tražilo, tj:
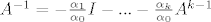
5. teško da ćeš izbjeć ako će te to tražit
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
