|
Danas smo na demonstraturama rješavali i ovakav zadatak:
Skup B=[latex]\{b_{1}, b_{2}, \ldots b_{n}\}[/latex] je sustav izvodnica za [latex]\mathbb{R}^{n}[/latex]. Dokaži da je on sustav izvodnica i za [latex]\mathbb{C}^{n}[/latex]
Nakon što smo ga prvo riješili ispravno, rekao sam i dugo objašnjavao da je zapravo trebalo promatrati komponente vektora. To nije bilo dobro. Zato sad dajem ispravno rješenje:
[latex]z \in \mathbb{C}^{n}, \beta_{j} \in \mathbb{C}, 1 \leq j \leq n[/latex]
pitanje je, zapravo, mogu li pronaci takve [latex]\beta_{j}[/latex] da vrijedi [latex]\sum_{j=1}^{n}\beta_{j}b_{j}=z[/latex]
[latex]z=x+iy[/latex], [latex]x,y \in \mathbb{R}^{n}[/latex]
[latex]\beta_{j}=a_{j}+c_{j}i[/latex],
[latex]a_{j}, c_{j} \in \mathbb{R}[/latex], [latex] \forall j[/latex]
sada jednadzba izgleda ovako:
[latex]\sum_{j=1}^{n}a_{j}b_{j} + \sum_{j=1}^{n}c_{j}b_{j}i=x+iy[/latex]
Kad izjednacimo realni dio lijeve i desne strane,
[latex]\sum_{j=1}^{n}a_{j}b_{j}=x[/latex]
Kako je B baza za [latex]\mathbb{R}^{n}[/latex], takve (realne) koeficijente [latex]a_{j}[/latex] mozemo pronaci.
Zatim izjednacimo imaginarne dijelove i na isti nacin zakljucimo da mozemo pronaci sve [latex]c_{j}[/latex],
a to znaci da mozemo pronaci sve [latex]a_{j}+c_{j}i=\beta_{j}[/latex]
takve da vrijedi [latex]\sum_{j=1}^{n}\beta_{j}b_{j}=z[/latex]
I zato je B zaista sustav izvodnica i za [latex]\mathbb{C}^{n}[/latex]
Zao mi je sto sam vas danas zbunio
Slicno se dokaze i za linearnu nezavisnost (originalni zadatak trazio je dokaz i jednog i drugog)
Danas smo na demonstraturama rješavali i ovakav zadatak:
Skup B=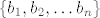 je sustav izvodnica za je sustav izvodnica za 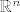 . Dokaži da je on sustav izvodnica i za . Dokaži da je on sustav izvodnica i za 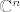
Nakon što smo ga prvo riješili ispravno, rekao sam i dugo objašnjavao da je zapravo trebalo promatrati komponente vektora. To nije bilo dobro. Zato sad dajem ispravno rješenje:
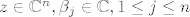
pitanje je, zapravo, mogu li pronaci takve 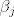 da vrijedi da vrijedi 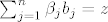
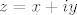 , , 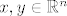
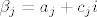 , ,
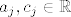 , , 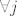
sada jednadzba izgleda ovako:
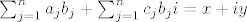
Kad izjednacimo realni dio lijeve i desne strane,
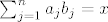
Kako je B baza za 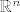 , takve (realne) koeficijente , takve (realne) koeficijente 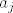 mozemo pronaci. mozemo pronaci.
Zatim izjednacimo imaginarne dijelove i na isti nacin zakljucimo da mozemo pronaci sve 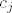 , ,
a to znaci da mozemo pronaci sve 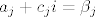
takve da vrijedi 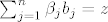
I zato je B zaista sustav izvodnica i za 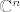
Zao mi je sto sam vas danas zbunio
Slicno se dokaze i za linearnu nezavisnost (originalni zadatak trazio je dokaz i jednog i drugog)
|




