|
@niveus: Ima tu jedan stari trik: naprosto pitaš asistenta :P. (A i, kad se traži inverzna funkcija, obično piše nešto u stilu "Odredi [latex]f^{-1}(x)[/latex].", a kad se traži praslika, zna pisati nešto u stilu "Odredi [latex]f^{-1}(A)[/latex].", gdje je [latex]A[/latex] neki skup. Ali ja bih se ipak držao prokušanog trika s asistentom :D.)
@kykica: U načelu, izgled prirodne domene uvijek je oblika [latex]U_1\cap U_2\cap \cdots \cap U_n[/latex], gdje je [latex]U_i[/latex] "prihvatljiva" domena za i-ti uvjet. Jesam malo neprecizan, ali mislim da ćeš shvatiti :). Na primjer, funkcija [latex]\frac{1}{x}+\frac{1}{x-1}[/latex] ima prvi uvjet [latex]x\neq 0[/latex], pa je [latex]U_1=\mathbb{R}\setminus\{0\}[/latex], a drugi uvjet [latex]x\neq 1[/latex], pa je [latex]U_2=\mathbb{R}\setminus\{1\}[/latex]. Sada je prirodna domena [latex](\mathbb{R}\setminus\{0\})\cap(\mathbb{R}\setminus\{1\})=\mathbb{R}\setminus\{0,1\}[/latex].
No, ono što tebe vjerojatno zbunjuje je da neki od tih skupova [latex]U_i[/latex] mogu biti unije same po sebi. Na primjer, ako tražiš prirodnu domenu funkcije [latex]\log (x^2+x)[/latex], onda je ona [latex]\langle -\infty,-1\rangle \cup \langle 0,+\infty\rangle[/latex]. To je čisto zato što je skup rješenja nejednadžbe [latex]x^2+x>0[/latex] unija dva disjunktna skupa.
I za kraj ću dati još jedan primjer koji u sebi sadrži uniju i presjek: [latex]\log (x^2+x)+\frac{1}{x-5}[/latex]. Sada je [latex]U_1=\langle -\infty,-1\rangle \cup \langle 0,+\infty\rangle[/latex] (skup generiran uvjetom logaritma), a [latex]U_2=\mathbb{R}\setminus\{5\}[/latex]. No, završno rješenje je uvijek dobiveno presjekom (osim, naravno, kad imamo samo jedan uvjet, to je možda ovaj slučaj koji tebe najviše buni), iako "izgleda" kao unija: prirodna domena ove funkcije je [latex]U_1\cap U_2=\langle -\infty,-1\rangle \cup \langle 0, 5\rangle\cup \langle 5,+\infty\rangle[/latex].
Nadam se da je bilo barem djelomično shvatljivo :).
Luuka, vidio sam tvoj post, ali sam već bio pri kraju svojeg, pa sam ga ipak odlučio poslati. Thanks anyway :).
@niveus: Ima tu jedan stari trik: naprosto pitaš asistenta  . (A i, kad se traži inverzna funkcija, obično piše nešto u stilu "Odredi . (A i, kad se traži inverzna funkcija, obično piše nešto u stilu "Odredi 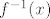 .", a kad se traži praslika, zna pisati nešto u stilu "Odredi .", a kad se traži praslika, zna pisati nešto u stilu "Odredi 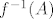 .", gdje je .", gdje je  neki skup. Ali ja bih se ipak držao prokušanog trika s asistentom neki skup. Ali ja bih se ipak držao prokušanog trika s asistentom  .) .)
@kykica: U načelu, izgled prirodne domene uvijek je oblika  , gdje je , gdje je 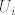 "prihvatljiva" domena za i-ti uvjet. Jesam malo neprecizan, ali mislim da ćeš shvatiti "prihvatljiva" domena za i-ti uvjet. Jesam malo neprecizan, ali mislim da ćeš shvatiti  . Na primjer, funkcija . Na primjer, funkcija 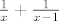 ima prvi uvjet ima prvi uvjet 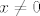 , pa je , pa je 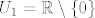 , a drugi uvjet , a drugi uvjet 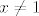 , pa je , pa je 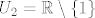 . Sada je prirodna domena . Sada je prirodna domena 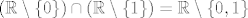 . .
No, ono što tebe vjerojatno zbunjuje je da neki od tih skupova 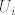 mogu biti unije same po sebi. Na primjer, ako tražiš prirodnu domenu funkcije mogu biti unije same po sebi. Na primjer, ako tražiš prirodnu domenu funkcije 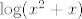 , onda je ona , onda je ona 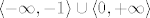 . To je čisto zato što je skup rješenja nejednadžbe . To je čisto zato što je skup rješenja nejednadžbe 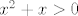 unija dva disjunktna skupa. unija dva disjunktna skupa.
I za kraj ću dati još jedan primjer koji u sebi sadrži uniju i presjek: 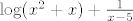 . Sada je . Sada je 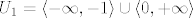 (skup generiran uvjetom logaritma), a (skup generiran uvjetom logaritma), a 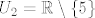 . No, završno rješenje je uvijek dobiveno presjekom (osim, naravno, kad imamo samo jedan uvjet, to je možda ovaj slučaj koji tebe najviše buni), iako "izgleda" kao unija: prirodna domena ove funkcije je . No, završno rješenje je uvijek dobiveno presjekom (osim, naravno, kad imamo samo jedan uvjet, to je možda ovaj slučaj koji tebe najviše buni), iako "izgleda" kao unija: prirodna domena ove funkcije je 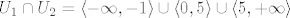 . .
Nadam se da je bilo barem djelomično shvatljivo  . .
Luuka, vidio sam tvoj post, ali sam već bio pri kraju svojeg, pa sam ga ipak odlučio poslati. Thanks anyway  . .
|








