| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 15:40 čet, 5. 11. 2009 Naslov: Re: kolokviji.... Postano: 15:40 čet, 5. 11. 2009 Naslov: Re: kolokviji.... |
    |
|
|
[quote="maty321"]Neka je M = {p ∈ P3; p(1) = p(−1) = 0}. Odredite (jednu) bazu nekog direktnog
komplementa potprostora M u P3[/quote]
[latex]M=\{ p\in \mathcal{P}_3|p(1)=p(-1)=0\}[/latex]
baza za [latex]M[/latex]?
neka je [latex]p\in M[/latex]
[latex]p(t)=a+bt+ct^2+dt^3[/latex]
[latex]p(1)=p(-1)=0\Longrightarrow[/latex]
[latex]\displaystyle \left\{ \begin{array}{l}
a+b+c+d=0\\
a-b+c-d=0\end{array}[/latex]
to se trivijalno rjesi, pa imas
[latex]c=-a \wedge d=-b[/latex]
dakle [latex]p(t)=a+bt-at^2-bt^3=a\left(1-t^2\right)+b\left(t-t^3\right)[/latex]
baza za [latex]M[/latex] je [latex]\{ 1-t^2, t-t^3\}[/latex], to nadopunis do baze za [latex]\mathcal{P}_3[/latex], odnosno nadopunis nekom bazom za [latex]\mathcal{P}_3[/latex], pa reduciras, ono sto ostane a nije iz [latex]M[/latex] je baza za direktan komplement
ako nadopunis sa [latex]\{ 1,t,t^2,t^3 \}[/latex], mislim da ostanu [latex]\{ 1, t\}[/latex], ali ako ostanu i recimo [latex]\{ t^2,t^3\}[/latex] isto je dobro, nije li to predivno, ova dva su si medusobno direktan komplement, a ujedno su direktan komplenet od [latex]M[/latex]
nadam se da je ok... nisam bas raspisivao
| maty321 (napisa): | Neka je M = {p ∈ P3; p(1) = p(−1) = 0}. Odredite (jednu) bazu nekog direktnog
komplementa potprostora M u P3 |

baza za  ? ?
neka je 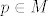
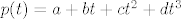
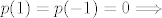
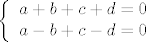
to se trivijalno rjesi, pa imas
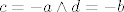
dakle 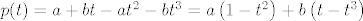
baza za  je je 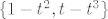 , to nadopunis do baze za , to nadopunis do baze za 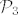 , odnosno nadopunis nekom bazom za , odnosno nadopunis nekom bazom za 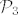 , pa reduciras, ono sto ostane a nije iz , pa reduciras, ono sto ostane a nije iz  je baza za direktan komplement je baza za direktan komplement
ako nadopunis sa 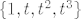 , mislim da ostanu , mislim da ostanu 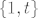 , ali ako ostanu i recimo , ali ako ostanu i recimo 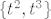 isto je dobro, nije li to predivno, ova dva su si medusobno direktan komplement, a ujedno su direktan komplenet od isto je dobro, nije li to predivno, ova dva su si medusobno direktan komplement, a ujedno su direktan komplenet od 
nadam se da je ok... nisam bas raspisivao
_________________
Mario Berljafa
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 15:49 čet, 5. 11. 2009 Naslov: Postano: 15:49 čet, 5. 11. 2009 Naslov: |
    |
|
|
nije potprostor, inace reko sam vise puta na demonstraturama, asistenti su dobri, nece vam dat zadatak koji ima a i b dio, i ocekivat od vas da svaki od tih raspisujete 2 stranice
bar mi se cini da je tako bilo do sad :D
uglavnom da bi nesto bilo potprostor, mora bit vektorski prostor, pa moraju bit zadovoljeni onih 8 definicjonih svojstva, pokazalo se da je to ekvivalentno sa time da je zatvoren na zbrajanje i mnozenje skalarima, sto koristite u onom raspisivanju na dvije strane
u ovom djelu se lako moze pokazat i sa time da ovo nije vektorski prostor, ali je jos lakse sjetiti se jednog od onih 8 svojstva, npr onaj koji kaze da postoji 0
da li je 0 u unom prostoru?
nije potprostor, inace reko sam vise puta na demonstraturama, asistenti su dobri, nece vam dat zadatak koji ima a i b dio, i ocekivat od vas da svaki od tih raspisujete 2 stranice
bar mi se cini da je tako bilo do sad 
uglavnom da bi nesto bilo potprostor, mora bit vektorski prostor, pa moraju bit zadovoljeni onih 8 definicjonih svojstva, pokazalo se da je to ekvivalentno sa time da je zatvoren na zbrajanje i mnozenje skalarima, sto koristite u onom raspisivanju na dvije strane
u ovom djelu se lako moze pokazat i sa time da ovo nije vektorski prostor, ali je jos lakse sjetiti se jednog od onih 8 svojstva, npr onaj koji kaze da postoji 0
da li je 0 u unom prostoru?
_________________
Mario Berljafa
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 20:55 pet, 6. 11. 2009 Naslov: Postano: 20:55 pet, 6. 11. 2009 Naslov: |
    |
|
|
evo jedan primjer, mislim da takvih nisam vidio na kolokviju jer su pre laki za nac kontraprimjer, al svejedno, uvijek spominjem taj nulvektor, pa da vidite da ne pali uvijek
kao pitanje bi bilo je li [latex]\left\{\left( x,y,z\right)\in\mathbb{R}^3|x+y\leq 3\right \}[/latex] vektorski prostor?
evo jedan primjer, mislim da takvih nisam vidio na kolokviju jer su pre laki za nac kontraprimjer, al svejedno, uvijek spominjem taj nulvektor, pa da vidite da ne pali uvijek
kao pitanje bi bilo je li 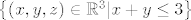 vektorski prostor? vektorski prostor?
_________________
Mario Berljafa
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 13:13 sub, 7. 11. 2009 Naslov: Postano: 13:13 sub, 7. 11. 2009 Naslov: |
    |
|
|
[quote="A_je_to"]Zamolio bi da mi netko riješi 4. zadatak. Hvala!
[url=http://web.math.hr/nastava/la/kolokviji/08_09/kol1b.pdf]kolokvij[/url][/quote]
vektori su nekomplanarni u V3(O) akko su baza,tj.ako su linearno nezavisni:
ovdje je
a=(1,1,p), b=(-1,1,-1), c=(3,p,1) i sada gledaš za koje alfa,beta i gama sustav
alfa(1,1,p)+beta(-1,1,-1)+gama (3,p,1)=(0,0,0) ima samo trivijalno rješenje,tj alfa=beta=gama=0
to nadam se znaš! :)
s drugim dijelom nisam baš načisto,tj.nisam sigurna u rješenje,pa ga neću ni pisati dok ne provjerim...pretpostavljam da treba u a=(1,1,p), b=(-1,1,-1), c=(3,p,1) uvrstiti p za koji/koje si dobio da gornje ne vrijedi, i prikazat d pomoću takvih a,b,i c,ali me malo buni ova komplanarnost..
| A_je_to (napisa): | Zamolio bi da mi netko riješi 4. zadatak. Hvala!
kolokvij |
vektori su nekomplanarni u V3(O) akko su baza,tj.ako su linearno nezavisni:
ovdje je
a=(1,1,p), b=(-1,1,-1), c=(3,p,1) i sada gledaš za koje alfa,beta i gama sustav
alfa(1,1,p)+beta(-1,1,-1)+gama (3,p,1)=(0,0,0) ima samo trivijalno rješenje,tj alfa=beta=gama=0
to nadam se znaš! 
s drugim dijelom nisam baš načisto,tj.nisam sigurna u rješenje,pa ga neću ni pisati dok ne provjerim...pretpostavljam da treba u a=(1,1,p), b=(-1,1,-1), c=(3,p,1) uvrstiti p za koji/koje si dobio da gornje ne vrijedi, i prikazat d pomoću takvih a,b,i c,ali me malo buni ova komplanarnost..
|
|
| [Vrh] |
|
Gergonne
Gost
|
 Postano: 13:56 sub, 7. 11. 2009 Naslov: Postano: 13:56 sub, 7. 11. 2009 Naslov: |
    |
|
|
Zadani vektori su komplanarni akko je p = 1. Zbog toga u drugom dijelu zadatka zapravo treba ispitati za koji se realan broj alfa vektor d = (alfa, -1, 1) može prikazati kao linearna kombinacija vektora a = (1, 1, -1), b = (-1, 1, -1) i c = (3, -1, 1).
U pripadnom sustavu linearnih jednadžbi treća jednadžba dobije se tako da se druga pomnoži s (-1), pa zapravo imamo sustav od dvije linearne jednadžbe s tri nepoznanice. Taj sustav ima parametarsko rješenje ((alfa - 2*t-1)/2, (alfa-4*t-1)/2, t), pa zaključujemo da se za svaki realan broj alfa vektor d = (alfa, -1, 1) može prikazati kao linearna kombinacija vektora a = (1, ,1 -1), b = (-1, 1, -1) i c = (3, -1, 1).
Mislim da je zadatak trebalo tako riješiti, ali ako nešto od navedenog nije točno, neka netko napiše ispravak :wink:
Zadani vektori su komplanarni akko je p = 1. Zbog toga u drugom dijelu zadatka zapravo treba ispitati za koji se realan broj alfa vektor d = (alfa, -1, 1) može prikazati kao linearna kombinacija vektora a = (1, 1, -1), b = (-1, 1, -1) i c = (3, -1, 1).
U pripadnom sustavu linearnih jednadžbi treća jednadžba dobije se tako da se druga pomnoži s (-1), pa zapravo imamo sustav od dvije linearne jednadžbe s tri nepoznanice. Taj sustav ima parametarsko rješenje ((alfa - 2*t-1)/2, (alfa-4*t-1)/2, t), pa zaključujemo da se za svaki realan broj alfa vektor d = (alfa, -1, 1) može prikazati kao linearna kombinacija vektora a = (1, ,1 -1), b = (-1, 1, -1) i c = (3, -1, 1).
Mislim da je zadatak trebalo tako riješiti, ali ako nešto od navedenog nije točno, neka netko napiše ispravak 
|
|
| [Vrh] |
|
Gergonne
Gost
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
Gergonne
Gost
|
 Postano: 18:31 sub, 7. 11. 2009 Naslov: Postano: 18:31 sub, 7. 11. 2009 Naslov: |
    |
|
|
Za p = -1 dobiju se vektori a = (1,1,-1), b = (-1,1,-1) i c = (3,-1,1). Nije teško vidjeti da je npr. c = a - 2*b, pa su vektori a, b i c komplanarni.
Za p = 1 dobiju se vektori a = (1, 1, 1), b = (-1, 1, -1) i c = (3, 1, 1) za koje se lako pokaže da su linearno nezavisni, pa nisu komplanarni.
Za p = -1 dobiju se vektori a = (1,1,-1), b = (-1,1,-1) i c = (3,-1,1). Nije teško vidjeti da je npr. c = a - 2*b, pa su vektori a, b i c komplanarni.
Za p = 1 dobiju se vektori a = (1, 1, 1), b = (-1, 1, -1) i c = (3, 1, 1) za koje se lako pokaže da su linearno nezavisni, pa nisu komplanarni.
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 20:20 uto, 10. 11. 2009 Naslov: Postano: 20:20 uto, 10. 11. 2009 Naslov: |
    |
|
|
tih 20 bodova je zapravo 20%
kolokvij nosi 100% :D
dakle u konacnici ti se ti tvoji bodovi podijele sa 4, i tako od 100 dobis 25...
mislim da to rade jer se bolje boduje
pod bolje mislim cak i postenije, ako neko nesto zezne, neku glupu gresku, onda je glupo skinut 1 bod od 5, al mora se(zapravo ne, i nekad ni za to ne skinu) al 1 0d 20 je mozda vec ok...
sad ti je ostalo sigorno jasno, jer sve pise na netu
tih 20 bodova je zapravo 20%
kolokvij nosi 100% 
dakle u konacnici ti se ti tvoji bodovi podijele sa 4, i tako od 100 dobis 25...
mislim da to rade jer se bolje boduje
pod bolje mislim cak i postenije, ako neko nesto zezne, neku glupu gresku, onda je glupo skinut 1 bod od 5, al mora se(zapravo ne, i nekad ni za to ne skinu) al 1 0d 20 je mozda vec ok...
sad ti je ostalo sigorno jasno, jer sve pise na netu
_________________
Mario Berljafa
|
|
| [Vrh] |
|
zekoo
Forumaš(ica)


Pridružen/a: 31. 10. 2009. (22:58:36)
Postovi: (12)16
Spol: 
|
 Postano: 20:43 uto, 10. 11. 2009 Naslov: Postano: 20:43 uto, 10. 11. 2009 Naslov: |
    |
|
|
ne znam dal je to rađeno na vježbama zadnjim jer nisam bila prisutna nažalost, ali ako netko može riješit bila bi jako zahvalna
ugl. M i L potprostori vektorskog prostora R^4 dani redom svojim bazama
{(2,-1,3,-3),(0,1,0,1),(1,1,1,1)} i {(1,-1,1,-1),(3,2,1,0),(0,1,2,3)} Odredite po jednu bazu za M + L i M presjek L.
ne znam dal je to rađeno na vježbama zadnjim jer nisam bila prisutna nažalost, ali ako netko može riješit bila bi jako zahvalna
ugl. M i L potprostori vektorskog prostora R^4 dani redom svojim bazama
{(2,-1,3,-3),(0,1,0,1),(1,1,1,1)} i {(1,-1,1,-1),(3,2,1,0),(0,1,2,3)} Odredite po jednu bazu za M + L i M presjek L.
_________________
Have no fear of perfection - you'll never reach it.
Salvador Dali
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 20:54 uto, 10. 11. 2009 Naslov: Postano: 20:54 uto, 10. 11. 2009 Naslov: |
    |
|
|
[quote="Gino"]tih 20 bodova je zapravo 20%
kolokvij nosi 100% :D
dakle u konacnici ti se ti tvoji bodovi podijele sa 4, i tako od 100 dobis 25...
mislim da to rade jer se bolje boduje
pod bolje mislim cak i postenije, ako neko nesto zezne, neku glupu gresku, onda je glupo skinut 1 bod od 5, al mora se(zapravo ne, i nekad ni za to ne skinu) al 1 0d 20 je mozda vec ok...
sad ti je ostalo sigorno jasno, jer sve pise na netu[/quote]
hehe hvala puno, nisam to znao, to je baš fora, dobra ideja :)
| Gino (napisa): | tih 20 bodova je zapravo 20%
kolokvij nosi 100% 
dakle u konacnici ti se ti tvoji bodovi podijele sa 4, i tako od 100 dobis 25...
mislim da to rade jer se bolje boduje
pod bolje mislim cak i postenije, ako neko nesto zezne, neku glupu gresku, onda je glupo skinut 1 bod od 5, al mora se(zapravo ne, i nekad ni za to ne skinu) al 1 0d 20 je mozda vec ok...
sad ti je ostalo sigorno jasno, jer sve pise na netu |
hehe hvala puno, nisam to znao, to je baš fora, dobra ideja 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 22:45 uto, 10. 11. 2009 Naslov: Postano: 22:45 uto, 10. 11. 2009 Naslov: |
    |
|
|
Neka su M i L potprostori vektorskog prostora R4 dani, redom, svojim bazama
{(1, 0, 1,−2), (0, 1, 0, 1)} i {(1,−1,−2, 0), (0, 2, 3,−1)}.
Odredite po jednu bazu za M + L i M presjek L.
Evo, kolokvij iz `05.
Dobila sam da je baza za M+L {(1, 0, 1,−2), (0, 1, 0, 1), (1,−1,−2, 0)}
dim(M+L)=3,pa bi dim(M presjek L) trebala biti jednaka 1.
Ali kad tražim bazu za M presjek L dobijem:
(0, 2, 3,−1)=2(1, 0, 1,−2)+ 3(0, 1, 0, 1) + (-1)(1,−1,−2, 0)
i sad bih trebala izbaciti (-1)(1,−1,−2, 0) jer je iz L kao i (0, 2, 3,−1),ali izbacim li ga dobit cu da je dim(M presjek L)=2 što ne bih trebala ???
Zbunjuje me to,ne znam gdje griješim?
Neka su M i L potprostori vektorskog prostora R4 dani, redom, svojim bazama
{(1, 0, 1,−2), (0, 1, 0, 1)} i {(1,−1,−2, 0), (0, 2, 3,−1)}.
Odredite po jednu bazu za M + L i M presjek L.
Evo, kolokvij iz `05.
Dobila sam da je baza za M+L {(1, 0, 1,−2), (0, 1, 0, 1), (1,−1,−2, 0)}
dim(M+L)=3,pa bi dim(M presjek L) trebala biti jednaka 1.
Ali kad tražim bazu za M presjek L dobijem:
(0, 2, 3,−1)=2(1, 0, 1,−2)+ 3(0, 1, 0, 1) + (-1)(1,−1,−2, 0)
i sad bih trebala izbaciti (-1)(1,−1,−2, 0) jer je iz L kao i (0, 2, 3,−1),ali izbacim li ga dobit cu da je dim(M presjek L)=2 što ne bih trebala ???
Zbunjuje me to,ne znam gdje griješim?
|
|
| [Vrh] |
|
|







