| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 18:16 sub, 24. 10. 2009 Naslov: karakterizacija neprekidnosti Postano: 18:16 sub, 24. 10. 2009 Naslov: karakterizacija neprekidnosti |
    |
|
|
na vježbama smo napisali:
(uz [latex]A \subseteq \mathbb{R}^n, f:A \rightarrow \mathbb{R}^k [/latex])
funkcija [latex]f[/latex] je neprekidna ako i samo ako za svaki otvoren podskup u kodomeni [latex]U \subseteq \mathbb{R}^k[/latex] je [latex]f^{-1}(U)[/latex] otvoren u [latex]A[/latex], tj postoji otvoren skup [latex]V \subseteq \mathbb{R}^n[/latex] td je [latex]f^{-1}(U) = A \cap V[/latex]
e sad, zbunjuje me zašto uzimamo otvorene podskupove [latex]U[/latex] iz [b]cijele[/b] kodomene, a ne samo iz slike funkcije [latex]f[/latex]?
jer što ako f nije surjektivna? tada slika od f nije jednaka kodomeni (npr. [latex]\mathbb{R}^k[/latex]), odnosno [latex]Im f \neq \mathbb{R}^k[/latex], a to znači da možemo uzeti neki otvoren podskup [latex]B[/latex] iz kodomene koji je disjunktan sa slikom funkcije, odnosno koji nema prasliku po funkciji [latex]f[/latex]. a funkcija može biti cijelo vrijeme neprekidna :?
isti je iskaz i u skripti ([url=http://web.math.hr/nastava/difraf/dif/p_o6.pdf]klik[/url] napomena 6.13): uzima se svaki otvoren podskup baš od cijelog [latex]\mathbb{R}^k[/latex]...
i za kraj, bio bih zahvalan za ideju kako dokazati ovu karakterizaciju, tj. [latex]f[/latex] neprekidna [latex]\Leftrightarrow[/latex] praslika svakog otvorenog skupa iz kodomene je otvoren u domeni. nešt sam pokušavao sa def neprekidnosti i def otvorenog skupa ali nije mi baš išlo :|
zahvaljujem na pomoći! :)
na vježbama smo napisali:
(uz 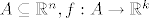 ) )
funkcija  je neprekidna ako i samo ako za svaki otvoren podskup u kodomeni je neprekidna ako i samo ako za svaki otvoren podskup u kodomeni  je je 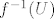 otvoren u otvoren u  , tj postoji otvoren skup , tj postoji otvoren skup  td je td je 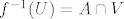
e sad, zbunjuje me zašto uzimamo otvorene podskupove 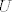 iz cijele kodomene, a ne samo iz slike funkcije iz cijele kodomene, a ne samo iz slike funkcije  ? ?
jer što ako f nije surjektivna? tada slika od f nije jednaka kodomeni (npr. 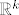 ), odnosno ), odnosno 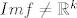 , a to znači da možemo uzeti neki otvoren podskup , a to znači da možemo uzeti neki otvoren podskup  iz kodomene koji je disjunktan sa slikom funkcije, odnosno koji nema prasliku po funkciji iz kodomene koji je disjunktan sa slikom funkcije, odnosno koji nema prasliku po funkciji  . a funkcija može biti cijelo vrijeme neprekidna . a funkcija može biti cijelo vrijeme neprekidna 
isti je iskaz i u skripti (klik napomena 6.13): uzima se svaki otvoren podskup baš od cijelog 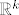 ... ...
i za kraj, bio bih zahvalan za ideju kako dokazati ovu karakterizaciju, tj.  neprekidna neprekidna  praslika svakog otvorenog skupa iz kodomene je otvoren u domeni. nešt sam pokušavao sa def neprekidnosti i def otvorenog skupa ali nije mi baš išlo praslika svakog otvorenog skupa iz kodomene je otvoren u domeni. nešt sam pokušavao sa def neprekidnosti i def otvorenog skupa ali nije mi baš išlo 
zahvaljujem na pomoći! 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:25 sub, 24. 10. 2009 Naslov: Postano: 19:25 sub, 24. 10. 2009 Naslov: |
    |
|
|
Ovo što piše da je [latex]U \subseteq R^n[/latex] bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga.
Prvi smjer, ukoliko je funckija neprekidna, izaberemo neki otovren skup slike funkcije i pokažemo da je njegova praslika također otvorena. To pokazujemo koristeći neprekidnost funkcije i definiciju otovrenog skupa.
U drugom smjeru, pretpostavimo da je praslika svakog otvorenog intervala otvorena i da funkcija nije neprekidna. Sada to lako dovodimo do kontradikcije.
Ovo što piše da je  bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga. bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga.
Prvi smjer, ukoliko je funckija neprekidna, izaberemo neki otovren skup slike funkcije i pokažemo da je njegova praslika također otvorena. To pokazujemo koristeći neprekidnost funkcije i definiciju otovrenog skupa.
U drugom smjeru, pretpostavimo da je praslika svakog otvorenog intervala otvorena i da funkcija nije neprekidna. Sada to lako dovodimo do kontradikcije.
|
|
| [Vrh] |
|
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 19:40 sub, 24. 10. 2009 Naslov: Postano: 19:40 sub, 24. 10. 2009 Naslov: |
    |
|
|
[quote="JANKRI"]Ovo što piše da je [latex]U \subseteq R^n[/latex] bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga.[/quote]
ahaaa! :idea: :D
[quote="JANKRI"]Prvi smjer, ukoliko je funckija neprekidna, izaberemo neki otovren skup slike funkcije i pokažemo da je njegova praslika također otvorena. To pokazujemo koristeći neprekidnost funkcije i definiciju otovrenog skupa.
U drugom smjeru, pretpostavimo da je praslika svakog otvorenog intervala otvorena i da funkcija nije neprekidna. Sada to lako dovodimo do kontradikcije.[/quote]
puno hvala! :karma:
| JANKRI (napisa): | Ovo što piše da je  bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga. bilo koji otvoren nam ne predstavlja probleme, ukoliko on nema zajedničkih točki sa slikom funkcija, njegova praslika je prazan skup, što je otvoreno. Također, ukoliko ima samo neke točke zajedničke sa slikom, onda promatramo samo te točke, a preostale nam ne smetaju iz istog razloga. |
ahaaa!  
| JANKRI (napisa): | Prvi smjer, ukoliko je funckija neprekidna, izaberemo neki otovren skup slike funkcije i pokažemo da je njegova praslika također otvorena. To pokazujemo koristeći neprekidnost funkcije i definiciju otovrenog skupa.
U drugom smjeru, pretpostavimo da je praslika svakog otvorenog intervala otvorena i da funkcija nije neprekidna. Sada to lako dovodimo do kontradikcije. |
puno hvala! 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 2:40 ned, 1. 11. 2009 Naslov: Postano: 2:40 ned, 1. 11. 2009 Naslov: |
    |
|
|
Ajde da ja onda to LaTeX-iram :D
[b]Prvi smjer.[/b]
Neka je [latex]f : A \subseteq \mathbb{R}^n \to \mathbb{R}^k[/latex] neprekidna funkcija. Želimo pokazati da za svaki otvoreni [latex]U \subseteq \mathbb{R}^k[/latex] postoji otvoreni [latex]V \subseteq \mathbb{R}^n[/latex] takav da je [latex]f^{-1}\left(U\right) = V \cap A[/latex].
Ukoliko je [latex]f^{-1}\left(U\right) = \emptyset[/latex] tvrdnja trivijalno vrijedi za [latex]V = \emptyset[/latex]. Neka je dalje [latex]B = f^{-1}\left(U\right) \neq \emptyset[/latex]. Funkcija [latex]f[/latex] je neprekidna na [latex]A[/latex], a time i na [latex]B \subseteq A[/latex], odnosno
[latex]\forall x \in B,\ \forall \varepsilon \in \left\langle0,\, \lambda_x\right\rangle,\ \exists \delta_x >0,\ \left(f\left(A \cap K\left(x,\, \delta_x\right) \setminus \left\{x\right\}\right) \subseteq K\left(f\left(x\right),\, \varepsilon\right) \subseteq U\right)[/latex]. Ovdje je [latex]\lambda_x = \sup{\left\{\epsilon : \epsilon > 0,\, K\left(f\left(x\right),\, \epsilon\right) \subseteq U\right\}[/latex]. Prihvaćamo da taj supremum bude jednak i [latex]+\infty[/latex], ali znamo da je on uvijek strogo pozitivan, jer je skup [latex]U[/latex] otvoren pa oko svake njegove točke postoji neka otvorena kugla cijela sadržana u njemu.
Sada definiramo [latex]V = \bigcup\limits_{x \in B} K\left(x,\, \delta_x\right)[/latex], jasno je da je skup [latex]V[/latex] otvoren (unija familije otvorenih skupova). Pošto je [latex]A \cap K\left(x,\, \delta_x\right) \subseteq B,\ \forall x \in B[/latex], dobili smo da je [latex]B = V \cap A[/latex], gdje je [latex]V \subseteq \mathbb{R}^k[/latex] otvoren.
[b]Drugi smjer.[/b]
Neka je [latex]f : A \subseteq \mathbb{R}^n \to \mathbb{R}^k[/latex] takva da [latex]\forall U \subseteq \mathbb{R}^k[/latex] otvoren, [latex]\exists V \subseteq \mathbb{R}^n[/latex] otvoren, tako da je [latex]f^{-1}\left(U\right) = V \cap A[/latex]. Želimo pokazati da je funkcija [latex]f[/latex] neprekidna na [latex]A[/latex], odnosno:
[latex]\forall c \in A,\ \forall \varepsilon > 0,\ \exists \delta > 0,\ \left(f\left(A \cap K\left(c,\, \delta\right) \setminus \left\{c\right\}\rigth) \subseteq K\left(f\left(c\right),\, \varepsilon\right)\right)[/latex].
Jasno je da je [latex]K\left(f\left(c\right),\, \varepsilon\right)[/latex] otvoreno u [latex]\mathbb{R}^k[/latex] pa prema uvjetima teorema postoji otvoren [latex]V \subseteq \mathbb{R}^n[/latex] takav da je [latex]f^{-1}\left(K\left(f\left(c\right),\, \varepsilon\right)\right) = V \cap A[/latex]. Sada vidimo da je dovoljno uzeti takav [latex]\delta > 0[/latex] za koji je [latex]K\left(c,\, \delta\right) \subseteq V[/latex], za njega znamo da postoji jer je skup [latex]V \subseteq \mathbb{R}^n[/latex] otvoren, te [latex]c[/latex] sigurno jedna njegova točka.
Ovime je dokaz završen, nadam se da je jasan i da nema rupa... :D
Možda bi i u jednom i u drugom smjeru posebno trebalo razmatrati izolirane točke, ali oko njih uvijek gledamo kugle koje sadrže samo njih, koje postoje jer su to izolirane točke, pa s time nemamo problema.
Ajde da ja onda to LaTeX-iram 
Prvi smjer.
Neka je 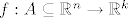 neprekidna funkcija. Želimo pokazati da za svaki otvoreni neprekidna funkcija. Želimo pokazati da za svaki otvoreni  postoji otvoreni postoji otvoreni  takav da je takav da je 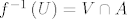 . .
Ukoliko je 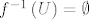 tvrdnja trivijalno vrijedi za tvrdnja trivijalno vrijedi za 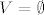 . Neka je dalje . Neka je dalje 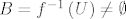 . Funkcija . Funkcija  je neprekidna na je neprekidna na  , a time i na , a time i na 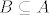 , odnosno , odnosno
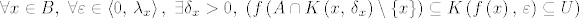 . Ovdje je . Ovdje je 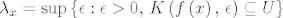 . Prihvaćamo da taj supremum bude jednak i . Prihvaćamo da taj supremum bude jednak i  , ali znamo da je on uvijek strogo pozitivan, jer je skup , ali znamo da je on uvijek strogo pozitivan, jer je skup 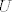 otvoren pa oko svake njegove točke postoji neka otvorena kugla cijela sadržana u njemu. otvoren pa oko svake njegove točke postoji neka otvorena kugla cijela sadržana u njemu.
Sada definiramo 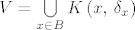 , jasno je da je skup , jasno je da je skup 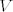 otvoren (unija familije otvorenih skupova). Pošto je otvoren (unija familije otvorenih skupova). Pošto je 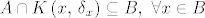 , dobili smo da je , dobili smo da je 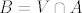 , gdje je , gdje je 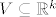 otvoren. otvoren.
Drugi smjer.
Neka je 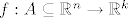 takva da takva da  otvoren, otvoren, 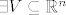 otvoren, tako da je otvoren, tako da je 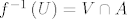 . Želimo pokazati da je funkcija . Želimo pokazati da je funkcija  neprekidna na neprekidna na  , odnosno: , odnosno:
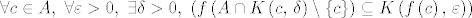 . .
Jasno je da je 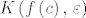 otvoreno u otvoreno u 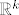 pa prema uvjetima teorema postoji otvoren pa prema uvjetima teorema postoji otvoren  takav da je takav da je 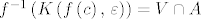 . Sada vidimo da je dovoljno uzeti takav . Sada vidimo da je dovoljno uzeti takav 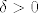 za koji je za koji je 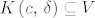 , za njega znamo da postoji jer je skup , za njega znamo da postoji jer je skup  otvoren, te otvoren, te  sigurno jedna njegova točka. sigurno jedna njegova točka.
Ovime je dokaz završen, nadam se da je jasan i da nema rupa... 
Možda bi i u jednom i u drugom smjeru posebno trebalo razmatrati izolirane točke, ali oko njih uvijek gledamo kugle koje sadrže samo njih, koje postoje jer su to izolirane točke, pa s time nemamo problema.
|
|
| [Vrh] |
|
|







