| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:55 pon, 2. 11. 2009 Naslov: Postano: 7:55 pon, 2. 11. 2009 Naslov: |
    |
|
|
Ova funkcija, barem na cijelom [latex]\mathbb{R}[/latex], nije injekcija, ali je injekcija na [latex]\langle -\infty,0][/latex]. Pretpostavljam da te taj interval interesira :).
Dakle, ideja je opet u korištenju kompozicija. Funkcija se očito može prikazati u obliku [latex]f(x)=4^x-3\cdot 2^x=(2^x)^2-3\cdot 2^x[/latex]. Dakle, očito je da je [latex]f[/latex] kompozicija [latex]f_1(x)=x^2-3x[/latex] i [latex]f_2(x)=2^x[/latex]. Sad, pretpostavimo da je [latex]f(x_1)=f(x_2)[/latex]. To znači [latex]f_1(f_2(x_1))=f_1(f_2(x_2))[/latex]. Ako s [latex]y_1[/latex] označimo [latex]f_2(x_1)[/latex], a s [latex]y_2[/latex] označimo [latex]f_2(x_2)[/latex], imamo [latex]f_1(y_1)=f_1(y_2)[/latex]. Sad, mi znamo (zbog funkcije [latex]f_2[/latex]) da su i [latex]y_1[/latex] i [latex]y_2[/latex] pozitivni. Na tom intervalu je funkcija [latex]f_1[/latex] injektivna, pa onda imamo [latex]y_1=y_2[/latex].
Sad smo na kraju puta. Naime, to znači [latex]f_2(x_1)=f_2(x_2)[/latex]. Kako je i [latex]f_2[/latex] injektivna, imamo [latex]x_1=x_2[/latex], što znači da je [latex]f[/latex] injekcija.
Ova funkcija, barem na cijelom  , nije injekcija, ali je injekcija na , nije injekcija, ali je injekcija na 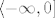 . Pretpostavljam da te taj interval interesira . Pretpostavljam da te taj interval interesira  . .
Dakle, ideja je opet u korištenju kompozicija. Funkcija se očito može prikazati u obliku 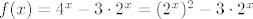 . Dakle, očito je da je . Dakle, očito je da je  kompozicija kompozicija 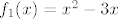 i i 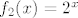 . Sad, pretpostavimo da je . Sad, pretpostavimo da je 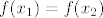 . To znači . To znači 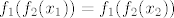 . Ako s . Ako s 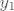 označimo označimo 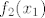 , a s , a s 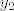 označimo označimo 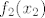 , imamo , imamo 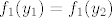 . Sad, mi znamo (zbog funkcije . Sad, mi znamo (zbog funkcije 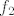 ) da su i ) da su i 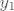 i i 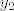 pozitivni. Na tom intervalu je funkcija pozitivni. Na tom intervalu je funkcija 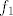 injektivna, pa onda imamo injektivna, pa onda imamo 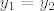 . .
Sad smo na kraju puta. Naime, to znači 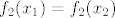 . Kako je i . Kako je i 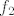 injektivna, imamo injektivna, imamo 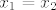 , što znači da je , što znači da je  injekcija. injekcija.
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:28 pon, 2. 11. 2009 Naslov: Postano: 21:28 pon, 2. 11. 2009 Naslov: |
    |
|
|
Da, uz to da treba primijetiti da nije bitno da su obje funkcije strogo monotone na "originalnom" intervalu, nego da je "vanjska" funkcija strogo monotona na intervalu u kojem će biti njeni argumenti.
Na primjer, [latex]f(x)=(\arctan (x-1))^2[/latex] na intervalu [latex][0,+\infty\rangle[/latex] nije injektivna, makar su sve funkcije koje čine kompoziciju injektivne na tom intervalu.
Da, uz to da treba primijetiti da nije bitno da su obje funkcije strogo monotone na "originalnom" intervalu, nego da je "vanjska" funkcija strogo monotona na intervalu u kojem će biti njeni argumenti.
Na primjer, 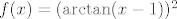 na intervalu na intervalu 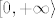 nije injektivna, makar su sve funkcije koje čine kompoziciju injektivne na tom intervalu. nije injektivna, makar su sve funkcije koje čine kompoziciju injektivne na tom intervalu.
|
|
| [Vrh] |
|
|






