| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
 Postano: 22:03 sub, 13. 9. 2008 Naslov: Postano: 22:03 sub, 13. 9. 2008 Naslov: |
    |
|
|
Hvala :D
Evo sad par novih zadataka:
1.Neka je X Hilbertov prostor i P ogranicen, P*P=P. Dokazite
a) Ako P nije 0, onda je ||P||>=1
b) Ako je P ortogonalni projektor, tada je ||P||=1.
2.Neka je H Hilbertov prostor i A ogranicen operator na H. Dokazite da postoje jedinstveni hermitki operatori B,C ograniceni, takvi da je A=B+iC, gdje je i=sqrt(-1). Dokazite da je A normalan ako i samo ako B i C komutiraju.
3.Neka je H Hilbertov prostor sa skalarnim produktom (.|.). Neka je dana familija kompaktnih operatora C_n, koji su elementi od L(X), koja u normi konvergira ka operatoru C. Neka je takodjer dan slabo konvergentan niz vektora x_n t.d. (w) x_n->x_0. Konvergira li niz brojeva (C-nx_n|x_n)? Ako da,pokazite kamo.
4. Neka je Y zatvoren, a Z konacno-dimenzionalan potprostor normiranog prostora X. Tada je potrpostor Y+Z zatvoren. Dokazite!
Unaprijed hvala! :)
[size=9][color=#999999]Added after 1 hours 32 minutes:[/color][/size]
Prva dva ne treba rijesavati, dovrsila sam ih, ali zato imam jedan novi:
Neka su A_n i A neprekinuti linearni hermitski operatori na Hilbretovom prostoru X i x_n i x iz X, takvi da vrijedi A_n->A(s) i x_n->x(w). Konvergira li niz vektora A_nx_n? Ako da, pokazite kamo.
Hvala 
Evo sad par novih zadataka:
1.Neka je X Hilbertov prostor i P ogranicen, P*P=P. Dokazite
a) Ako P nije 0, onda je ||P||>=1
b) Ako je P ortogonalni projektor, tada je ||P||=1.
2.Neka je H Hilbertov prostor i A ogranicen operator na H. Dokazite da postoje jedinstveni hermitki operatori B,C ograniceni, takvi da je A=B+iC, gdje je i=sqrt(-1). Dokazite da je A normalan ako i samo ako B i C komutiraju.
3.Neka je H Hilbertov prostor sa skalarnim produktom (.|.). Neka je dana familija kompaktnih operatora C_n, koji su elementi od L(X), koja u normi konvergira ka operatoru C. Neka je takodjer dan slabo konvergentan niz vektora x_n t.d. (w) x_n→x_0. Konvergira li niz brojeva (C-nx_n|x_n)? Ako da,pokazite kamo.
4. Neka je Y zatvoren, a Z konacno-dimenzionalan potprostor normiranog prostora X. Tada je potrpostor Y+Z zatvoren. Dokazite!
Unaprijed hvala! 
Added after 1 hours 32 minutes:
Prva dva ne treba rijesavati, dovrsila sam ih, ali zato imam jedan novi:
Neka su A_n i A neprekinuti linearni hermitski operatori na Hilbretovom prostoru X i x_n i x iz X, takvi da vrijedi A_n→A(s) i x_n→x(w). Konvergira li niz vektora A_nx_n? Ako da, pokazite kamo.
_________________
' Zasto jednostavno kad moze i komplicirano?'
|
|
| [Vrh] |
|
Felicity
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
popravljac
Forumaš(ica)

Pridružen/a: 20. 02. 2009. (14:05:48)
Postovi: (D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:42 pon, 9. 11. 2009 Naslov: Postano: 20:42 pon, 9. 11. 2009 Naslov: |
    |
|
|
kao prvo, puno je lakše gledat f_n i f_(n+k) za k iz N nego m i n, čisto da su indexi sličniji, a radi se o istoj stvari. :D
A ja sam to ovako nekako:
[latex]|| f_{n+k}- f_n|| = sup | x(1-(n+k)x)\sqrt{n+k} - x(1-nx)\sqrt{n}) | \leq [/latex]
[latex]
\leq sup | x(1-(n+k)x)\sqrt{n+k}|+ sup |x(1-nx)\sqrt{n}) | = ||f_{n+k}|| + ||f_n||[/latex]
Lako dobijemo da je [latex]|| f_n|| = \frac{1}{4 \sqrt{n}}[/latex] (maximum se postiže u tjemenu kv fje, tj u stacionarnoj točki, koja je x=1/(2n)).
Dobijemo:
[latex]|| f_{n+k}- f_n|| \leq \frac{1}{4\sqrt{n+k}} + \frac{1}{4\sqrt{n}} \leq 2 \cdot \frac{1}{4 \sqrt{n}} = \frac{1}{2\sqrt{n}}[/latex]
Dakle za epsilon proizvoljan, uzmemo no naprimjer kao
[latex]n_0 = \lfloor \frac{1}{4 \epsilon^2} \rfloor +1 [/latex]
i za svaki n>=n0, i k iz N vrijedi gornja ocjena s epsilon, dakle niz je Cauchyjev :D
kao prvo, puno je lakše gledat f_n i f_(n+k) za k iz N nego m i n, čisto da su indexi sličniji, a radi se o istoj stvari. 
A ja sam to ovako nekako:
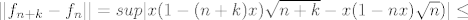
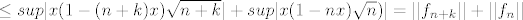
Lako dobijemo da je 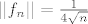 (maximum se postiže u tjemenu kv fje, tj u stacionarnoj točki, koja je x=1/(2n)). (maximum se postiže u tjemenu kv fje, tj u stacionarnoj točki, koja je x=1/(2n)).
Dobijemo:
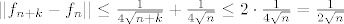
Dakle za epsilon proizvoljan, uzmemo no naprimjer kao
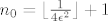
i za svaki n>=n0, i k iz N vrijedi gornja ocjena s epsilon, dakle niz je Cauchyjev 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
popravljac
Forumaš(ica)

Pridružen/a: 20. 02. 2009. (14:05:48)
Postovi: (D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
popravljac
Forumaš(ica)

Pridružen/a: 20. 02. 2009. (14:05:48)
Postovi: (D)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
popravljac
Forumaš(ica)

Pridružen/a: 20. 02. 2009. (14:05:48)
Postovi: (D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
|











