| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 23:53 sub, 7. 11. 2009 Naslov: Potprostor, baza i nadopuna do baze Postano: 23:53 sub, 7. 11. 2009 Naslov: Potprostor, baza i nadopuna do baze |
    |
|
|
Trebala bi pomoc oko zadatka koji glasi ovako:
M={(z1,z2,z3,z4)€C4 : z1+i*z2-z4=0, z1+z3-i*z4=0}.
Treba dokazat da je potprostor, nac bazu i nadopunit bazu do baze za C4.
Trebala bi pomoc oko zadatka koji glasi ovako:
M={(z1,z2,z3,z4)€C4 : z1+i*z2-z4=0, z1+z3-i*z4=0}.
Treba dokazat da je potprostor, nac bazu i nadopunit bazu do baze za C4.
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 1:06 ned, 8. 11. 2009 Naslov: Postano: 1:06 ned, 8. 11. 2009 Naslov: |
    |
|
|
prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
z_1&&&+&z_3&-&iz_4&=&0
\end{array}[/latex]
oduzimanjem dobis
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
&-&iz_2&+&z_3&+&(1-i)z_4&=&0
\end{array}[/latex]
stavis da su [latex]z_2[/latex] i [latex]z_4 [/latex]parametri pa imas
[latex]z_1=-it+s\\
z_2=t\\
z_3=it-(1-i)s\\
z_4=s[/latex]
dakle [latex]z=\left( z_1,z_2,z_3,z_4\right)=\left( -it+s, t, it-(1-i)s,s \right)=t\left( -i,1,i,0\right) +s\left( 1,0,i-1,1\right)[/latex]
pa je baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
treci dio takoder necu pisat....
prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
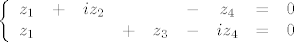
oduzimanjem dobis
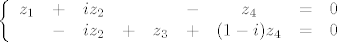
stavis da su 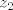 i i 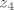 parametri pa imas parametri pa imas
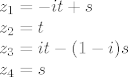
dakle 
pa je baza za  skup skup 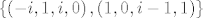
treci dio takoder necu pisat....
_________________
Mario Berljafa
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 23:39 ned, 8. 11. 2009 Naslov: Postano: 23:39 ned, 8. 11. 2009 Naslov: |
    |
|
|
[quote="Gino"]prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
z_1&&&+&z_3&-&iz_4&=&0
\end{array}[/latex]
oduzimanjem dobis
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
&-&iz_2&+&z_3&+&(1-i)z_4&=&0
\end{array}[/latex]
stavis da su [latex]z_2[/latex] i [latex]z_4 [/latex]parametri pa imas
[latex]z_1=-it+s\\
z_2=t\\
z_3=it-(1-i)s\\
z_4=s[/latex]
dakle [latex]z=\left( z_1,z_2,z_3,z_4\right)=\left( -it+s, t, it-(1-i)s,s \right)=t\left( -i,1,i,0\right) +s\left( 1,0,i-1,1\right)[/latex]
pa je baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
treci dio takoder necu pisat....[/quote]
sta to znaci da je nad [latex]\mathbb{C}[/latex], da su skalari iz [latex]\mathbb{C}[/latex]
u tom slucaju ako imas bazu za [latex]\mathbb{C}^4[/latex] recimo kanonsku [latex]\left\{ \left( 1,0,0,0 \right) ,\left( 0,1,0,0\right) ,\left( 0,0,1,0\right) ,\left( 0,0,0,1\right)\right\}[/latex] ocito mozes dobit bilo koji vektor sa tom bazom, ali ako je vektorski prostor izgraden nad poljem realnih brojeva dakle nad [latex]\mathbb{R}[/latex], onda neces nikako moc dobit sve vektore, jer ne mozes mnozit sa npr. [latex]i[/latex], zato ocito ono nije baza za [latex]\mathbb{C}^4[/latex] nad [latex]\mathbb{R}[/latex], ali [latex]\left\{ \left( 1,0,0,0 \right) ,\left( 0,1,0,0\right) ,\left( 0,0,1,0\right) ,\left( 0,0,0,1\right), \left( i,0,0,0 \right) ,\left( 0,i,0,0\right) ,\left( 0,0,i,0\right) ,\left( 0,0,0,i\right)\right\}[/latex] to je, je ok :?:
e sad ako je ono nad [latex]\mathbb{C}[/latex] dodas bazu koju sam naveo za [latex]\mathbb{C}^4[/latex] nad [latex]\mathbb{C}[/latex] i reduciras do baze, moras dobit na koncu [latex]4[/latex] vektora, ako je bio nad [latex]\mathbb{R}[/latex] dodas onu koja ih ima [latex]8[/latex] i reduciras, najnormalnije do baze, koja ce dakle imat [latex]8[/latex] vektora
| Gino (napisa): | prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
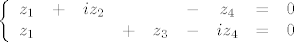
oduzimanjem dobis
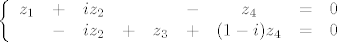
stavis da su 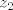 i i 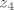 parametri pa imas parametri pa imas
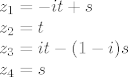
dakle 
pa je baza za  skup skup 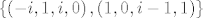
treci dio takoder necu pisat.... |
sta to znaci da je nad  , da su skalari iz , da su skalari iz 
u tom slucaju ako imas bazu za 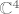 recimo kanonsku recimo kanonsku 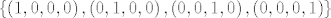 ocito mozes dobit bilo koji vektor sa tom bazom, ali ako je vektorski prostor izgraden nad poljem realnih brojeva dakle nad ocito mozes dobit bilo koji vektor sa tom bazom, ali ako je vektorski prostor izgraden nad poljem realnih brojeva dakle nad  , onda neces nikako moc dobit sve vektore, jer ne mozes mnozit sa npr. , onda neces nikako moc dobit sve vektore, jer ne mozes mnozit sa npr.  , zato ocito ono nije baza za , zato ocito ono nije baza za 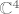 nad nad  , ali , ali 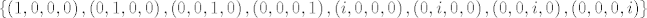 to je, je ok to je, je ok 
e sad ako je ono nad  dodas bazu koju sam naveo za dodas bazu koju sam naveo za 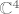 nad nad  i reduciras do baze, moras dobit na koncu i reduciras do baze, moras dobit na koncu 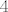 vektora, ako je bio nad vektora, ako je bio nad  dodas onu koja ih ima dodas onu koja ih ima 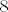 i reduciras, najnormalnije do baze, koja ce dakle imat i reduciras, najnormalnije do baze, koja ce dakle imat 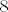 vektora vektora
_________________
Mario Berljafa
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 10:00 pon, 9. 11. 2009 Naslov: Postano: 10:00 pon, 9. 11. 2009 Naslov: |
    |
|
|
U bazu sam dodala obicnu kanonsku bazu..
A(-i,1,i,0)+B(1,0,i-1,1)=(1,0,0,0)
-Ai+B=1
A=0 => B=1
Ai+B(i-1)=0 => i-1=0 => kontradikcija, lin.nezavisni
A(-i,1,i,0)+B(1,0,i-1,1)=(0,1,0,0)
-Ai+B=0
A=1 => B=i
Ai+B(i-1)=0 => -1=0 => kontradikcija
A(-i,1,i,0)+B(1,0,i-1,1)=(0,0,1,0)
-Ai+B=0
A=0 => B=0
Ai+B(i-1)=1 => kontradikcija => kontradikcija
necu dalje pisat, ugl evo, nasla sam ih pet lin nezavisnih??
Jel bi mogo sad molim te napisat kak se to radi ili ti je to prevelki problem?
U bazu sam dodala obicnu kanonsku bazu..
A(-i,1,i,0)+B(1,0,i-1,1)=(1,0,0,0)
-Ai+B=1
A=0 => B=1
Ai+B(i-1)=0 => i-1=0 => kontradikcija, lin.nezavisni
A(-i,1,i,0)+B(1,0,i-1,1)=(0,1,0,0)
-Ai+B=0
A=1 => B=i
Ai+B(i-1)=0 => -1=0 => kontradikcija
A(-i,1,i,0)+B(1,0,i-1,1)=(0,0,1,0)
-Ai+B=0
A=0 => B=0
Ai+B(i-1)=1 => kontradikcija => kontradikcija
necu dalje pisat, ugl evo, nasla sam ih pet lin nezavisnih??
Jel bi mogo sad molim te napisat kak se to radi ili ti je to prevelki problem?
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 10:42 pon, 9. 11. 2009 Naslov: Postano: 10:42 pon, 9. 11. 2009 Naslov: |
    |
|
|
[quote="eve"]Jel bi mogo sad molim te napisat kak se to radi [b]ili ti je to prevelki problem[/b]?[/quote]
da problem je
ja isto imam kolokvije, i zapravo nisam bas radio za vrijeme semestra kako treba, pa moram sad vise nego li sam prosle godine radio u kolokvijsko vrijeme, dobro to nije bitno....
koji god bili razlozi, treba vremena za to raspisat, pogotovo ako se pritom trudis [b]nekulturnim[/b] ljudima zapisat sve u LaTeX-u da bude pregledno,
a kako je pomoc potrebna tebi, logicnije je da ti potrosos na to vise vremena, da si na pocetku napisala odmah ovo reko bi u cemu je problem;
kad nades jednog kojeg ne mozes dobit linearnom kombinacijom ona dva, napr vec prvi kojeg si uzela,
onda kad gledas sljedeceg gledas dal ga mozes dobit linearnom kombinacijom svih prethodnih koji cine linearno nezavisan skup, dakle za onaj drugi vektor kojeg gledas, bi stavila
A(-i,1,i,0)+B(1,0,i-1,1)+[b]C(1,0,0,0)[/b]=(0,1,0,0)
| eve (napisa): | | Jel bi mogo sad molim te napisat kak se to radi ili ti je to prevelki problem? |
da problem je
ja isto imam kolokvije, i zapravo nisam bas radio za vrijeme semestra kako treba, pa moram sad vise nego li sam prosle godine radio u kolokvijsko vrijeme, dobro to nije bitno....
koji god bili razlozi, treba vremena za to raspisat, pogotovo ako se pritom trudis nekulturnim ljudima zapisat sve u LaTeX-u da bude pregledno,
a kako je pomoc potrebna tebi, logicnije je da ti potrosos na to vise vremena, da si na pocetku napisala odmah ovo reko bi u cemu je problem;
kad nades jednog kojeg ne mozes dobit linearnom kombinacijom ona dva, napr vec prvi kojeg si uzela,
onda kad gledas sljedeceg gledas dal ga mozes dobit linearnom kombinacijom svih prethodnih koji cine linearno nezavisan skup, dakle za onaj drugi vektor kojeg gledas, bi stavila
A(-i,1,i,0)+B(1,0,i-1,1)+C(1,0,0,0)=(0,1,0,0)
_________________
Mario Berljafa
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
 Postano: 18:41 uto, 10. 11. 2009 Naslov: Postano: 18:41 uto, 10. 11. 2009 Naslov: |
    |
|
|
jel bi mi mogao netko objasnit nest u vezi zadatka..?zadatak ide ovako:
Neka su L1,...,Ln,B iz R. koje uvjete moraju zadovoljavati ti brojevi da bi M bio potprostor? M={(x1,...,xn):suma Li*xi=B}
i sad, ako je B=0 onda je trivijalno, to kuzim.
a ako je B != 0, onda mi pise da L != 1...pa sad ja ne kuzim zasto L mora biti razlicit od 1..? mislim, ako je L != 1 onda znam dalje, al ne kuzim zasto je tako..pa ako netko moze objasniti..
jel bi mi mogao netko objasnit nest u vezi zadatka..?zadatak ide ovako:
Neka su L1,...,Ln,B iz R. koje uvjete moraju zadovoljavati ti brojevi da bi M bio potprostor? M={(x1,...,xn):suma Li*xi=B}
i sad, ako je B=0 onda je trivijalno, to kuzim.
a ako je B != 0, onda mi pise da L != 1...pa sad ja ne kuzim zasto L mora biti razlicit od 1..? mislim, ako je L != 1 onda znam dalje, al ne kuzim zasto je tako..pa ako netko moze objasniti..
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 19:38 uto, 10. 11. 2009 Naslov: Postano: 19:38 uto, 10. 11. 2009 Naslov: |
    |
|
|
[latex]x,y\in M\\
\alpha ,\beta \in \mathbb{F}[/latex]
sad hocemo da je [latex]\alpha x+\beta y\in M[/latex]
[latex]\alpha x+\beta y=\left( \alpha x_1 + \beta y_1,...,\alpha x_n + \beta y_n\right)\\
\alpha_1\left( \alpha x_1 + \beta y_1\right) +\alpha_2\left( \alpha x_2 + \beta y_2\right)+...+\alpha_n\left( \alpha x_n + \beta y_n\right) =\\
\alpha\left( \alpha_1 x_1+...+\alpha_n x_n\right) + \beta\left( \alpha_1 y_1+...+\alpha_n y_n\right)=\alpha B + \beta B[/latex]
sad zelimo da je [latex]\alpha B + \beta B= B[/latex] sto ocito vrijedi ako je [latex]B=0[/latex], ako [latex]B \neq 0[/latex] onda bi bilo [latex]\alpha + \beta = 1[/latex] al nasi [latex]\alpha[/latex] i [latex]\beta[/latex] su prozovoljno odabrani, mogli su bit recimo [latex]1[/latex] i [latex]2[/latex]
tako da ispada da je jedini uvjet da je [latex]B=0[/latex]
kad [latex]B[/latex] ne bi bio [latex]0[/latex], onda nul vektor ne bi bio u nutra pa ocito da tad ne moze
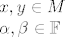
sad hocemo da je 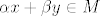
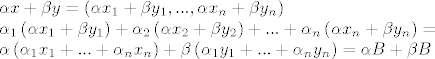
sad zelimo da je 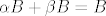 sto ocito vrijedi ako je sto ocito vrijedi ako je 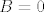 , ako , ako 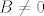 onda bi bilo onda bi bilo 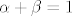 al nasi al nasi  i i 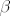 su prozovoljno odabrani, mogli su bit recimo su prozovoljno odabrani, mogli su bit recimo  i i 
tako da ispada da je jedini uvjet da je 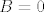
kad  ne bi bio ne bi bio  , onda nul vektor ne bi bio u nutra pa ocito da tad ne moze , onda nul vektor ne bi bio u nutra pa ocito da tad ne moze
_________________
Mario Berljafa
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
 Postano: 0:04 čet, 12. 11. 2009 Naslov: Postano: 0:04 čet, 12. 11. 2009 Naslov: |
    |
|
|
[quote="Gino"]prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
z_1&&&+&z_3&-&iz_4&=&0
\end{array}[/latex]
oduzimanjem dobis
[latex]\left\{ \begin{array}{ccccccccc}
z_1&+&iz_2&&&-&z_4&=&0\\
&-&iz_2&+&z_3&+&(1-i)z_4&=&0
\end{array}[/latex]
stavis da su [latex]z_2[/latex] i [latex]z_4 [/latex]parametri pa imas
[latex]z_1=-it+s\\
z_2=t\\
z_3=it-(1-i)s\\
z_4=s[/latex]
dakle [latex]z=\left( z_1,z_2,z_3,z_4\right)=\left( -it+s, t, it-(1-i)s,s \right)=t\left( -i,1,i,0\right) +s\left( 1,0,i-1,1\right)[/latex]
pa je baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
treci dio takoder necu pisat....[/quote]
sve je ovo okej i rjesila sam do tud:
baza za [latex]M[/latex] skup [latex]\left\{ \left( -i,1,i,0\right) ,\left( 1,0,i-1,1\right)\right\}[/latex]
ali ne kuzim ako smo vec u C zasto onda baza nije (1,0,-1,1)(0,0,i,0)(0,1,0,0)(-i,0,i,0)?????
| Gino (napisa): | prvi dio se nadam da znas, ako ne pogledaj u biljeznicu kako se to radi
sustav cu rjesit
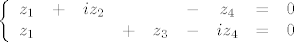
oduzimanjem dobis
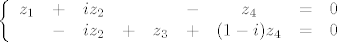
stavis da su 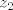 i i 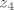 parametri pa imas parametri pa imas
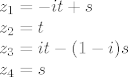
dakle 
pa je baza za  skup skup 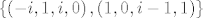
treci dio takoder necu pisat.... |
sve je ovo okej i rjesila sam do tud:
baza za  skup skup 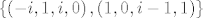
ali ne kuzim ako smo vec u C zasto onda baza nije (1,0,-1,1)(0,0,i,0)(0,1,0,0)(-i,0,i,0)?????
_________________
Give me a place to stand, and I will move the earth.
|
|
| [Vrh] |
|
|















