Sustav u ovisnosti o parametrima (zadatak)

[eve]

Jel može mala pomoć oko zadatka?
Glasi ovak:
Odredite B i C tako da sustav:
x+5y-3z=1
-3x-16y+Bz=2C
2x+12y+8z=1
ima:
a) jedinstveno rješenje
b) beskonačno mnogo rješenja
c) nema rješenja
U slučajevima kada sustav ima rješenja odredite skup rješenja.

**Zbrojila sam 1. i 2., 1. i 3. i dobila:
x+5y-3z=1
-y+z(B-9)=3+2C
2y+14z=-1

Onda sam zbrojila 2. i 3. i dobila sustav:
x+5y-3z=1
2y+14z=-1
2z(B-2)=5+4C

I tu sam zapela...

[Luuka]

Ovako:
prva stvar, stavi sve to u matricu, bit će ti lakše

sustav glasi:


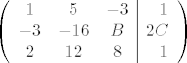
Označimo onu 3x3 matricu sustava sa A.

Sustav će imati jedinstveno rješenje akko je detA!=0.

Ako još nisi radila determinante, onda ovako:
Ovu gore matricu (cijelu, gledaš i desnu stranu), svesti na gornje trokutast oblik. Dakle, elementarnim transformacijama nad retcima poništiti elemente ispod dijagonale. Nakon što dobiješ trokutastu matricu ide diskusija:

1. ako u zadnjem retku imamo 0 0 0 | nešto!=0 sustav nema rješenja
2. ako u zadnjem retku imamo 0 0 0 | 0 sustav ima besk rješenja
3. ako je zadnji redak 0 0 nešto1 | nešto, gdje je nešto1 !=0 onda sustav ima jedinstveno rješenje.

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[eve]

Niš ne kužim nismo radili ni matrice ni determinante...
Daj pliz, ak nije bed da to raspišeš ovak obično...
I, dal je to kaj sam opće radila dobro, potrebno...?

I,da, dobila sam trokutast oblik:
x+5y-3z=1
2y+14z=-1
2z(B-2)=5+4C
ne zgleda tak zbog parametara...

[Luuka]

isto to što si ti radila, se radi i u matrici, samo je puno ljepši zapis i ne izgubiš se tak lako

A došla si do ovog:
x+5y-3z=1
2y+14z=-1
2z(B-2)=5+4C

to bi u matrici bio trukutst oblik (trust me ) i sad idemo sa diskusijom, po slučajevima (zadnji redak == zadnja jednadžba, samo ne gledamo ovaj z):

1. ako 2(B-2)=0, a 5+4C!=0 onda sustav nema rješenja, tj za B=2, C!=-5/4 sustav nema rješenje.
2. ako 2(B-2)=0, i 5+4C=0 onda sustav ima beskonačno rješenja, a to je za B=2, C=-5/4
3. Ako je 2(B-2)!=0 onda sustav ima jedinstaveno rješenje, dakle za B!=2 imamo jedinstveno rješenje

Jel ti treba pomoć oko prikaza rješenja? Samo izraziš x,y i z pomoću B,C i brojeva.

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[eve]

2. ako 2(B-2)=0, i 5+4C=0 onda sustav ima beskonačno rješenja, a to je za B=2, C=-5/4
3. Ako je 2(B-2)!=0 onda sustav ima jedinstaveno rješenje, dakle za B!=2 imamo jedinstveno rješenje

Pod 1. mi je totalno jasno, to sam i pretpostavljala..
2. kužim al nisam sigurna kak iskazat rješenja, jer z je bilo kaj, a x i y se računaju.. ?
a pod 3. nemam blage kak nać rješenje

[Luuka]

pod 2. si dobila 0*z=0, to vrijedi za bilo koji z, pa njega uzmeš kao slobodni parametar.
Iz druge jednadžbe slijedi da je y=(-1 -14z)/2, a iz prve onda da je x=1 -5* (-1-14z)/2 + 3z. Za svaki z iz R će (x,y,z) zadani ovako kako je gore biti rješenje sustava. Očito takvih uređenih trojki ima beskonačno mnogo.

pod 3. slično, samo je 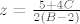i onda opet supsitucije unatrag da dobiješ x i y. To rješenje je jedinstveno

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[eve]

Aaa..kužim..
Fala ti puno!!

Added after 59 minutes:

Još jedno pitanje...
opet isti tip zadatka... ugl, svela sam jednadžbe na:
x+y+6z=1
y+(A-6)z=1
Ay-9z=5
Sad bi trebala ić diskusija...
zanima me da li se gledaju slučajevi kad je A=0 i kad je A!=0, ali i slučajevi kad je A-6=0 i A-6!=0 ?

[Luuka]

[eve]

Da.... a jel onda svejedno trebam gledat kad je A-6=0 i A-6!=0?

[Luuka]

pa i ne baš

jer onda zadnja jednadžba ispadne:
(-A(A-6)-9)z=5-A
ako ja nisam nešt fulo.

A onda je uvjet da je A(A-6)+9 != 0 i svi oni ostali opisani gore

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[miam]

eo tu si to rjesavao..ugl, nest malo ne kuzim..ovo pod 2 i 3 je ok..to kuzim..al, jel nije da bi pod 1 trebalo biti da nema rjesenja i ako je B!=2, a C=-5/4..?

[Luuka]

[miam]

hehe... da
hvala

_________________
<3