|
[quote="piko"]u a) dijelu, da li u svakom koraku pohlepnog algoritma idemo kroz polje i nađemo najmanji element, pa odaberemo njega i manjeg susjeda te ih zbrojimo? ili ide nešto drugo?[/quote]
tako nesto, ja sam konkretno isao ovako, idemo kroz polje proglasimo prva dva kao najpovoljnije, onda idemo dalje i gledamo svaka dva uzastopna, ako naidemo na neke za koje treba manje vremena da se zbroje onda se oni proglase najpovoljnijima, na kraju zbrojimo najpovoljnije i ponovimo postupak dok ne dodemo do niza duljine 1
[quote="piko"]kako dokazati (formalno) da algoritam nađe najmanji broj sekundi?[/quote]
moj algoritam ne nade najmanji broj sekundi, kad bi stavio da ako naide na neki par koji ima isto vrijeme kao i najpovoljniji, i za najpovoljnijeg uzet onaj od ta dva koji daju manji rezultat zbrajanjem onda mozda i bi, al ne bi znao dokazat, a ovako sam naso kontraprimjer :D
11,13,3
algoritam ce zbrojit ovako [latex](11+13)+3[/latex] i utrosit [latex]13+24[/latex] sekundi
ako se zbroji ovako: [latex]11+(13+3)[/latex] trebalo bi [latex]13+16[/latex] sekundi
[quote="piko"]u b), kako izgleda rekurzija[/quote]
[latex]M(p,p)=0[/latex]
[latex]\displaystyle M(p,q\neq p)=\min_{i=0,1,\ldots,q-p-1}\{ M(p,p+i) + M(p+i+1,q) + \max\{ \sum_{k=p}^{p+i}a_k,\sum_{k=p+i+1}^{q}a_k\}\}[/latex]
[quote="piko"]kako bi izgledao traženi program?[/quote]
[code:1]#include <stdio.h>
#include <stdlib.h>
int MAT[100][100]={0};
int a[]={1,4,2,1};
int fmax(int b, int c, int d){
int suma1=0, suma2=0, i;
for(i=b;i<=c;i++) suma1+=a[i];
for(i=c+1;i<=d;i++) suma2+=a[i];
if(suma1>suma2) return suma1;
return suma2;
}
int M(int p, int q){
if(p==q) return 0;
if(p!=q && MAT[p][q]!=0) return MAT[p][q];
int i;
MAT[p][q]=M(p,p)+M(p+1,q)+fmax(p,p,q);//i=0
for(i=1;i<=q-p-1;i++)
if(MAT[p][q]>M(p,p+i)+M(p+i+1,q)+fmax(p,p+i,q))
MAT[p][q]=M(p,p+1)+M(p+i+1,q)+fmax(p,p+i,q);
return MAT[p][q];
}
int main(){
printf("%d",M(0,3));
system("pause");
return 0;
}[/code:1]
| piko (napisa): | | u a) dijelu, da li u svakom koraku pohlepnog algoritma idemo kroz polje i nađemo najmanji element, pa odaberemo njega i manjeg susjeda te ih zbrojimo? ili ide nešto drugo? |
tako nesto, ja sam konkretno isao ovako, idemo kroz polje proglasimo prva dva kao najpovoljnije, onda idemo dalje i gledamo svaka dva uzastopna, ako naidemo na neke za koje treba manje vremena da se zbroje onda se oni proglase najpovoljnijima, na kraju zbrojimo najpovoljnije i ponovimo postupak dok ne dodemo do niza duljine 1
| piko (napisa): | | kako dokazati (formalno) da algoritam nađe najmanji broj sekundi? |
moj algoritam ne nade najmanji broj sekundi, kad bi stavio da ako naide na neki par koji ima isto vrijeme kao i najpovoljniji, i za najpovoljnijeg uzet onaj od ta dva koji daju manji rezultat zbrajanjem onda mozda i bi, al ne bi znao dokazat, a ovako sam naso kontraprimjer 
11,13,3
algoritam ce zbrojit ovako 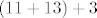 i utrosit i utrosit 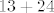 sekundi sekundi
ako se zbroji ovako: 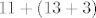 trebalo bi trebalo bi 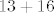 sekundi sekundi
| piko (napisa): | | u b), kako izgleda rekurzija |
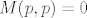
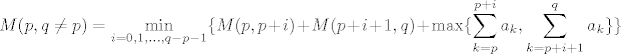
| piko (napisa): | | kako bi izgledao traženi program? |
| Kod: | #include <stdio.h>
#include <stdlib.h>
int MAT[100][100]={0};
int a[]={1,4,2,1};
int fmax(int b, int c, int d){
int suma1=0, suma2=0, i;
for(i=b;i<=c;i++) suma1+=a[i];
for(i=c+1;i<=d;i++) suma2+=a[i];
if(suma1>suma2) return suma1;
return suma2;
}
int M(int p, int q){
if(p==q) return 0;
if(p!=q && MAT[p][q]!=0) return MAT[p][q];
int i;
MAT[p][q]=M(p,p)+M(p+1,q)+fmax(p,p,q);//i=0
for(i=1;i<=q-p-1;i++)
if(MAT[p][q]>M(p,p+i)+M(p+i+1,q)+fmax(p,p+i,q))
MAT[p][q]=M(p,p+1)+M(p+i+1,q)+fmax(p,p+i,q);
return MAT[p][q];
}
int main(){
printf("%d",M(0,3));
system("pause");
return 0;
} |
_________________
Mario Berljafa
|




