| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marijamarija
Forumaš(ica)

Pridružen/a: 14. 11. 2009. (11:59:46)
Postovi: (7)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
 Postano: 14:39 sub, 14. 11. 2009 Naslov: Postano: 14:39 sub, 14. 11. 2009 Naslov: |
    |
|
|
Ak ti nije jasno onda to pojednostavni.
Npr...
(za svaki a,b,c є R ) ((a≤b)Λ(c>0))=> (a•c≤b•c)
(za svaki a,b,c є R ) P=>Q
negacija bi bila:
(Postoji a,b,c є R ) P Λ (ne)Q
(Postoji a,b,c є R ) [(a≤b) Λ (c>0)] Λ (ne)(a•c ≤ b•c)
Odnosno:
(Postoji a,b,c є R ) [(a≤b) Λ (c>0)] Λ (a•c > b•c)
Iako neznam tocno kaj ti nije jasno. Kad negiras onda "za svaki" prelazi u "postoji" i obrnuto.
P.S.
U cem vi kolege forumasi pisete one formule tu na forumu? Mathemathica?
P.P.S.
Jedno potpitanje:
Kako negiramo "postoji tocno jedan"?
Ak ti nije jasno onda to pojednostavni.
Npr...
(za svaki a,b,c є R ) ((a≤b)Λ(c>0))⇒ (a•c≤b•c)
(za svaki a,b,c є R ) P⇒Q
negacija bi bila:
(Postoji a,b,c є R ) P Λ (ne)Q
(Postoji a,b,c є R ) [(a≤b) Λ (c>0)] Λ (ne)(a•c ≤ b•c)
Odnosno:
(Postoji a,b,c є R ) [(a≤b) Λ (c>0)] Λ (a•c > b•c)
Iako neznam tocno kaj ti nije jasno. Kad negiras onda "za svaki" prelazi u "postoji" i obrnuto.
P.S.
U cem vi kolege forumasi pisete one formule tu na forumu? Mathemathica?
P.P.S.
Jedno potpitanje:
Kako negiramo "postoji tocno jedan"?
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
marijamarija
Forumaš(ica)

Pridružen/a: 14. 11. 2009. (11:59:46)
Postovi: (7)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 16:51 sub, 14. 11. 2009 Naslov: Re: kvantifikatori Postano: 16:51 sub, 14. 11. 2009 Naslov: Re: kvantifikatori |
    |
|
|
[quote="marijamarija"]znači kod suprotnog suda ostaje [b]za svaki[/b] .
kod obrata ostaje [b]za svaki[/b]
kod obrata po kontrapoziciji bude:[b]postoji[/b]
kod negacije-jasno-[b]postoji[/b]...
da li sam u pravu?[/quote]
a zašto to tako učiš?
samo slijedi svoju intuiciju.
što je negacija suda:
"svaki student u mojoj grupi ima više od 100 kila."?
pa očito:
"nije istina da svaki student u mojoj grupi ima više od 100 kila.", odnosno, kraće:
"postoji student u mojoj grupi koji nema više od 100 kila.",
tj.
"postoji student u mojoj grupi koji ima manje od 100 kila ili 100 kila.".
[latex](\forall \mathrm{student} \in \mathrm{GRUPA}) (kg(\mathrm{student})>100)[/latex]
negacija toga:
[latex](\exists \mathrm{student} \in \mathrm{GRUPA}) (kg(\mathrm{student}) \leq 100)[/latex]
i onda kad o tome malo dulje razmišljaš, uđe ti u ruku, pa počneš negirati i obrtati po automatizmu.
| marijamarija (napisa): | znači kod suprotnog suda ostaje za svaki .
kod obrata ostaje za svaki
kod obrata po kontrapoziciji bude:postoji
kod negacije-jasno-postoji...
da li sam u pravu? |
a zašto to tako učiš?
samo slijedi svoju intuiciju.
što je negacija suda:
"svaki student u mojoj grupi ima više od 100 kila."?
pa očito:
"nije istina da svaki student u mojoj grupi ima više od 100 kila.", odnosno, kraće:
"postoji student u mojoj grupi koji nema više od 100 kila.",
tj.
"postoji student u mojoj grupi koji ima manje od 100 kila ili 100 kila.".
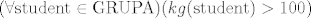
negacija toga:
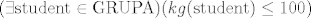
i onda kad o tome malo dulje razmišljaš, uđe ti u ruku, pa počneš negirati i obrtati po automatizmu.
_________________
ima let u finish
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
marijamarija
Forumaš(ica)

Pridružen/a: 14. 11. 2009. (11:59:46)
Postovi: (7)16
|
|
| [Vrh] |
|
Bole13
Forumaš(ica)
Pridružen/a: 01. 11. 2008. (00:33:50)
Postovi: (5A)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
MI
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (20:54:30)
Postovi: (26)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 18:29 ned, 15. 11. 2009 Naslov: Postano: 18:29 ned, 15. 11. 2009 Naslov: |
    |
|
|
[quote="Gino"]kako bi negirali [latex]\exists x \in \mathbb{Z}[/latex] ne sigorno za svaki x koji nije cijeli broj :wink:[/quote]
zašto ne? :?
ako ne vrijedi: [latex]\exists x \in \mathbb{Z}[/latex],
onda vrijedi: [latex]\forall x, x \notin \mathbb{Z}[/latex].
dakle, koji god [latex]x[/latex] uzmem (ma što god on bio), on nije u [latex]\mathbb{Z}[/latex], jer ne postoji [latex]x \in \mathbb{Z}[/latex], tj. [latex]\mathbb{Z}[/latex] je prazan.
[color=orange]edit[/color] ili si ti, Gino, to htio reći?
| Gino (napisa): | kako bi negirali  ne sigorno za svaki x koji nije cijeli broj ne sigorno za svaki x koji nije cijeli broj  |
zašto ne? 
ako ne vrijedi:  , ,
onda vrijedi: 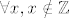 . .
dakle, koji god  uzmem (ma što god on bio), on nije u uzmem (ma što god on bio), on nije u 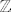 , jer ne postoji , jer ne postoji 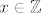 , tj. , tj. 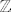 je prazan. je prazan.
edit ili si ti, Gino, to htio reći?
_________________
ima let u finish
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
tperkov
Forumaš(ica)
Pridružen/a: 08. 12. 2008. (15:17:18)
Postovi: (71)16
|
 Postano: 9:14 pon, 16. 11. 2009 Naslov: Postano: 9:14 pon, 16. 11. 2009 Naslov: |
    |
|
|
[quote="Swerz"][quote="Gino"]
nije istina da postoji jedinstveni x>3
odnosno
ili ne postoji niti jedan x>3, ili ih ima vise koji su >3
u negaciji se ne mijenja > u <=
[/quote]
Opet se ne kuzimo. Ajmo treca sreca :wink:
Mozes li ovo gore napisati pomocu kvantifikatora?[/quote]
[latex]\neg\exists !x(x>3)\\
\neg\exists x(x>3) \vee \exists x,y(x\neq y\wedge x,y>3) [/latex]
Drugim riječima, ne postoji x koji je veći od 3 ili postoje dva različita koja su veća od 3
I možda malo elegenatnije, kad iznegiramo prvi dio tvrdnje:
[latex]\forall x(x\leqslant 3) \vee \exists x,y(x\neq y\wedge x,y>3) [/latex]
| Swerz (napisa): | | Gino (napisa): |
nije istina da postoji jedinstveni x>3
odnosno
ili ne postoji niti jedan x>3, ili ih ima vise koji su >3
u negaciji se ne mijenja > u ⇐
|
Opet se ne kuzimo. Ajmo treca sreca 
Mozes li ovo gore napisati pomocu kvantifikatora? |
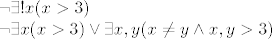
Drugim riječima, ne postoji x koji je veći od 3 ili postoje dva različita koja su veća od 3
I možda malo elegenatnije, kad iznegiramo prvi dio tvrdnje:
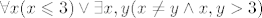
|
|
| [Vrh] |
|
|















