|
[quote="lucijana"]Neka je ø={(x,y): xє R,yє{x-1,x,x+1}}relacija skupa R. Ispitati da li je ona refleksivna,
simetrična, antisimetrična i tranzitivna.[/quote]
refleksivnost ocito vrijedi, naime za [latex]x\in \mathbb{R}[/latex], stavis [latex]y=x[/latex]
[latex]\left( x,y\right) \in \phi \Longrightarrow y\in \left\{ x-1, x, x+1\right\}[/latex]
gledamo sva tri slučaja
[latex]y=x-1 \Longrightarrow \left( y,y+1\right) \in \phi \Longrightarrow \left( y,x\right) \in \phi \\
y=x \Longrightarrow \left( y,y\right) \in \phi \Longrightarrow \left( y,x\right) \in \phi \\
y=x+1 \Longrightarrow \left( y,y-1\right) \in \phi \Longrightarrow \left( y,x\right) \in \phi [/latex]
dakle vrijedi i simetricnost
anitisimetricnost dakako ne,
[latex]\left( x,x+1\right) \in \phi \wedge \left( x+1,\left(x+1\right) -1\right) \in \phi \wedge x\neq x+1[/latex]
takoder ne vrijedi ni tranzitivnost
[latex]\left( x,x+1\right) \in \phi \wedge \left( x+1,x+2\right) \in \phi \wedge \left( x,x+2\right) \notin \phi[/latex]
| lucijana (napisa): | Neka je ø={(x,y): xє R,yє{x-1,x,x+1}}relacija skupa R. Ispitati da li je ona refleksivna,
simetrična, antisimetrična i tranzitivna. |
refleksivnost ocito vrijedi, naime za 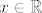 , stavis , stavis 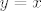
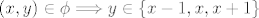
gledamo sva tri slučaja
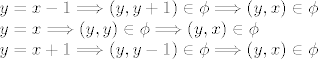
dakle vrijedi i simetricnost
anitisimetricnost dakako ne,
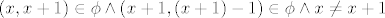
takoder ne vrijedi ni tranzitivnost
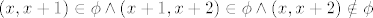
_________________
Mario Berljafa
|






