|
nisam baš siguran da su mi dobro sjeli ovi osnovni pojmovi pa bih bio jako zahvalan ako bi mi netko mogao reći jel ovo valja...
[img]http://i50.tinypic.com/34fjt07.jpg[/img]
u zadatku treba naći diferencijal funkcije [latex]H[/latex] u točki [latex](x,y,z)[/latex], a taj diferencijal [latex]DH(x,y,z)[/latex] je zapravo linearni operator. je li onda dovoljno naći samo [b]matrični zapis[/b] tog linearnog operatora u paru kanonskih baza za[latex] \mathbb{R}^3[/latex] i [latex]\mathbb{R}^2[/latex], odnosno hoće li zadatak biti riješen ako samo nađem Jacobijevu matricu funkcije [latex]H[/latex] u točki [latex](x,y,z)[/latex], tj. [latex]\nabla H (x,y,z)[/latex]?
ako je tako, je li (nakon računanja parcijalnih derivacija)
[latex]\nabla H (x,y,z) =
\left(
\begin{array}{ccc}
e^x+3 x^2 \sin\left(x^3+\frac{\pi z}{2}\right) & 0 & \frac{\pi}{2} \sin}\left(x^3+\frac{\pi z}{2}\right) \\
0 & 4 y z & 2 y^2
\end{array}
\right)[/latex]
rješenje dijela zadatka u kojem se traži da se nađe diferencijal?
dalje treba naći [latex]DH(0,1,1)(1,2,3)[/latex], i tu nisam baš siguran što točno treba.
probao sam ovako: imam matrični zapis linearnog operatora [latex]DH(x,y,z)[/latex], a to je [latex]\nabla H(x,y,z)[/latex]. ako umjesto [latex](x,y,z)[/latex] stavim točku [latex](0,1,1)[/latex], onda dobijem matrični zapis diferencijala funkcije [latex]H[/latex] u točki [latex](0,1,1)[/latex], a to je
[latex]\nabla H (0,1,1)=
\left(
\begin{array}{ccc}
1 & 0 & \frac{\pi}{2} \\
0 & 4 & 2
\end{array}
\right)[/latex]
i sada želim operatorom [latex]DH(0,1,1)[/latex] djelovat na vektor [latex](1,2,3)[/latex], a to je isto kao da pomnožim matricu tog operatora [latex]\nabla H (0,1,1)[/latex] sa vektorom [latex]\left(
\begin{array}{c}
1 \\
2 \\ 3
\end{array}
\right)[/latex], i dobijem [latex]\left(
\begin{array}{c}
1+\frac{3 \pi}{2} \\
14
\end{array}
\right)[/latex], odnosno je li [latex](1+\frac{3 \pi}{2}, 14) \in \mathbb{R}^2[/latex] traženo rješenje?
[img]http://i49.tinypic.com/2d6r3tf.jpg[/img]
derivacija u točki [latex]c[/latex] u smjeru vektora [latex]v[/latex] je limes (ako postoji!) [latex]\mathop {\lim }\limits_{h \to 0 }\frac{f(c+hv)-f(c)}{h}[/latex]
ako označimo [latex]c=(0,0), v= (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})[/latex] onda je
[latex]f(c)=f(0,0) = 0[/latex]
[latex]f(c+hv)=f(\frac{\sqrt{2}}{2}h,\frac{\sqrt{2}}{2}h)=\frac{1}{2 \sqrt{2}}h[/latex] pa je
[latex]\mathop {\lim }\limits_{h \to 0 }\frac{f(c+hv)-f(c)}{h}=
\mathop {\lim }\limits_{h \to 0 }\frac{\frac{1}{2 \sqrt{2}}h}{h}=\frac{1}{2 \sqrt{2}}[/latex]
znači li to da je derivacija funkcije [latex]f[/latex] u točki [latex](0,0)[/latex] u smjeru vektora [latex](\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})[/latex] realan broj [latex]\frac{1}{2 \sqrt{2}}[/latex] ?
unaprijed zahvaljujem! :)
nisam baš siguran da su mi dobro sjeli ovi osnovni pojmovi pa bih bio jako zahvalan ako bi mi netko mogao reći jel ovo valja...

u zadatku treba naći diferencijal funkcije 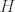 u točki u točki 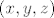 , a taj diferencijal , a taj diferencijal 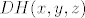 je zapravo linearni operator. je li onda dovoljno naći samo matrični zapis tog linearnog operatora u paru kanonskih baza za je zapravo linearni operator. je li onda dovoljno naći samo matrični zapis tog linearnog operatora u paru kanonskih baza za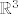 i i 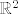 , odnosno hoće li zadatak biti riješen ako samo nađem Jacobijevu matricu funkcije , odnosno hoće li zadatak biti riješen ako samo nađem Jacobijevu matricu funkcije 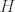 u točki u točki 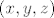 , tj. , tj. 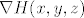 ? ?
ako je tako, je li (nakon računanja parcijalnih derivacija)
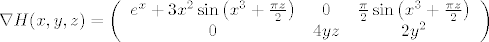
rješenje dijela zadatka u kojem se traži da se nađe diferencijal?
dalje treba naći 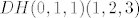 , i tu nisam baš siguran što točno treba. , i tu nisam baš siguran što točno treba.
probao sam ovako: imam matrični zapis linearnog operatora 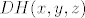 , a to je , a to je 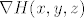 . ako umjesto . ako umjesto 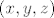 stavim točku stavim točku 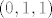 , onda dobijem matrični zapis diferencijala funkcije , onda dobijem matrični zapis diferencijala funkcije 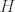 u točki u točki 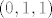 , a to je , a to je
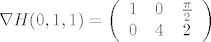
i sada želim operatorom 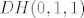 djelovat na vektor djelovat na vektor 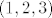 , a to je isto kao da pomnožim matricu tog operatora , a to je isto kao da pomnožim matricu tog operatora 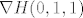 sa vektorom sa vektorom 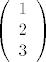 , i dobijem , i dobijem 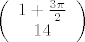 , odnosno je li , odnosno je li 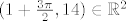 traženo rješenje? traženo rješenje?

derivacija u točki  u smjeru vektora u smjeru vektora  je limes (ako postoji!) je limes (ako postoji!) 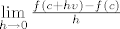
ako označimo 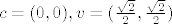 onda je onda je
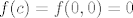
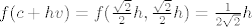 pa je pa je
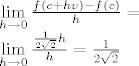
znači li to da je derivacija funkcije  u točki u točki 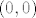 u smjeru vektora u smjeru vektora 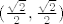 realan broj realan broj 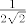 ? ?
unaprijed zahvaljujem! 
|






