6. domaća zadaća

[Tomy007]

Evo da se i ta tema otvori.
Nije mi baš jasno što bi trebao u sljedećem zadatku pa bi molio neki hint : odredite k tako da polinom x^3-9x+k ima dvije nultočke koje su suprotni brojevi.

[Cobs]

neznam, ali vjerojatno ste vec radili iz analize ono crtanje funkcija....

pa bi trebao znati napraviti sljedece:

uzmi funkciju x^3 - 9x

ne trebas si je nacrtati (ali bi ti vjerojatno dosta pomoglo )

trebas nac nul-tocke, stacionarne tocke, podrucje rasta, podrucje pada funkcije, pomocu toga je vec mozes skicirati i kad to ucinis vidjet ces da ako tu funkciju pomaknes za neki broj prema gore ili prema dole dobit ces bas ono sto si trazio ( polinom s 2 razlicite nul tocke ), a onaj broj za koji ces pomaknuti funkciju ti je bas taj k koji trazis

odokativno to bi ti bile vrijednosti funkcije u stacionarnim tockama

( za 2 q - a iz domene ( R ) za koje je f'( q ) = 0 gledas koliki je f( q ) i taj f( q ) = k, mislim da se za razliciti q dobije ista vrijednost drugog predznaka )

[pbakic]

nismo jos crtali funkcije (barem ne s derivacijama, rast-pad itd), al svejedno, cim se stavi f(x)=f(-x) (jer ako su x i -x (suprotni brojevi) nultocke, onda je funkcijska vrijednost u tim tockama ista) i rijesi ta jednadzba, dobije se ovo: (dalje je u bijelom, pa ko zeli... )
(-x)^3-9(-x)+k=x^3-9x+k a iz toga
2x^3-18x=0 Ovo se moze faktorizirati pa dobijes
2x(x-3)(x+3)=0 iz cega jasno vidis da su 0, 3 i -3 jedine tocke za koje je f(x)=f(-x). Ako jos k tome zelimo f(x)=f(-x)=0, uvrstimo ove tocke i pogledamo kakav treba biti k:
za x=3, x=-3 mora biti 3^3-9*3+k=0 iz cega dobivamo k=0
za x=0 (ovo je "rubni" slucaj jer je 0 sama sebi suprotna) takodjer se odmah vidi da je k=0. Iz ovoga zakljucujemo da je jedini moguci k za koji postoje suprotne nultocke upravo 0

[kenny]

Možemo i malo drugačije:

normalni oblik jednadžbe trećeg stupnja je . U ovom je slučaju . Ukoliko pređemo na novu varijablu dobijemo jednadžbu gdje je .

Ubaciš svoje a, b, c, d i dobiješ: .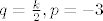

Broj i priroda rješenja ovisi o predznaku determinante . Ukoliko je 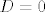jednadžba ima tri realna rješenja (nadam se da je jasno zašto gledamo samo taj slučaj), odnosno podslučaj kad ima dva realna rješenja (jedno realno i dva jednaka realna rješenja): .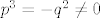

Uvrstiš, središ i dobiješ: .

Nacrtaš tu funkciju u GeoGebri, WolframAlpha i stvarno to dobiješ

p.s. Bronštejn je zlato Hehehehe nisam siguran jeste li ovakav način rješavanja radili na EM1, ali treba se ponekad i malo šire obrazovati, zar ne? Uostalom, ukoliko nije naznačena metoda rješavanja, svaka je dozvoljena

Added after 10 minutes:

Hm, sad mi je palo na pameti i ovo (što je vjerojatno bliže fradivu EM1):

Znaš da funkcija ima dvije realne nultočke koja su različitih predznaka. Dakle, njihov je umnožak strogo negativan: . Pričajmo malo o trećoj nultočki. Ne može biti kompleksna, pa mora biti realna. To bi značilo da postoje tri realne nultočke. Kako je to moguće? Samo ako je jedna nultočka dvostruka. Što znači da polinom možeš zapisati u obliku 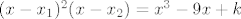. Kvadriraš, središ, izjednačih koeficijente na lijevoj i desnoj strani i dobiješ isto što se dobilo i u postu iznad, samo puno jednostavnije.

Added after 7 minutes:

Evo još jedan način (iako se na kraju sustav svodi na isti koji imaš u postu iznad):

Po Vietovim formulama znamo da za kubne jednadžbe vrijedi


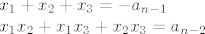
Rasprava je istovjetna onoj raspravi iznad. Dakle, dvije nultočke su jednake. Npr. , pa možemo pisati:


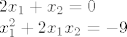
Rješiš sustav. Dobiješ da su ta dva rješenja .

Oba moguća rješenja ubaciš u 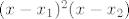, središ i iz toga opet dobiješ dva moguća rješenja za .

_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.

by A.Einstein

[Tomy007]

Hvala svima na pomoći. Ipak mislim da je bakiceva metoda najtocnija sto se tice gradiva em1 jer smo dosad učili samo polinome iz skupa Z i Q, a R još nismo radili.

[maty321]

jel mi moze neko rijesiti ovaj zadatak...zapela sam na jednom dijelu pa..3zadatak..

[miam]

da, stvarno..aj, molim vas da netko rijesi taj 3. zadatak..

_________________
<3

[pbakic]

ovo se rijesi pomocu simetricnih polinoma tri varijable:
umjesto sigma nek bude s1=x+y+z, s2=xy+xz+yz, s3=xyz
sad dani sustav jednadzbi zapisemo pomocu s1, s2, s3

prva jednadzba: s1=-2
druga jednadzba:
sve prebacimo desno, kvadriramo ono, sredimo i dobijemo 0=2s2-9s1
(sad iz toga i iz prve dobijemo s2=-9)
treca jednadzba opet sve bacimo na lijevu stranu i dobijemo
(s3)^2 + 6s3 - 9/2(s1) + s2=0 a kad se uvrste s1 i s2 iz toga nastane
(s3)^2+ 6s3=0 pa imamo dva moguca rjesenja, s3=0 i s3=-6

ovdje se zadatak razdvaja u 2 slucaja vec prema tome koji s3 smo uzeli
prvi: s1=-2, s2=-9, s3=0
sad sastavimo jednadzbu t^3+2t-9t=0
Rjesenja te jednadzbe (u bilo kojoj permutaciji) su (x,y,z).
(Zato sto vieteove formule kazu: ako za x,y,z vrijedi x+y+z=-2 (a to je s1), xy+yz+xz=-9 (s2) i xyz=0 (s3), onda su x,y,z rjesenja ove jednadzbe)

drugi: ista stvar, samo se opredijelimo za slucaj s3=-6 i rijesavamo jednadzbu t^3+2t^2-9t+6=0 (hint: jedno rj. je cijelobrojno)

[Cobs]

nisam ziher za rjesenje....

al ovak sam to radio:

prva se jednadzba uvrsti u drugu i dobije se:

x^2 + y^2 + z^2 = 22

ako kvadriramo prvu jednadzbu dobit cemo:

( x + y + z )^2 = 4

odavde vidimo da je:

2xy + 2xz + 2yz = -18 tj. xy + xz + yz = -9 ( a )

sada ( a ) i prvu jednadzbu ( iz zadatka ) ubacimo u trecu jednadzbu ( iz zadatka )

malo namjestimo i dobijemo:

(xyz)^2 + 6xyz = 0

tj. xyz( xyz + 6 ) = 0

pa imamo:

1) xyz = 0
2) xyz = -6

dalje nisam racunao, ali u slucaju 1)
nisam do kraja provjeravo, mozda je nemoguce, mozda ima rjesenja
uglavnom iz 1) proizlazi da je x ili y ili z = 0, pa ako to uvrstimo u ( a ) vidimo da ostala dva clana pomnozena daju -9, nisam dalje provjeravo jer se to dalje da rjesiti lako,

slucaj 2) u ovom slucaju sam jednadzbu ( a ) mnozio sa jednom od varijabla npr. pomnozim je sa x i dobijem:

xyz + xxy + xxz = -9x sto jee ekvivalentno sa:

x^2( z + y ) = -9x + 6, a iz prve jednadzbe u zadatku dobijem:

z + y = -2 - x i uvrstim u gornju pa dobijem polinom 3. stupnja

sad uocite da cu dobiti isti polinom bez obzira s kojom varijablom sam mnozio u pocetku 2) slucaja. Ta funkcija ima 3 - nultocke, neznam koe jer nisam dalje racunao.

I u prvom slucaju i u drugom dobivene tocke treba provjeriti kroz sve tri jednadzbe.

Kako naci nultocke polinoma 3. stupnja? http://en.wikipedia.org/wiki/Cubic_function

[Genaro]

Zadnji zadatak iz dotične zadaće:

Odredite polinom p stupnja tako da vrijedi:



Molio bih samo konačno rješenje, ako može, radi provjere.

Hvala unaprijed.

[krcko]

Ovako se dobije u Mathematici:

[Genaro]

E super, hvala.

[patlidzan]

A kako se rastavi nazivnik u petom zadatku ?

Hvala

[Altair]

[Genaro]

[patlidzan]

Hvala

[ajaxcy]

Muku mucim s tim zadnjim zadatkkom i i nikako mi ne ispada onako rjesenje....
ima li koja dusa da napise ....

meni ispada a=5 b=-17 c=12 d=0 ???

_________________
Give me a place to stand, and I will move the earth.

[Genaro]

[pajopatak]

A jel zna tko 1. iz zadaće?

[pbakic]

neka je

p(-2)=4, p(5)=7. Sad ih oduzmes i dobijes
p(5)-p(-2)=3 to jest



sad iz svakog ovog izraza oblika 5^k-(-2)^k mozes izlucit (5-(-2)) tj 7, a time dobivas da 7 dijeli lijevu stranu, a desnu ne ⇒ kontradikcija, pa takav polinom ne postoji