|
[quote="patlidzan"]1.Pri dijeljenju polinoma f polinomom g dobije se kvocijent q(x)=x^2+2 i r(x)=4x^3-5x^2-3x+3.
koliki se ostatak dobije pri dijeljenju polinom f polinomom [b]g[/b]?[/quote]
Pretpostavljam da si mislio napisati q, ne g :)
Vrijedi [latex]f(x)=q(x)g(x)+r(x)[/latex]. Podijelimo s [latex]q(x)[/latex]: [latex]\frac{f(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}[/latex].
Dakle, zadatak se svodi da podijeliš [latex]r(x)[/latex] s [latex]q(x)[/latex]. Neka je [latex]r(x)=a(x)q(x)+b(x)[/latex], [latex](st b<st q)[/latex].
Dobimo [latex]\frac{f(x)}{q(x)}=g(x)+a(x)+\frac{b(x)}{q(x)}[/latex]. Pomnožiš s [latex]q(x)[/latex]: [latex]f(x)=(g(x)+a(x))q(x)+b(x)[/latex].
Vidimo da je [latex]b(x)[/latex] traženi ostatak (tm. o dijeljenju polinoma s ostatkom garantira jedinstvenost).
[quote="patlidzan"]2.Odredite sve s,b iz R takve da polinom p(x)=x^4-4x^3+10x^2+ax+b
ima dvije dvostruke nultočke.[/quote]
Rasprava se već vodila [url=http://degiorgi.math.hr/forum/viewtopic.php?t=14230]ovdje[/url].
| patlidzan (napisa): | 1.Pri dijeljenju polinoma f polinomom g dobije se kvocijent q(x)=x^2+2 i r(x)=4x^3-5x^2-3x+3.
koliki se ostatak dobije pri dijeljenju polinom f polinomom g? |
Pretpostavljam da si mislio napisati q, ne g 
Vrijedi 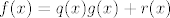 . Podijelimo s . Podijelimo s 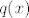 : : 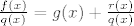 . .
Dakle, zadatak se svodi da podijeliš 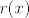 s s 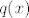 . Neka je . Neka je 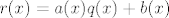 , , 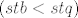 . .
Dobimo 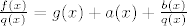 . Pomnožiš s . Pomnožiš s 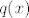 : : 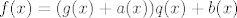 . .
Vidimo da je 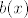 traženi ostatak (tm. o dijeljenju polinoma s ostatkom garantira jedinstvenost). traženi ostatak (tm. o dijeljenju polinoma s ostatkom garantira jedinstvenost).
| patlidzan (napisa): | 2.Odredite sve s,b iz R takve da polinom p(x)=x^4-4x^3+10x^2+ax+b
ima dvije dvostruke nultočke. |
Rasprava se već vodila ovdje.
|






