| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
stips90
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (19:44:43)
Postovi: (9)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 2:10 ned, 17. 1. 2010 Naslov: Postano: 2:10 ned, 17. 1. 2010 Naslov: |
    |
|
|
[quote]2.Što je kompozicija osne simetrije u odnosu na pravac p i centralne simetrije u odnosu na točku T,ako Te p? [/quote]
Odgovor možeš naći negdje u [url=http://degiorgi.math.hr/forum/viewtopic.php?p=129678&highlight=#129678]ovom[/url] mom odgovoru.
[quote]1.Odredite duljine svih stranica trokuta ako su zadana 2 kuta B=50°,Y=60°i duljina dijela simetrale 3.kuta koji leži unutar trokuta sL=10 cm. [/quote]
Dakle, zadan je trokut [latex]\triangle ABC[/latex] i poznato je da je [latex]\beta = 50^o, \gamma = 60^o[/latex]. Lako se izračuna da je [latex]\alpha = 70^o[/latex].
Nacrtaj si trokut i simetralu kuta koja dijeli kut [latex]\alpha[/latex] na dva kuta jednakih veličina. Ta simetrala dijeli trokut na dva manja trokuta. A u svakom je trokutu suma veličine kutova unutar trokuta jednaka. ;) To iskoristi da izračunaš kutove koje zatvara simetrala kuta [latex]\alpha[/latex] sa stranicom [latex]a[/latex].
Na kraju još primjeni sinusov poučak da odrediš duljine stranica trokuta [latex]\triangle ABC[/latex].
[quote]4. Definirajte krnji stožac.[/quote]
Krnji stožac je dio ravnine omeđeno stožastom plohom kojoj su ravnalice dvije zatvorene krivulje čije unutrašnjosti nemaju zajedničkih točaka i ravninama tih ravnalica.
Inače....preporuka....kod definiranja geometrijskih pojmova nacrtaj ono što želiš reći, pa vidi odgovara li tvoja definicija rečenom. Često to koristim u nastavi kad želim da mi klinci sami definiraju nešto...npr. "Što je kružnica?"....obično kažu "Zakrivljena crta", pa ja nacrtam neku zakrivljenu crtu i oni vide da to nije dobro...malo po malo dođu sami do definicije.
| Citat: | | 2.Što je kompozicija osne simetrije u odnosu na pravac p i centralne simetrije u odnosu na točku T,ako Te p? |
Odgovor možeš naći negdje u ovom mom odgovoru.
| Citat: | | 1.Odredite duljine svih stranica trokuta ako su zadana 2 kuta B=50°,Y=60°i duljina dijela simetrale 3.kuta koji leži unutar trokuta sL=10 cm. |
Dakle, zadan je trokut 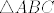 i poznato je da je i poznato je da je 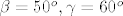 . Lako se izračuna da je . Lako se izračuna da je  . .
Nacrtaj si trokut i simetralu kuta koja dijeli kut  na dva kuta jednakih veličina. Ta simetrala dijeli trokut na dva manja trokuta. A u svakom je trokutu suma veličine kutova unutar trokuta jednaka. na dva kuta jednakih veličina. Ta simetrala dijeli trokut na dva manja trokuta. A u svakom je trokutu suma veličine kutova unutar trokuta jednaka.  To iskoristi da izračunaš kutove koje zatvara simetrala kuta To iskoristi da izračunaš kutove koje zatvara simetrala kuta  sa stranicom sa stranicom  . .
Na kraju još primjeni sinusov poučak da odrediš duljine stranica trokuta 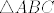 . .
| Citat: | | 4. Definirajte krnji stožac. |
Krnji stožac je dio ravnine omeđeno stožastom plohom kojoj su ravnalice dvije zatvorene krivulje čije unutrašnjosti nemaju zajedničkih točaka i ravninama tih ravnalica.
Inače....preporuka....kod definiranja geometrijskih pojmova nacrtaj ono što želiš reći, pa vidi odgovara li tvoja definicija rečenom. Često to koristim u nastavi kad želim da mi klinci sami definiraju nešto...npr. "Što je kružnica?"....obično kažu "Zakrivljena crta", pa ja nacrtam neku zakrivljenu crtu i oni vide da to nije dobro...malo po malo dođu sami do definicije.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
zada.4
Gost
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 15:36 ned, 17. 1. 2010 Naslov: Postano: 15:36 ned, 17. 1. 2010 Naslov: |
    |
|
|
[quote="teapot"]Iz vrhova A i C pravokutnika ABCD povućene su okomice AP i CQ na dijagonalu BD.Točke P i Q dijele dijagonalu DB na dijelove čije se duljine odnose kao 1:4:1.Ako je duljina dulje stranice pravokutnika 10cm,odredite njegovu površinu.[/quote]
Rečeno je točke [latex]P, Q[/latex] dijele dijagonalu [latex]DB[/latex] u omjeru [latex]1:4:1[/latex], pa možemo pisati: [latex]|DP| = k, |PQ| = 4k, |QB| = k[/latex].
Promotrimo pravokutni trokut [latex]\triangle ABP[/latex] i napišimo relaciju Pitagorinog poučka za taj trokut:
[latex]|AN|^2 = |AP|^2 + |PB|^2 \\
10^2 = |AP|^2 + (5k)^2 \\
|AP|^2 = 100 - 25k^2[/latex]
Promotrimo onda i pravokutni trokut [latex]\triangle APD[/latex] i napišimo za njega relaciju Pitagorinog poučka:
[latex]|AD|^2 = |AP|^2 + |DP|^2 \\
|AD|^2 = (100-25k^2) + k^2 \\
|AD|^2 = 100 - 24k^2[/latex]
Raspišimo još relaciju Pitagorinog poučka za trokut [latex]\triangle ABD[/latex]:
[latex]|AD|^2 + |AB|^2 = |DB|^2 \\
|AD|^2 + 10^2 = (6k)^2 \\
|AD|^2 = 36k^2 - 100[/latex]
Vidimo da možemo pisati (jer je [latex]|AD|^2 = |AD|^2[/latex]):
[latex]100 - 24k^2 = 36k^2-100 \\
-24k^2 - 36k^2 = -100-100 \\
-60k^2 = -200 \\
k^2 = \frac{10}{3} \\
k = \frac{\sqrt{30}}{3}[/latex]
Vratimo se malo unazad gdje smo imali:
[latex]|AD|^2 = 36k^2 - 100 \\
|AD|^2 = 36 \cdot \frac{10}{3} - 100 \\
|AD|^2 = 20 \\
|AD| = 2\sqrt{5}[/latex]
I odgovor...površina tog pravokutnika jednaka je [latex]P = 10 \cdot 2\sqrt{5} = 20 \sqrt{5}[/latex]
[size=9][color=#999999]Added after 23 minutes:[/color][/size]
[quote="zada.4"]Trokut ABC,s kutovima α=20,β=75,γ=85 upisana je kružnica sa središtem O. Neka je K točka na stranici AB takva da je |AK| |BK|=|CK|2 .Dokažite da je OK(okomito) CK.
Ako može netko neka rjesi. Hvala[/quote]
Pretpostavljam da je trokut upisan u kružnicu jer samo tako ima smisla... ;)
Dakle, jedino što mi pada na pamet jest koristiti potenciju točke na kružnici. U ovom slučaju potencije točke [latex]K[/latex] na danu kružnicu.
Podsjetimo prije toga što je potencija kružnice... Neka je dana kružnica [latex]k[/latex] i neka točka [latex]T[/latex] koja ne leži na kružnici. Iz točke [latex]T[/latex] povucimo pravac koji siječe kružnicu [latex]k[/latex] u dvije točke, [latex]U, V[/latex]. Potencija točke [latex]T[/latex] na kružnicu [latex]k[/latex] jest realni broj [latex]|TU| \cdot |TV|[/latex]. Štoviše vrijedi da taj broj ne ovisi o izboru pravca, već samo o izboru točke [latex]T[/latex].
E sad, u zadatku se kaže da je točka [latex]K[/latex] odabrana tako da vrijedi [latex]|AK| \cdot |BK| = |CK|^2[/latex]. Ovdje se zapravo radi o potenciji točke [latex]K[/latex] na kružnicu, ali preko dva različita pravca: preko pravca [latex]AC[/latex] i preko pravca [latex]CK[/latex].
Pogledajmo još i ovo:
[latex]CK \cap k = \{C, D\}[/latex]
A iz relacije potencije točke na kružnicu imamo:
[latex]|AK| \cdot |BK| = |CK|^2 \implies |AK| \cdot |BK| = |CK| \cdot |CK| \\
|AK| \cdot |BK| = |CK| \cdot |DK| \implies |CK| = |DK|[/latex]
Odnosno, točke [latex]K[/latex] je polovište dužine [latex]\overline{CD}[/latex], a [latex]\overline{CD}[/latex] je tetiva zadane kružnice.
I za kraj: znamo da ako promjer kružnice prolazi polovištem tetive, onda je on okomit na tetivu, odnosno - [latex]OK \perp CK[/latex].
| teapot (napisa): | | Iz vrhova A i C pravokutnika ABCD povućene su okomice AP i CQ na dijagonalu BD.Točke P i Q dijele dijagonalu DB na dijelove čije se duljine odnose kao 1:4:1.Ako je duljina dulje stranice pravokutnika 10cm,odredite njegovu površinu. |
Rečeno je točke 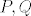 dijele dijagonalu dijele dijagonalu 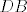 u omjeru u omjeru 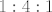 , pa možemo pisati: , pa možemo pisati: 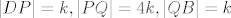 . .
Promotrimo pravokutni trokut 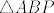 i napišimo relaciju Pitagorinog poučka za taj trokut: i napišimo relaciju Pitagorinog poučka za taj trokut:
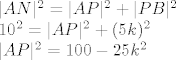
Promotrimo onda i pravokutni trokut 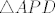 i napišimo za njega relaciju Pitagorinog poučka: i napišimo za njega relaciju Pitagorinog poučka:
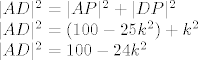
Raspišimo još relaciju Pitagorinog poučka za trokut 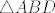 : :
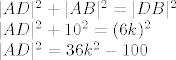
Vidimo da možemo pisati (jer je 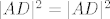 ): ):
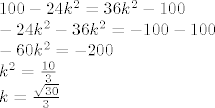
Vratimo se malo unazad gdje smo imali:
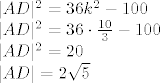
I odgovor...površina tog pravokutnika jednaka je 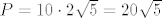
Added after 23 minutes:
| zada.4 (napisa): | Trokut ABC,s kutovima α=20,β=75,γ=85 upisana je kružnica sa središtem O. Neka je K točka na stranici AB takva da je |AK| |BK|=|CK|2 .Dokažite da je OK(okomito) CK.
Ako može netko neka rjesi. Hvala |
Pretpostavljam da je trokut upisan u kružnicu jer samo tako ima smisla... 
Dakle, jedino što mi pada na pamet jest koristiti potenciju točke na kružnici. U ovom slučaju potencije točke 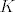 na danu kružnicu. na danu kružnicu.
Podsjetimo prije toga što je potencija kružnice... Neka je dana kružnica  i neka točka i neka točka  koja ne leži na kružnici. Iz točke koja ne leži na kružnici. Iz točke  povucimo pravac koji siječe kružnicu povucimo pravac koji siječe kružnicu  u dvije točke, u dvije točke, 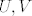 . Potencija točke . Potencija točke  na kružnicu na kružnicu  jest realni broj jest realni broj  . Štoviše vrijedi da taj broj ne ovisi o izboru pravca, već samo o izboru točke . Štoviše vrijedi da taj broj ne ovisi o izboru pravca, već samo o izboru točke  . .
E sad, u zadatku se kaže da je točka 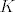 odabrana tako da vrijedi odabrana tako da vrijedi 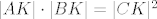 . Ovdje se zapravo radi o potenciji točke . Ovdje se zapravo radi o potenciji točke 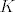 na kružnicu, ali preko dva različita pravca: preko pravca na kružnicu, ali preko dva različita pravca: preko pravca 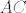 i preko pravca i preko pravca 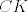 . .
Pogledajmo još i ovo:
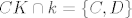
A iz relacije potencije točke na kružnicu imamo:
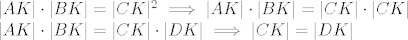
Odnosno, točke 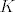 je polovište dužine je polovište dužine 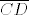 , a , a 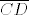 je tetiva zadane kružnice. je tetiva zadane kružnice.
I za kraj: znamo da ako promjer kružnice prolazi polovištem tetive, onda je on okomit na tetivu, odnosno - 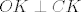 . .
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Anna Lee
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
keko
Forumaš(ica)
Pridružen/a: 23. 11. 2009. (14:30:24)
Postovi: (16)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pajson
Forumaš(ica)

Pridružen/a: 08. 05. 2006. (12:40:32)
Postovi: (57)16
Spol: 
Lokacija: ZAGREB
|
|
| [Vrh] |
|
keko
Forumaš(ica)
Pridružen/a: 23. 11. 2009. (14:30:24)
Postovi: (16)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
|











