| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:53 sub, 2. 1. 2010 Naslov: Postano: 18:53 sub, 2. 1. 2010 Naslov: |
    |
|
|
Imaš negdje nešto slično riješeno, Gino je riješio, stavio u pdf čak :D
A postupak je da uzmeš sve u matricu, ko da rješavaš običan sustav, samo imaš lambdu unutra. Dovedeš tu matricu na gornjetrokutast oblik i onda diskusija:
ako je zadnji redak 0*x_n=0 ,onda ima besk rješenja
ako je zadnji redak 0*x_n=nešto, onda nema rješenja
ako ne nešto*x_n=nešto2 onda ima jedinstveno rješenje
(x_n je zadnja nepoznanica, kad dovedeš u gornjetrokutast oblik samo ona ostane)
Imaš negdje nešto slično riješeno, Gino je riješio, stavio u pdf čak 
A postupak je da uzmeš sve u matricu, ko da rješavaš običan sustav, samo imaš lambdu unutra. Dovedeš tu matricu na gornjetrokutast oblik i onda diskusija:
ako je zadnji redak 0*x_n=0 ,onda ima besk rješenja
ako je zadnji redak 0*x_n=nešto, onda nema rješenja
ako ne nešto*x_n=nešto2 onda ima jedinstveno rješenje
(x_n je zadnja nepoznanica, kad dovedeš u gornjetrokutast oblik samo ona ostane)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:36 sub, 2. 1. 2010 Naslov: Postano: 19:36 sub, 2. 1. 2010 Naslov: |
    |
|
|
Možda ti pomogne da se diskusija javlja za [latex]\lambda=-19[/latex] (sustav nema rješenja), tj. [latex]\lambda \neq -19[/latex] (sustav ima jedinstveno rješenje).
Rješenje možeš provjeriti na [url=http://www.wolframalpha.com]Wolfram Alphi[/url]. Utipkaj sljedeće:
Solve[{x_1+x_2+x_3-x_4=1,x_1+2 x_2+2 x_3+x_4=2,3 x_2-x_3+7 x_4=-1,x_1+x_2+A x_3+4 x_4=2},{x_1,x_2,x_3,x_4}]
(promijenio sam [latex]\lambda[/latex] u A, nadam se da to nije problem :))
Možda ti pomogne da se diskusija javlja za 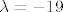 (sustav nema rješenja), tj. (sustav nema rješenja), tj. 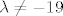 (sustav ima jedinstveno rješenje). (sustav ima jedinstveno rješenje).
Rješenje možeš provjeriti na Wolfram Alphi. Utipkaj sljedeće:
Solve[{x_1+x_2+x_3-x_4=1,x_1+2 x_2+2 x_3+x_4=2,3 x_2-x_3+7 x_4=-1,x_1+x_2+A x_3+4 x_4=2},{x_1,x_2,x_3,x_4}]
(promijenio sam  u A, nadam se da to nije problem u A, nadam se da to nije problem  ) )
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 11:19 ned, 3. 1. 2010 Naslov: Postano: 11:19 ned, 3. 1. 2010 Naslov: |
    |
|
|
ak sam skonto zadatak, imaš sam sustav četiri jednadžbe s četiri nepoznanice. razlika prvog i četvrtog stupca je vektor (0,-3,-3,0), to treba bit s desne strane. dobije se da je četvrta jednadžba 0 = 0, što nije baš od neke pomoći, i da prva i treća generiraju iste uvjete na nepoznanice pa se onda dobije parametarsko rješenje po dva parametra.
ak sam skonto zadatak, imaš sam sustav četiri jednadžbe s četiri nepoznanice. razlika prvog i četvrtog stupca je vektor (0,-3,-3,0), to treba bit s desne strane. dobije se da je četvrta jednadžba 0 = 0, što nije baš od neke pomoći, i da prva i treća generiraju iste uvjete na nepoznanice pa se onda dobije parametarsko rješenje po dva parametra.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:05 ned, 3. 1. 2010 Naslov: Postano: 15:05 ned, 3. 1. 2010 Naslov: |
    |
|
|
[quote=".anchy."]tako sam i ja prvo pomislila,ali me buni što se elementarnim transformacijama mijenja i razlika,tj. B[/quote]
Istina je da se B mijenja, ali ne bilo kako.
Neka je [latex]A'[/latex] matrica dobivena iz [latex]A[/latex] nekom elem. trans. nad recima, i [latex]B'[/latex] razlika 1. i 4. stupca od [latex]A'[/latex]. Primjeti da je [latex]B'[/latex] možeš dobiti iz [latex]B[/latex] primjenom iste elem. trans. (nad istim retkom, naravno). Dakle, [latex]B[/latex] će uvijek biti razlika 1. i 4. stupca od [latex]A[/latex] nakon kolko-god elem. trans. nad recima.
Poanta je da, kad bi rješavali sustav [latex]AX=B[/latex], zapisali bi ga u matricu [latex]\left[A|B\right][/latex], koju možemo (po gornjem argumentu) elem. trans. nad recima svesti na [latex]\left[\begin{array}{cccc|c}
1 & 2 & 0 & 1 & 0 \\
0 & 0 & 1 & 3 & -3 \\
1 & 2 & 1 & 4 & -3 \\
0 & 0 & 0 & 0 & 0 \end{array}\right][/latex]. Zato se rješenje svodi na ono što su Milojko i Grga rekli.
| .anchy. (napisa): | | tako sam i ja prvo pomislila,ali me buni što se elementarnim transformacijama mijenja i razlika,tj. B |
Istina je da se B mijenja, ali ne bilo kako.
Neka je 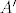 matrica dobivena iz matrica dobivena iz  nekom elem. trans. nad recima, i nekom elem. trans. nad recima, i 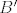 razlika 1. i 4. stupca od razlika 1. i 4. stupca od 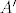 . Primjeti da je . Primjeti da je 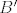 možeš dobiti iz možeš dobiti iz  primjenom iste elem. trans. (nad istim retkom, naravno). Dakle, primjenom iste elem. trans. (nad istim retkom, naravno). Dakle,  će uvijek biti razlika 1. i 4. stupca od će uvijek biti razlika 1. i 4. stupca od  nakon kolko-god elem. trans. nad recima. nakon kolko-god elem. trans. nad recima.
Poanta je da, kad bi rješavali sustav 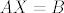 , zapisali bi ga u matricu , zapisali bi ga u matricu 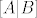 , koju možemo (po gornjem argumentu) elem. trans. nad recima svesti na , koju možemo (po gornjem argumentu) elem. trans. nad recima svesti na  . Zato se rješenje svodi na ono što su Milojko i Grga rekli. . Zato se rješenje svodi na ono što su Milojko i Grga rekli.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:05 pon, 4. 1. 2010 Naslov: Postano: 12:05 pon, 4. 1. 2010 Naslov: |
    |
|
|
[quote="Flame"]ipak bi trebalo i formalno dokazati da je to zaista tako[/quote]
Naravno, samo mi se nije dalo pisati, ali evo.
Možemo BSO promatrati prva dva retka s neki proizvoljnim članovima. To bi izgledalo ovako: [latex]
\left[\begin{array}{cccc|c}
a & ? & ? & b & a-b \\
c & ? & ? & d & c-d \\
? & ? & ? & ? & ? \\
? & ? & ? & ? & ?
\end{array}\right][/latex]
I sad, zamjena redaka očito štima, množenje (npr. prvog) retka nenul skalarom isto zbog distributivnosti množenja prema zbrajanju u polju realnih brojeva. Za kraj, pomnožimo prvi redak s [latex]\lambda[/latex] i dodamo u drugi i dobimo: [latex]
\left[\begin{array}{cccc|c}
a & ? & ? & b & a-b \\
\lambda a+c & ? & ? & \lambda b+d & \lambda(a-b)+c-d \\
? & ? & ? & ? & ? \\
? & ? & ? & ? & ?
\end{array}\right][/latex]. Ovo je isto kak spada i time smo gotovi. Zadnji stupac je doista uvijek razlika 1. i 4. stupca.
| Flame (napisa): | | ipak bi trebalo i formalno dokazati da je to zaista tako |
Naravno, samo mi se nije dalo pisati, ali evo.
Možemo BSO promatrati prva dva retka s neki proizvoljnim članovima. To bi izgledalo ovako: 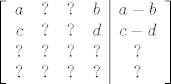
I sad, zamjena redaka očito štima, množenje (npr. prvog) retka nenul skalarom isto zbog distributivnosti množenja prema zbrajanju u polju realnih brojeva. Za kraj, pomnožimo prvi redak s  i dodamo u drugi i dobimo: i dodamo u drugi i dobimo: 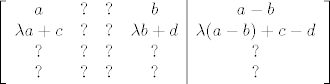 . Ovo je isto kak spada i time smo gotovi. Zadnji stupac je doista uvijek razlika 1. i 4. stupca. . Ovo je isto kak spada i time smo gotovi. Zadnji stupac je doista uvijek razlika 1. i 4. stupca.
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 0:59 sri, 6. 1. 2010 Naslov: Postano: 0:59 sri, 6. 1. 2010 Naslov: |
    |
|
|
pa mislim da se to traži
ne znam štab drugo moglo znači invertirat matricu
pa mislim da se to traži
ne znam štab drugo moglo znači invertirat matricu
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:32 ned, 17. 1. 2010 Naslov: Postano: 20:32 ned, 17. 1. 2010 Naslov: |
    |
|
|
Za takve stavri dobro dođe [url=http://www.wolframalpha.com/]Wolfram Alpha[/url]. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}].
Za takve stavri dobro dođe Wolfram Alpha. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}].
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
 Postano: 23:14 ned, 17. 1. 2010 Naslov: Postano: 23:14 ned, 17. 1. 2010 Naslov: |
    |
|
|
[quote="pmli"]Za takve stavri dobro dođe [url=http://www.wolframalpha.com/]Wolfram Alpha[/url]. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}].[/quote]
hvala :)
| pmli (napisa): | | Za takve stavri dobro dođe Wolfram Alpha. Utipkaj Inverse[{{2,1,2},{1,2,2},{3,3,3}}]. |
hvala 
|
|
| [Vrh] |
|
Altair
Forumaš(ica)

Pridružen/a: 08. 12. 2009. (14:26:52)
Postovi: (16)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:55 pon, 18. 1. 2010 Naslov: Postano: 23:55 pon, 18. 1. 2010 Naslov: |
    |
|
|
Što ako je [latex]\lambda=-2[/latex]?
Opet, provjeri u Wolfram Alphi (MatrixRank[{{1,4,3,-2},{2,2,1,7},{4,1,-2,4},{-1,5,6,1}}]). [size=4]Trebali bi mi platiti koliko reklamiram njihov proizvod[/size]
Što ako je 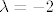 ? ?
Opet, provjeri u Wolfram Alphi (MatrixRank[{{1,4,3,-2},{2,2,1,7},{4,1,-2,4},{-1,5,6,1}}]). Trebali bi mi platiti koliko reklamiram njihov proizvod
|
|
| [Vrh] |
|
|

















