Drugi zadatak iz zadataka za vježbu [url]http://web.math.hr/nastava/difraf/zadaca2009.pdf[/url] što se tiče implicitno zadanih funkcija. U zadatku se traži da pokažemo da postoji funkcija [latex]f[/latex] t.d. zadovoljava nešto u čemu se traži [latex]f^3[/latex]. Mogu li ja reći da je [latex]g = f^3[/latex] i dokažem da postoji [latex]g[/latex] diferencijablina pa zaključim da postoji i [latex]f[/latex] diferencijabilna.
Ako ne mogu, zašto ne mogu?
I, kada bi to rješavao bez te supstitucije, dobio bi
[latex]3w^2(1+e^{-(\cdots)})[/latex] što predstavlja determinantu iz uvjeta koja mora biti veća od 0. Međutim ova može biti i 0 kada je w = 0. Što da tu napravim?
Hvala
Drugi zadatak iz zadataka za vježbu http://web.math.hr/nastava/difraf/zadaca2009.pdf što se tiče implicitno zadanih funkcija. U zadatku se traži da pokažemo da postoji funkcija 
t.d. zadovoljava nešto u čemu se traži 
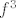. Mogu li ja reći da je 
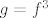i dokažem da postoji 
diferencijablina pa zaključim da postoji i diferencijabilna.
Ako ne mogu, zašto ne mogu?
I, kada bi to rješavao bez te supstitucije, dobio bi
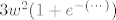što predstavlja determinantu iz uvjeta koja mora biti veća od 0. Međutim ova može biti i 0 kada je w = 0. Što da tu napravim?
Hvala
_________________
reductio ad absurdum
