| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 13:12 čet, 7. 1. 2010 Naslov: dekompozicija Postano: 13:12 čet, 7. 1. 2010 Naslov: dekompozicija |
    |
|
|
Neka imamo matricu [latex]\Theta\in M_N(\mathbb{R})[/latex], i oznacimo realne svojstvene vrijednosti sa [latex](\lambda_1,\dots,\lambda_K)[/latex], te preostale sa [latex](\gamma_1\pm i\omega_1),\dots,(\gamma_J\pm i\omega_J),~K+2J=N[/latex]. Neka je [latex]B\in M_N(\mathbb{C})[/latex], sacinjena od svojstvenih vektora matrice [latex]\Theta[/latex] (ti vektori dakako mogu biti iz [latex]\mathbb{C}^N[/latex]). Definiramo novu matricu [latex]A=Re(B)-Im(B)[/latex].
Tvrdi se da je [latex]\Theta=A\Gamma A^{-1}[/latex], gdje je [latex]\Gamma[/latex], blok-dijagonalna matrica [latex]\Gamma=diag\{\lambda_1,\dots,\lambda_K,\Gamma_1,\dots,\Gamma_J\}[/latex], gdje je [latex]\Gamma_j=\begin{pmatrix} \gamma_j & \omega_j \\ -\omega_j & \gamma_j \end{pmatrix} ~,j=1,\dots,J[/latex].
No, lagano ja provjerim da je doista tako (tj. da se doista dekompozicija moze napraviti na takav nacin), no nije mi jasno od kuda to..? Lici na spektralni teorem, no nisam siguran da bi mogao izvesti ovakvu dekompoziciju.
Svaka pomoc je dobrodosla :D .
Edit: malo sam zeznuo oznake...sada je dobro.
Neka imamo matricu 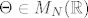 , i oznacimo realne svojstvene vrijednosti sa , i oznacimo realne svojstvene vrijednosti sa 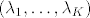 , te preostale sa , te preostale sa 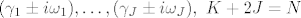 . Neka je . Neka je 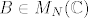 , sacinjena od svojstvenih vektora matrice , sacinjena od svojstvenih vektora matrice 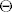 (ti vektori dakako mogu biti iz (ti vektori dakako mogu biti iz 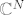 ). Definiramo novu matricu ). Definiramo novu matricu 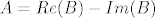 . .
Tvrdi se da je 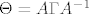 , gdje je , gdje je 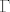 , blok-dijagonalna matrica , blok-dijagonalna matrica 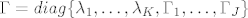 , gdje je , gdje je 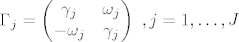 . .
No, lagano ja provjerim da je doista tako (tj. da se doista dekompozicija moze napraviti na takav nacin), no nije mi jasno od kuda to..? Lici na spektralni teorem, no nisam siguran da bi mogao izvesti ovakvu dekompoziciju.
Svaka pomoc je dobrodosla  . .
Edit: malo sam zeznuo oznake...sada je dobro.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:09 čet, 7. 1. 2010 Naslov: Postano: 19:09 čet, 7. 1. 2010 Naslov: |
    |
|
|
Sličan teorem je teroem o realnoj schurovoj formi, dokaz možeš naći [url=http://www.fsb.hr/mat-4/PA2/eig_val.pdf]tu[/url]. On kaže da se svaka realna matrica može ortogonalnom sličnošću dovesti do blok gornje trokutaste, s time da su na dijagonali 1x1 blokovi koji su realne sv vrijednosti, ili 2x2 blokovi, kojima su svojstvene vrijednosti komplexno konjugirani parovi sv vrijednosti početne matrice.
Kod tebe bi rekao da se dalje može iz te trokutaste doć do dijagonalne, ali tu više ne može ortogonalna sličnost, nego "obična". Na kraju bi samo trebalo pokazati da je ta matrica s kojom se radi sličnost upravo ova koja je dana teoremom :D
edit:
kod tebe sigurno vrijedi da se theta može prikazati kao [latex]\Theta=B\cdot \Lambda \cdot B^*[/latex], a inače svojstveni vektori koji su pridruženi komplexnim sv vrijednostima su nužno komplexni jer je Theta realna matrica. (ovdje je Lambda dijagonalna sa sv vrijednostima na dijagonali)
Ako sam nešto zeznuo u zaključivanje nek netko viče :D Ovaj edit nisam dokazivo, ali mislim da bi išlo to tako :D
Sličan teorem je teroem o realnoj schurovoj formi, dokaz možeš naći tu. On kaže da se svaka realna matrica može ortogonalnom sličnošću dovesti do blok gornje trokutaste, s time da su na dijagonali 1x1 blokovi koji su realne sv vrijednosti, ili 2x2 blokovi, kojima su svojstvene vrijednosti komplexno konjugirani parovi sv vrijednosti početne matrice.
Kod tebe bi rekao da se dalje može iz te trokutaste doć do dijagonalne, ali tu više ne može ortogonalna sličnost, nego "obična". Na kraju bi samo trebalo pokazati da je ta matrica s kojom se radi sličnost upravo ova koja je dana teoremom 
edit:
kod tebe sigurno vrijedi da se theta može prikazati kao 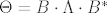 , a inače svojstveni vektori koji su pridruženi komplexnim sv vrijednostima su nužno komplexni jer je Theta realna matrica. (ovdje je Lambda dijagonalna sa sv vrijednostima na dijagonali) , a inače svojstveni vektori koji su pridruženi komplexnim sv vrijednostima su nužno komplexni jer je Theta realna matrica. (ovdje je Lambda dijagonalna sa sv vrijednostima na dijagonali)
Ako sam nešto zeznuo u zaključivanje nek netko viče  Ovaj edit nisam dokazivo, ali mislim da bi išlo to tako Ovaj edit nisam dokazivo, ali mislim da bi išlo to tako 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 20:09 čet, 7. 1. 2010 Naslov: Postano: 20:09 čet, 7. 1. 2010 Naslov: |
    |
|
|
Bacio sam pogled na file dan u linku...dokaz donekle odgovara ovome sta ja zelim, no problem vidim u sljedecem; oni doista grade "slicnosti" preko svojstvenih vektora, i pretpostavimo da smo dosli do tih matrica ([latex]\Theta=V \widehat{\Gamma} V^{\tau}[/latex]), ali onda bi nekako trebalo zakljuciti da se mi mozemo rijesiti svega iznad (blok-)dijagonale, neka je to onda jos jedna meta-dekompozicija gornje-trokutaste matrice sa blokovima na dijagonali ([latex]\widehat{\Gamma}=S\Gamma S^{-1}[/latex]), no onda bi trebalo pokazati da tada matrica [latex]VS[/latex] je realna(!!), te da odgovara matrici [latex]A[/latex].
Moram priznati da uopce nisam uvjeren... :?. Ali budem probao, za sada mi nije ocito.
Naravno, lagano je moguce da dekompozicija o kojoj govorim uopce ne postoji :roll: (ali tako pise u clanku, pa valjda covjek zna sta pise).
Edit: mene zapravo najvise muci, sto je matricu [latex]A[/latex] izvukao iz sesira...uopce ne vidim odakle to, i zasto.
Bacio sam pogled na file dan u linku...dokaz donekle odgovara ovome sta ja zelim, no problem vidim u sljedecem; oni doista grade "slicnosti" preko svojstvenih vektora, i pretpostavimo da smo dosli do tih matrica (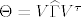 ), ali onda bi nekako trebalo zakljuciti da se mi mozemo rijesiti svega iznad (blok-)dijagonale, neka je to onda jos jedna meta-dekompozicija gornje-trokutaste matrice sa blokovima na dijagonali ( ), ali onda bi nekako trebalo zakljuciti da se mi mozemo rijesiti svega iznad (blok-)dijagonale, neka je to onda jos jedna meta-dekompozicija gornje-trokutaste matrice sa blokovima na dijagonali (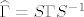 ), no onda bi trebalo pokazati da tada matrica ), no onda bi trebalo pokazati da tada matrica 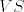 je realna(!!), te da odgovara matrici je realna(!!), te da odgovara matrici  . .
Moram priznati da uopce nisam uvjeren...  . Ali budem probao, za sada mi nije ocito. . Ali budem probao, za sada mi nije ocito.
Naravno, lagano je moguce da dekompozicija o kojoj govorim uopce ne postoji  (ali tako pise u clanku, pa valjda covjek zna sta pise). (ali tako pise u clanku, pa valjda covjek zna sta pise).
Edit: mene zapravo najvise muci, sto je matricu  izvukao iz sesira...uopce ne vidim odakle to, i zasto. izvukao iz sesira...uopce ne vidim odakle to, i zasto.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:45 čet, 7. 1. 2010 Naslov: Postano: 20:45 čet, 7. 1. 2010 Naslov: |
    |
|
|
Ajmo ovako, kako mene intuicija vodi... kad imamo običnu gornje trokutastu matricu A (dakle ne blok trokutastu), onda svakako možemo doći do dijagonalne sa nekom regularnom matricom. Naprosto radimo elementarne transformacije redaka od zadnjeg prema prvom, i to tako da po redu poništavamo. Sa [latex]A_{n,n}[/latex] poništimo cijeli zadnji stupac, pa sa [latex]A_{n-1,n-1}[/latex] poništimo cijeli n-1-vi stupac itd. Tako dobijemo dijagonalnu. Ako je neki od elemenata nula, onda možemo do blok dijagonalne.
E sad, kod blok trokutaste bi išla ista fora za ove realne dijelove (npr da njih stavimo skroz dolje, to možemo sa matricom permutacije). U jednom trenu dođemo do onih blokova. Ti blokovi su svi regularni (jer im nula nije sv vrijednost, ona je eventualno u ovim realnim blokovima), pa imaju inverz. Dakle, one blok matrice koje se dalje pojavljuju u trokutastom dijelu možemo poništit ( Ako je matrica T koju trebamo poništit, a imamo Ak, onda to napravimo tako da redak sa Ak pomnožimo sa -Ak^-1*T i dodamo retku sa T.) Tu će jasno i matrica di ćemo čuvat te transformacije opet bit blokovske strukture.
To je moja intuicija, a sad kak to izvest i lijepo napisat, i dal je to uopće ok, to je drugo pitanje... i ak uspiješ, dal je to jednako onoj matrici A u teoremu, to je pak još jedno pitanje... ali možda ti da neku ideju. :D
Btw možda da pitaš prof Drmača, on je dosta jak u matričnoj teoriji... sutra ima konzultacije od 11 ja mislim.
Ajmo ovako, kako mene intuicija vodi... kad imamo običnu gornje trokutastu matricu A (dakle ne blok trokutastu), onda svakako možemo doći do dijagonalne sa nekom regularnom matricom. Naprosto radimo elementarne transformacije redaka od zadnjeg prema prvom, i to tako da po redu poništavamo. Sa 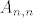 poništimo cijeli zadnji stupac, pa sa poništimo cijeli zadnji stupac, pa sa 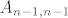 poništimo cijeli n-1-vi stupac itd. Tako dobijemo dijagonalnu. Ako je neki od elemenata nula, onda možemo do blok dijagonalne. poništimo cijeli n-1-vi stupac itd. Tako dobijemo dijagonalnu. Ako je neki od elemenata nula, onda možemo do blok dijagonalne.
E sad, kod blok trokutaste bi išla ista fora za ove realne dijelove (npr da njih stavimo skroz dolje, to možemo sa matricom permutacije). U jednom trenu dođemo do onih blokova. Ti blokovi su svi regularni (jer im nula nije sv vrijednost, ona je eventualno u ovim realnim blokovima), pa imaju inverz. Dakle, one blok matrice koje se dalje pojavljuju u trokutastom dijelu možemo poništit ( Ako je matrica T koju trebamo poništit, a imamo Ak, onda to napravimo tako da redak sa Ak pomnožimo sa -Ak^-1*T i dodamo retku sa T.) Tu će jasno i matrica di ćemo čuvat te transformacije opet bit blokovske strukture.
To je moja intuicija, a sad kak to izvest i lijepo napisat, i dal je to uopće ok, to je drugo pitanje... i ak uspiješ, dal je to jednako onoj matrici A u teoremu, to je pak još jedno pitanje... ali možda ti da neku ideju. 
Btw možda da pitaš prof Drmača, on je dosta jak u matričnoj teoriji... sutra ima konzultacije od 11 ja mislim.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|






