|
Nekolicini ljudi sam obećao da ću napisati na forumu, pa evo da održim obećanje, nadam se da će pomoći! :)
[b]Propozicija 12.14.[/b]
Neka je [latex]A \subseteq \mathbb{R}^n[/latex] otvoren.
Neka su funkcije [latex]f : A \to \mathbb{R}^m[/latex], [latex]g : A \to \mathbb{R}[/latex] diferencijabilne u točki [latex]c \in A[/latex].
Tada je [latex]gf : A \to \mathbb{R}^m[/latex] također diferencijabilna u točki [latex]c[/latex] te vrijedi
[latex]\mathrm{D}\left(gf\right)\left(c\right)v=g\left(c\right)\mathrm{D}f\left(c\right)v + \left(\mathrm{D}g\left(c\right)v\right)f\left(c\right),\ \forall v \in \mathbb{R}^n[/latex].
[b]Dokaz.[/b] Sami. :D
Šalim se, dakle, želimo dokazati da je
[latex]\lim\limits_{x \to c}\frac{\left\|\left(gf\right)\left(x\right)-\left(gf\right)\left(c\right)-g\left(c\right)\mathrm{D}f\left(c\right)\left(x-c\right) - \left[\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)\right\|}{\left\|x-c\right\|}=0. \qquad (*)[/latex]
Sada ćemo se malo igrati naštimavanja (ili kako bi moj profesor iz srednje rekao, dodati ćemo ono što nam nedostaje do potpune sreće :D).
Naime, idemo u tom smjeru da dođemo u situaciju u kojoj možemo iskoristiti svojstvo diferencijabilnosti funkcija [latex]f[/latex] i [latex]g[/latex] u točki [latex]c[/latex],
također nam je bitno da je funkcija lokalno Lipschitzova u točki u kojoj je diferencijabilna.
Vrijedi
[latex]\left(gf\right)\left(x\right)-\left(gf\right)\left(c\right)-g\left(c\right)\mathrm{D}f\left(c\right)\left(x-c\right) - \left[\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)=[/latex]
[latex]g\left(x\right)f\left(x\right) - \underline{g\left(c\right)f\left(c\right)} - \underline{g\left(c\right)\mathrm{D}f\left(c\right)\left(x-c\right)}-\left[\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)=[/latex]
[latex]\left[\right.[/latex]Nadodajemo ono što nam nedostaje do potpune sreće: [latex]\left.+g\left(c\right)f\left(x\right)-g\left(c\right)f\left(x\right)\right][/latex]
[latex]g\left(c\right)\left[f\left(x\right)-f\left(c\right)-\mathrm{D}f\left(c\right)\left(x-c\right)\right] + g\left(x\right)f\left(x\right) - g\left(c\right)f\left(x\right)-\underline{\left[\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)}=[/latex]
[latex]\left[+g\left(x\right)f\left(c\right)-g\left(c\right)f\left(c\right)-g\left(x\right)f\left(c\right)+g\left(c\right)f\left(c\right)\right][/latex]
[latex]g\left(c\right)\left[f\left(x\right)-f\left(c\right)-\mathrm{D}f\left(c\right)\left(x-c\right)\right]+\left[g\left(x\right)-g\left(c\right)-\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)+[/latex]
[latex]+\underline{g\left(x\right)f\left(x\right)-g\left(x\right)f\left(c\right)}-\underline{g\left(c\right)f\left(x\right)+g\left(c\right)f\left(c\right)}=[/latex]
[latex]g\left(c\right)\left[\underline{f\left(x\right)-f\left(c\right)-\mathrm{D}f\left(c\right)\left(x-c\right)}\right]+\left[\underline{g\left(x\right)-g\left(c\right)-\mathrm{D}g\left(c\right)\left(x-c\right)}\right]f\left(c\right)+\left[\underline{g\left(x\right)-g\left(c\right)}\right]\left[\underline{f\left(x\right)-f\left(c\right)}\right][/latex].
Sada po nejednakosti trokuta imamo
[latex]\frac{\left\|\left(gf\right)\left(x\right)-\left(gf\right)\left(c\right)-g\left(c\right)\mathrm{D}f\left(c\right)\left(x-c\right) - \left[\mathrm{D}g\left(c\right)\left(x-c\right)\right]f\left(c\right)\right\|}{\left\|x-c\right\|} \leq[/latex]
[latex]\leq |g\left(c\right)|\frac{\left\|f\left(x\right)-f\left(c\right)-\mathrm{D}f\left(c\right)\left(x-c\right)\right\|}{\left\|x-c\right\|} + \frac{\left\|g\left(x\right)-g\left(c\right)-\mathrm{D}g\left(c\right)\left(x-c\right)\right\|}{\left\|x-c\right\|}\left\|f\left(c\right)\right\| + \frac{\left\|g\left(x\right)-g\left(c\right)\right\| \cdot \left\|f\left(x\right)-f\left(c\right)\right\|}{\left\|x-c\right\|}. \qquad (**)[/latex]
Jasno je da prva dva člana na desnoj strani dobivene nejednakosti idu u [latex]0[/latex] kada [latex]x \to c[/latex].
Naime, to direktno slijedi iz diferencijabilnosti funkcija [latex]f[/latex] i [latex]g[/latex] u točki [latex]c[/latex]
te činjenice da je [latex]g\left(c\right)[/latex] neki čvrsti realni broj, te [latex]f\left(c\right)[/latex] neki čvrsti vektor iz [latex]\mathbb{R}^m[/latex].
Pošto su funkcije [latex]f[/latex] i [latex]g[/latex] diferencijabilne u točki [latex]c[/latex] slijedi da su one i Lokalno Lipschitzove u točki [latex]c[/latex].
Dakle, postoje [latex]\delta_1>0,\, \delta_2>0,\, M_1>0,\, M_2>0[/latex] takvi da
[latex]\forall x \in A,\ \left\|x-c\right\| < \min\left\{\delta_1,\, \delta_2\right\} \Longrightarrow \left\|g\left(x\right)-g\left(c\right)\right\|\leq M_1\left\|x-c\right\|[/latex] i [latex]\left\|f\left(x\right)-f\left(c\right)\right\|\leq M_2\left\|x-c\right\|[/latex].
Iz ovoga je jasno da [latex]\forall x \in A,\ \left\|x-c\right\|< \min\left\{\delta_1,\, \delta_2\right\}[/latex] vrijedi da je
[latex]\frac{\left\|g\left(x\right)-g\left(c\right)\right\| \cdot \left\|f\left(x\right)-f\left(c\right)\right\|}{\left\|x-c\right\|} \leq M_1M_2\left\|x-c\right\|[/latex].
Ovime je pokazano da i treći član s desne strane nejednakosti [latex](**)[/latex] ide u [latex]0[/latex] kada [latex]x \to c[/latex]. Dakle, jednakost [latex](*)[/latex] je točna.
Propozicija konačno dokazana! :D
Eto, nadam se da je jasno i da nema greški. :)
Sretno svima! :)
Nekolicini ljudi sam obećao da ću napisati na forumu, pa evo da održim obećanje, nadam se da će pomoći! 
Propozicija 12.14.
Neka je 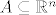 otvoren. otvoren.
Neka su funkcije 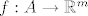 , , 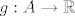 diferencijabilne u točki diferencijabilne u točki 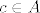 . .
Tada je 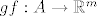 također diferencijabilna u točki također diferencijabilna u točki  te vrijedi te vrijedi
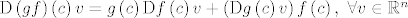 . .
Dokaz. Sami. 
Šalim se, dakle, želimo dokazati da je
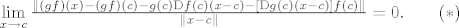
Sada ćemo se malo igrati naštimavanja (ili kako bi moj profesor iz srednje rekao, dodati ćemo ono što nam nedostaje do potpune sreće  ). ).
Naime, idemo u tom smjeru da dođemo u situaciju u kojoj možemo iskoristiti svojstvo diferencijabilnosti funkcija  i i  u točki u točki  , ,
također nam je bitno da je funkcija lokalno Lipschitzova u točki u kojoj je diferencijabilna.
Vrijedi
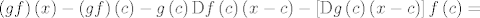
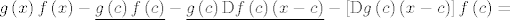
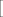 Nadodajemo ono što nam nedostaje do potpune sreće: Nadodajemo ono što nam nedostaje do potpune sreće: 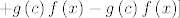
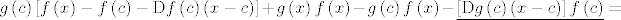
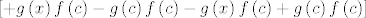
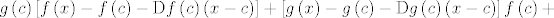

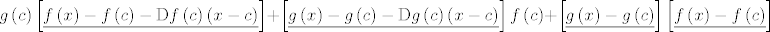 . .
Sada po nejednakosti trokuta imamo
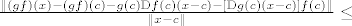
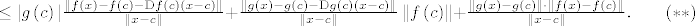
Jasno je da prva dva člana na desnoj strani dobivene nejednakosti idu u  kada kada  . .
Naime, to direktno slijedi iz diferencijabilnosti funkcija  i i  u točki u točki 
te činjenice da je 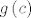 neki čvrsti realni broj, te neki čvrsti realni broj, te 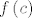 neki čvrsti vektor iz neki čvrsti vektor iz 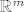 . .
Pošto su funkcije  i i  diferencijabilne u točki diferencijabilne u točki  slijedi da su one i Lokalno Lipschitzove u točki slijedi da su one i Lokalno Lipschitzove u točki  . .
Dakle, postoje 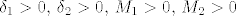 takvi da takvi da
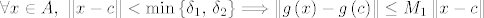 i i  . .
Iz ovoga je jasno da 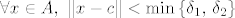 vrijedi da je vrijedi da je
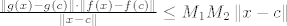 . .
Ovime je pokazano da i treći član s desne strane nejednakosti  ide u ide u  kada kada  . Dakle, jednakost . Dakle, jednakost  je točna. je točna.
Propozicija konačno dokazana! 
Eto, nadam se da je jasno i da nema greški. 
Sretno svima! 
|





