| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Perosito
Forumaš(ica)

Pridružen/a: 30. 01. 2004. (22:21:16)
Postovi: (7E)16
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 19:45 ned, 15. 2. 2004 Naslov: Re: Pitanja s usmenog Postano: 19:45 ned, 15. 2. 2004 Naslov: Re: Pitanja s usmenog |
    |
|
|
[quote="Perosito"]Ovako, tražim tu na forumu, al niko nije stavil još nikakva pitanja koja su se pojavljivala na usmenom kod prof. Nogo, pa s namjerom da pomognemo svima koji će izaći na usmeni proglašavam ovaj post otvorenim! 8) Vjerujem da ima dobrih duša koji nam žele pomoći![/quote]
pisat cu po redu jer mi ih se neda grupirati :g:
i bez rjesenja
[list=1]
[*]dokazati (n povrh r)*(r povrh k) = (n povrh k)*(n-k povrh r-k) kombinatorno
[*]dokazati rekurziju S(n,k)=S(n-1,k-1) + k*S(n-1,k)
dokazat da je suma (po k = 0 do n) S(n,k)*x^k_ = x^n [i]k_ je k dolje potez - padajuci faktorijel, broj injekcija[/i] kombinatorno
koliko je S(n,0)
[*] sto je skup rjesenja homogene rekurzije
[*]poopceni FUI [i]ono sa f(T)=suma (po X podskup T) (-1)^|T-X|*g(X), nesto o tome, sto su operatori fi i psi u pocetku dokaza i kako otprilike dokaz ide[/i]
[*]izvesti rekurziju za broj binarnih stabala
[*]FjaIz za Catalanove brojeve [i]covjek je isao preko prethodne rekurzije, no prof je predlozila da proba i simbolickom metodom[/i]
[*]definirati r kombinacije s ponavljanjem
dokazati koliko je to
[*]dokazati (n povrh r) = (n povrh n-r)
[*]dokazati suma (po k=0 do n) (n povrh k)^2 = (2n povrh n)
[*]Stirlingovi brojevi prve vrste [i]sto su i koja im je formula[/i]
[*]dokazati rekurziju c(n,k)=c(n-1, k-1) + (n-1)*c(n-1,k) kombinatorno
[*]dokazati suma (po k=0 do n) c(n,k)*x^k = x^n~ [i]gdje je n~ n gore potez, rastuci faktorijel[/i]
[*]FUI tm, iskaz i dokaz kombinatorno
[*]lijevi pomak kod FjaIz sto je
[*]sto je binomna konvolucija i napisati
[*]rekurzija za broj deranzmana, dokaz
[*]dokazati suma (k=0 do n) (n povrh k) = 2^n
[*]kakav je niz binomnih koeficijenata, opisati
[*]formula za n-ti Catalanov broj, veza s triangulacijom n-terokuta
[*]sto je eulerova fja
dokaz preko FUI
kakva je [i]mulitiplikativna za kakve brojeve[/i]
[*]topovski polinom
formula
sto je t_k
malo objasniti sto je sto u formuli
[*]parcijalna suma FjaIz
[*]osnovna rekurzija za quick sort
sto je sto u formuli, koje je rjesenje, kojeg je oblika FjaIz
[*]prosirenje binomne formule (Van der Mondeova konvolucija)
dokaz kombinatorno
[*]Stirlingovi brojevi druge vrste
formula
kako dobiti broj bijekcija
a broj surjekcija [i]u smislu sto treba uvrstiti, ili tako nekako[/i]
[*]dokazati FUI algebarski, preko karakteristicne fje
[*]broj surjekcija n-clanog na k-clani skup [i]formula #Sur(n,k)=... pomocu FUI[/i]
[*]sto je P(n) [i]broj particija od n[/i]
sto je FjaIz, i za koji niz
[*]sto je skaliranje FjeIz
[*]dokazati suma (k=0 do n-r)(r+k povrh k) = (n+1 povrh r+1)
dokazati suma (k=0 do r) (n+k povrh k) = (n + r +1 povrh r)
[*]koliki je broj permutacija multiskupa
[*]formula za binomni red
prosirenje (a povrh n) = ?
[*]dokazati suma (k=0 do min{m,n}) (m povrh k)*(n povrh k) = (m + n povrh n)
[*]simbolickom metodom dokazati svojstvo c) FjaIz [i]1/(1-A(x)) je FjaIz koja prebrojava sve nizove objekata iz lijepoA[/i]
[*]zadnji tm (o racionalnim FjamaIz) dokazati da je V_1 vektorski prostor
[*]lin. homog. rekurzija r-tog reda s konst. koef.
sto je skup rjesenja, dokazati
[*]propozicija o baznim rjesenjima[i]formula opceg rjesenja preko baznih[/i]
determinanta sustava koji se pojavi u dokazu, kolika je [i]VDM det, onaj umnozak[/i]
[*]dokazat pascalovu formulu kombinatorno [i](n povrh r) = (n-1 povrh r-1) * (n-1 povrh r)[/i]
[*]FUI dokazat indukcijom [i]zanimao ju je samo korak[/i]
[*]sto je graf permutacije
[*]sto je broj deranzmana
zapisati preko ploce
[*]dokazati iz zadnjeg TMa da je V_1=V_2=V_4
[*]koliko je suma (k=0 do n) (n povrh k) D_(n-k)
sto je D_(n-k)
[*]problem bracnih parova
opisati, rijesiti
[*]poopcena FUI, dokazati korolar
f=(k) = suma... f>=(k)=suma.... ( http://degiorgi.math.hr/forum/viewtopic.php?t=1372 ) cekamo dokaz :o)
sto je f=(T), f>=(T)
[*]veza izmedju c(n,k) i harmonijskih brojeva [i]c(n+1,2)=n!H_n[/i]
[*]koliko postoji uredjenih k-torki sa svojstvom 1<=x_1<x_2<...<x_k<=n
koliko je (2n)!!
a (2n-1)!!
[*]teorem o uzastopnom prebrojavanju [i]x_i element S_i, |S_i|=p_i za i=1 do k
k-torku (x_1,...,x_n) mozemo odabrati na p_1*p_2*...*p_k nacina[/i]
[*]broj permutacija ciklickog tipa, dokazat formulu
[*]sto je c(n,k)
koliko je c(n,n), c(n,0), c(0,0)
koliko je suma (k=0 do n) c(n,k)
[*]karakteristicni polinom lin. hom. rekurzije s konst. koef
sto je opce rjesenje ako korjeni nisu rezliciti
[*]Exponencijalne FjeIz
formula
e^x*A(x) je EFI kojeg niza (A(x) <-EFI-> E(x) )
[*]veza Catalanovih brojeva i puteva u cjelobrojnoj mrezi
formula za n-ti Catalanov broj
rekurzija za Catalanove brojeve
[*]algebarski dokaz FUI
ovo nisam bila osobno prisutna
[*]dokazati binomnu formulu indukcijom
[*]dokazati svojstvo apsorpcije binomnih koeficijenata [i]r* (n povrh r) = n* (n-1 povrh r-1)[/i]
[*]zadnji tm (o rac. FjamaIz) osnovna svojstva rac FjaIz
[/list:o]
to su sva pitanja
zbilja mi se neda pisati odgovore
no, ako nije nesto jasno (sto se trazi, ili koje je rjesenje - ono, kopate po biljeskama i udzbeniku i nemrete nac :) ), mogu pogledati u biljeskama s usmenog i probati pronaci (nisu bas sva pitanja odgovorena...)
ako ima greska, pitajte, moglo je doci do tipfelera (kojima sam ja po difoltu skolna :g:)
| Perosito (napisa): | Ovako, tražim tu na forumu, al niko nije stavil još nikakva pitanja koja su se pojavljivala na usmenom kod prof. Nogo, pa s namjerom da pomognemo svima koji će izaći na usmeni proglašavam ovaj post otvorenim!  Vjerujem da ima dobrih duša koji nam žele pomoći! Vjerujem da ima dobrih duša koji nam žele pomoći! |
pisat cu po redu jer mi ih se neda grupirati 
i bez rjesenja
- dokazati (n povrh r)*(r povrh k) = (n povrh k)*(n-k povrh r-k) kombinatorno
- dokazati rekurziju S(n,k)=S(n-1,k-1) + k*S(n-1,k)
dokazat da je suma (po k = 0 do n) S(n,k)*x^k_ = x^n k_ je k dolje potez - padajuci faktorijel, broj injekcija kombinatorno
koliko je S(n,0)
- sto je skup rjesenja homogene rekurzije
- poopceni FUI ono sa f(T)=suma (po X podskup T) (-1)^|T-X|*g(X), nesto o tome, sto su operatori fi i psi u pocetku dokaza i kako otprilike dokaz ide
- izvesti rekurziju za broj binarnih stabala
- FjaIz za Catalanove brojeve covjek je isao preko prethodne rekurzije, no prof je predlozila da proba i simbolickom metodom
- definirati r kombinacije s ponavljanjem
dokazati koliko je to
- dokazati (n povrh r) = (n povrh n-r)
- dokazati suma (po k=0 do n) (n povrh k)^2 = (2n povrh n)
- Stirlingovi brojevi prve vrste sto su i koja im je formula
- dokazati rekurziju c(n,k)=c(n-1, k-1) + (n-1)*c(n-1,k) kombinatorno
- dokazati suma (po k=0 do n) c(n,k)*x^k = x^n~ gdje je n~ n gore potez, rastuci faktorijel
- FUI tm, iskaz i dokaz kombinatorno
- lijevi pomak kod FjaIz sto je
- sto je binomna konvolucija i napisati
- rekurzija za broj deranzmana, dokaz
- dokazati suma (k=0 do n) (n povrh k) = 2^n
- kakav je niz binomnih koeficijenata, opisati
- formula za n-ti Catalanov broj, veza s triangulacijom n-terokuta
- sto je eulerova fja
dokaz preko FUI
kakva je mulitiplikativna za kakve brojeve
- topovski polinom
formula
sto je t_k
malo objasniti sto je sto u formuli
- parcijalna suma FjaIz
- osnovna rekurzija za quick sort
sto je sto u formuli, koje je rjesenje, kojeg je oblika FjaIz
- prosirenje binomne formule (Van der Mondeova konvolucija)
dokaz kombinatorno
- Stirlingovi brojevi druge vrste
formula
kako dobiti broj bijekcija
a broj surjekcija u smislu sto treba uvrstiti, ili tako nekako
- dokazati FUI algebarski, preko karakteristicne fje
- broj surjekcija n-clanog na k-clani skup formula #Sur(n,k)=... pomocu FUI
- sto je P(n) broj particija od n
sto je FjaIz, i za koji niz
- sto je skaliranje FjeIz
- dokazati suma (k=0 do n-r)(r+k povrh k) = (n+1 povrh r+1)
dokazati suma (k=0 do r) (n+k povrh k) = (n + r +1 povrh r)
- koliki je broj permutacija multiskupa
- formula za binomni red
prosirenje (a povrh n) = ?
- dokazati suma (k=0 do min{m,n}) (m povrh k)*(n povrh k) = (m + n povrh n)
- simbolickom metodom dokazati svojstvo c) FjaIz 1/(1-A(x)) je FjaIz koja prebrojava sve nizove objekata iz lijepoA
- zadnji tm (o racionalnim FjamaIz) dokazati da je V_1 vektorski prostor
- lin. homog. rekurzija r-tog reda s konst. koef.
sto je skup rjesenja, dokazati
- propozicija o baznim rjesenjimaformula opceg rjesenja preko baznih
determinanta sustava koji se pojavi u dokazu, kolika je VDM det, onaj umnozak
- dokazat pascalovu formulu kombinatorno (n povrh r) = (n-1 povrh r-1) * (n-1 povrh r)
- FUI dokazat indukcijom zanimao ju je samo korak
- sto je graf permutacije
- sto je broj deranzmana
zapisati preko ploce
- dokazati iz zadnjeg TMa da je V_1=V_2=V_4
- koliko je suma (k=0 do n) (n povrh k) D_(n-k)
sto je D_(n-k)
- problem bracnih parova
opisati, rijesiti
- poopcena FUI, dokazati korolar
f=(k) = suma... f>=(k)=suma.... ( http://degiorgi.math.hr/forum/viewtopic.php?t=1372 ) cekamo dokaz 
sto je f=(T), f>=(T)
- veza izmedju c(n,k) i harmonijskih brojeva c(n+1,2)=n!H_n
- koliko postoji uredjenih k-torki sa svojstvom 1⇐x_1<x_2<...<x_k⇐n
koliko je (2n)!!
a (2n-1)!!
- teorem o uzastopnom prebrojavanju x_i element S_i, |S_i|=p_i za i=1 do k
k-torku (x_1,...,x_n) mozemo odabrati na p_1*p_2*...*p_k nacina
- broj permutacija ciklickog tipa, dokazat formulu
- sto je c(n,k)
koliko je c(n,n), c(n,0), c(0,0)
koliko je suma (k=0 do n) c(n,k)
- karakteristicni polinom lin. hom. rekurzije s konst. koef
sto je opce rjesenje ako korjeni nisu rezliciti
- Exponencijalne FjeIz
formula
e^x*A(x) je EFI kojeg niza (A(x) ←EFI→ E(x) )
- veza Catalanovih brojeva i puteva u cjelobrojnoj mrezi
formula za n-ti Catalanov broj
rekurzija za Catalanove brojeve
- algebarski dokaz FUI
ovo nisam bila osobno prisutna
- dokazati binomnu formulu indukcijom
- dokazati svojstvo apsorpcije binomnih koeficijenata r* (n povrh r) = n* (n-1 povrh r-1)
- zadnji tm (o rac. FjamaIz) osnovna svojstva rac FjaIz
to su sva pitanja
zbilja mi se neda pisati odgovore
no, ako nije nesto jasno (sto se trazi, ili koje je rjesenje - ono, kopate po biljeskama i udzbeniku i nemrete nac  ), mogu pogledati u biljeskama s usmenog i probati pronaci (nisu bas sva pitanja odgovorena...) ), mogu pogledati u biljeskama s usmenog i probati pronaci (nisu bas sva pitanja odgovorena...)
ako ima greska, pitajte, moglo je doci do tipfelera (kojima sam ja po difoltu skolna  ) )
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
Perosito
Forumaš(ica)

Pridružen/a: 30. 01. 2004. (22:21:16)
Postovi: (7E)16
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 20:04 pon, 16. 2. 2004 Naslov: Postano: 20:04 pon, 16. 2. 2004 Naslov: |
    |
|
|
[quote="Perosito"]Hvala Nesi! Jel možda postoji kakva skripta? I ak ima di se može naći?[/quote]
AFAIK ne...
ono, koiko vidjeh, biljeske s predavanja su sasvim dovoljne za ovaj usmeni :weee:
ali, dobre biljeske :g:
a ako te bas nes vise zanima, knjiga/e od prof.Veljana, prof. Nogo je radila po ovoj novijoj, u izdanju Algoritma
| Perosito (napisa): | | Hvala Nesi! Jel možda postoji kakva skripta? I ak ima di se može naći? |
AFAIK ne...
ono, koiko vidjeh, biljeske s predavanja su sasvim dovoljne za ovaj usmeni 
ali, dobre biljeske 
a ako te bas nes vise zanima, knjiga/e od prof.Veljana, prof. Nogo je radila po ovoj novijoj, u izdanju Algoritma
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
grizko
Forumaš(ica)

Pridružen/a: 19. 02. 2004. (23:21:26)
Postovi: (6)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 23:29 uto, 6. 7. 2004 Naslov: Postano: 23:29 uto, 6. 7. 2004 Naslov: |
    |
|
|
[quote="grizko"]Pliz Nesi,
kako se dokazuje bijekcija u 1. pitanju koje si navela?
Puno hvala. :?[/quote]
(n k) := (n povrh k)
(n r)(r k) je isto sto i prvo odabrati r clani podskup i onda k clani podskup od tog skupa.
Primjetiti da to nije isto kao i odabrati direktno k-clani podskup (jer se ne broje svi oni silni r podskupovi koje smo prvo odabrali). Zato cemo uz taj k-clani skup uzeti i ostatak elemenata koji nam treba da popunimo "pocetni" r-clani skup. Tj. idemo unatrag.
Umjesto da smo prvo uzeli r-clani podskup i njegov k-clani podskup, mi prvo uzeli k-clani podskup i popunili ga do r-clanog podskupa :D
(n r)(r k)=(n k)(n-k r-k) :)
| grizko (napisa): | Pliz Nesi,
kako se dokazuje bijekcija u 1. pitanju koje si navela?
Puno hvala.  |
(n k) := (n povrh k)
(n r)(r k) je isto sto i prvo odabrati r clani podskup i onda k clani podskup od tog skupa.
Primjetiti da to nije isto kao i odabrati direktno k-clani podskup (jer se ne broje svi oni silni r podskupovi koje smo prvo odabrali). Zato cemo uz taj k-clani skup uzeti i ostatak elemenata koji nam treba da popunimo "pocetni" r-clani skup. Tj. idemo unatrag.
Umjesto da smo prvo uzeli r-clani podskup i njegov k-clani podskup, mi prvo uzeli k-clani podskup i popunili ga do r-clanog podskupa 
(n r)(r k)=(n k)(n-k r-k) 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krtica
Forumaš(ica)

Pridružen/a: 13. 02. 2005. (23:16:38)
Postovi: (2)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Perosito
Forumaš(ica)

Pridružen/a: 30. 01. 2004. (22:21:16)
Postovi: (7E)16
|
 Postano: 11:20 ned, 20. 2. 2005 Naslov: Postano: 11:20 ned, 20. 2. 2005 Naslov: |
    |
|
|
Pa u globalu pita sve, ne radi razlike između dvojke i petice što se pitanja tiče, jedino što za dva ne trebaš znati neke teže dokaze, nego tek otprilike kak idu, npr. poopćeni FUI, posljednji teorem i sl. Obavezno trebaš znati rekurzije, binomne koeficijente, osnovne pojmove iz analize, elementarne i algebre, kombinacije, permutacije i stvari vezane za to itd. Zapravo, ona pita na način da otvori bilježnicu i kaj ti otvori to te pita, s tim da obično na početku pita osnovne bin. koeficijente, da ih nabrojiš i jednog dokažeš. Moj savjet (mada me možda ne treba pretjerano ozbiljno shvaćati, jer sam 3 put pal na usmenom :oops: ) je da proučiš sve, bez nekog preskakanja i ovisno o sreći, snalažljivosti i izboru pitanja ti ovisi prolaz. Isto tak, ak imaš bolju ocjenu na pismenom imaš malo više šansi za prolaz, što ne znači da za dva (ak npr. imaš 4) ne moraš niš znati! I tak... Sretno! :) PS Mislim da ova Krckova teorija s postocima nije baš najbolja, bolje ipak učiti čim, čim više - tim, tim bolje! :neznam: No, tko sam ja da ti sudim...
Pa u globalu pita sve, ne radi razlike između dvojke i petice što se pitanja tiče, jedino što za dva ne trebaš znati neke teže dokaze, nego tek otprilike kak idu, npr. poopćeni FUI, posljednji teorem i sl. Obavezno trebaš znati rekurzije, binomne koeficijente, osnovne pojmove iz analize, elementarne i algebre, kombinacije, permutacije i stvari vezane za to itd. Zapravo, ona pita na način da otvori bilježnicu i kaj ti otvori to te pita, s tim da obično na početku pita osnovne bin. koeficijente, da ih nabrojiš i jednog dokažeš. Moj savjet (mada me možda ne treba pretjerano ozbiljno shvaćati, jer sam 3 put pal na usmenom  ) je da proučiš sve, bez nekog preskakanja i ovisno o sreći, snalažljivosti i izboru pitanja ti ovisi prolaz. Isto tak, ak imaš bolju ocjenu na pismenom imaš malo više šansi za prolaz, što ne znači da za dva (ak npr. imaš 4) ne moraš niš znati! I tak... Sretno! ) je da proučiš sve, bez nekog preskakanja i ovisno o sreći, snalažljivosti i izboru pitanja ti ovisi prolaz. Isto tak, ak imaš bolju ocjenu na pismenom imaš malo više šansi za prolaz, što ne znači da za dva (ak npr. imaš 4) ne moraš niš znati! I tak... Sretno!  PS Mislim da ova Krckova teorija s postocima nije baš najbolja, bolje ipak učiti čim, čim više - tim, tim bolje! PS Mislim da ova Krckova teorija s postocima nije baš najbolja, bolje ipak učiti čim, čim više - tim, tim bolje!  No, tko sam ja da ti sudim... No, tko sam ja da ti sudim...
_________________ Nije sve tako sivo... Kad imaš s nekim otić na pivo  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 15:35 ned, 20. 2. 2005 Naslov: Postano: 15:35 ned, 20. 2. 2005 Naslov: |
    |
|
|
[quote="Perosito"]Mislim da ova Krckova teorija s postocima nije baš najbolja, bolje ipak učiti čim, čim više - tim, tim bolje! :neznam: No, tko sam ja da ti sudim...[/quote]
I ja mislim da mu je to bolje ako zeli poloziti Kombinatoriku. Ali nije nas to pitao, mozda stvarno samo zeli saznati koji je minimum za prolaz :wink:
| Perosito (napisa): | Mislim da ova Krckova teorija s postocima nije baš najbolja, bolje ipak učiti čim, čim više - tim, tim bolje!  No, tko sam ja da ti sudim... No, tko sam ja da ti sudim... |
I ja mislim da mu je to bolje ako zeli poloziti Kombinatoriku. Ali nije nas to pitao, mozda stvarno samo zeli saznati koji je minimum za prolaz 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
amihic
Forumaš(ica)

Pridružen/a: 12. 06. 2005. (14:05:58)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Ema
Forumaš(ica)

Pridružen/a: 01. 02. 2005. (12:44:59)
Postovi: (9C)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 10:07 pet, 3. 2. 2006 Naslov: Postano: 10:07 pet, 3. 2. 2006 Naslov: |
    |
|
|
[quote="Ema"]prvo pita zadatak s FI ako to neznas dalje ne pita.[/quote]
Mene nije pitala, ali u principu pita, i stvarno, ako ne znas, dovidenja kolega. Naime, kako FI nisu ulazile u gradivo kolokvija, profesorica je rekla da zadatke iz tog dijela gradiva pita na usmenom.
Sad to mozda zvuci zastrasujuce, ali barem ona pitanja koja sam ja vidio da profesorica pita su bila prilicno lagana ako si isao na vjezbe redovito i ako si malo to provjezbao. Problem je bio u tome sto ljudi nisu bili uopce spremni na to pa ih je smelo. Najcesce je pitanje bilo da neku rekurziju reda 2 ili 3, sa zadanim pocetnim uvjetima rijesis uz pomoc funkcija izvodnica. Kako to dosta ljudi nije znalo, evo jedan primjer koji ce valjda nekome pomoci:
[latex]a_n = a_{n-1} + 2 a_{n-2} + 1[/latex] uz uvjet [latex]a_0 = 0[/latex], [latex]a_1 = 1[/latex]
Prvo sto raimo je dazapisemo rekurziju u obliku [latex]a_{n+2} = a_{n+1} + 2 a_n + 1[/latex], to radimo da nam se u sumi ne bi pojavili [latex]a_{-2}[/latex] i [latex]a_{-1}[/latex] Tada pomnozimo taj izraz sa [latex]x^n[/latex] i sumiramo po n >= 0.
[latex]\displaystyle \sum_{n \geq 0}a_{n+2}x^n = \sum_{n \geq 0}a_{n+1}x^n + 2 \sum_{n \geq 0}a_n x^n + \sum_{n \geq 0}x^n \\
\Longleftrightarrow \frac{A(x) - a_1x - a_0}{x^2} = \frac{A(x) - a_0}{x} + 2 A(x) + \frac{1}{1 - x} \\
\Longleftrightarrow A(x) \frac{1 - x - 2x^2}{x^2} = \frac{1}{x} + \frac{1}{1-x}[/latex] i sad da ne budem doasadan, izrazi se A(x), pa onda rastav na pracijalne razlomke, i onda dobijes koliki su koef. ali vjerojatno bi te profesorica ovdje prekinula :P
A osim ovoga, profesorica svakog pita puno pitanja, i to dosta napreskokce tako da te pita iz svega pomalo, no pitanja su vecinom lagana, recimo mene je profesorica pitala Eulerovu funkciju, pa dokaz da je rj. linearne homogene rekurzije linearna kombinacija karakteristicnih korijena, broj najbrzih puteva u cjelobrojnoj mrezi iz tocke (0,0) do (p,q), pokazi razna svojstva binomnih koeficijenata, kako se 2n povrh n napise uz pomoc sume, kako smo definirali FI, nesto malo o razumijevanju vektorskog prostora i kolika je njegova dimenzija, broj rjesenja u [latex]N_0[/latex] jednadzbe [latex]x_1 + x_2 + ... + x_r = n[/latex], i vjerojatno jos nesto ali se ne mogu sjetiti.
Dakle, profesorica uglavnom pita laksa pitanja, tek tu i tamo se zalomi nesto teze, ali u principu bi trebao znat odgovoriti na sve sto te pita (mislim da je biloo ako nesto nisi znao, a da nije FI, ocjena manje).
I jos samo upozorenje - kako po faksu kruze glasine da je profesorica nogo na C-u prosle godine na predroku pitala najlakse, a na svakom slijedecem roku sve teze, moguce je da se to dogodi i s kombinatorikom i da na slijedecem roku bude teze.
| Ema (napisa): | | prvo pita zadatak s FI ako to neznas dalje ne pita. |
Mene nije pitala, ali u principu pita, i stvarno, ako ne znas, dovidenja kolega. Naime, kako FI nisu ulazile u gradivo kolokvija, profesorica je rekla da zadatke iz tog dijela gradiva pita na usmenom.
Sad to mozda zvuci zastrasujuce, ali barem ona pitanja koja sam ja vidio da profesorica pita su bila prilicno lagana ako si isao na vjezbe redovito i ako si malo to provjezbao. Problem je bio u tome sto ljudi nisu bili uopce spremni na to pa ih je smelo. Najcesce je pitanje bilo da neku rekurziju reda 2 ili 3, sa zadanim pocetnim uvjetima rijesis uz pomoc funkcija izvodnica. Kako to dosta ljudi nije znalo, evo jedan primjer koji ce valjda nekome pomoci:
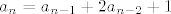 uz uvjet uz uvjet 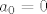 , , 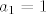
Prvo sto raimo je dazapisemo rekurziju u obliku 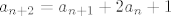 , to radimo da nam se u sumi ne bi pojavili , to radimo da nam se u sumi ne bi pojavili 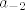 i i  Tada pomnozimo taj izraz sa Tada pomnozimo taj izraz sa 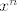 i sumiramo po n >= 0. i sumiramo po n >= 0.
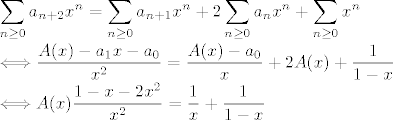 i sad da ne budem doasadan, izrazi se A(x), pa onda rastav na pracijalne razlomke, i onda dobijes koliki su koef. ali vjerojatno bi te profesorica ovdje prekinula i sad da ne budem doasadan, izrazi se A(x), pa onda rastav na pracijalne razlomke, i onda dobijes koliki su koef. ali vjerojatno bi te profesorica ovdje prekinula 
A osim ovoga, profesorica svakog pita puno pitanja, i to dosta napreskokce tako da te pita iz svega pomalo, no pitanja su vecinom lagana, recimo mene je profesorica pitala Eulerovu funkciju, pa dokaz da je rj. linearne homogene rekurzije linearna kombinacija karakteristicnih korijena, broj najbrzih puteva u cjelobrojnoj mrezi iz tocke (0,0) do (p,q), pokazi razna svojstva binomnih koeficijenata, kako se 2n povrh n napise uz pomoc sume, kako smo definirali FI, nesto malo o razumijevanju vektorskog prostora i kolika je njegova dimenzija, broj rjesenja u 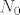 jednadzbe jednadzbe  , i vjerojatno jos nesto ali se ne mogu sjetiti. , i vjerojatno jos nesto ali se ne mogu sjetiti.
Dakle, profesorica uglavnom pita laksa pitanja, tek tu i tamo se zalomi nesto teze, ali u principu bi trebao znat odgovoriti na sve sto te pita (mislim da je biloo ako nesto nisi znao, a da nije FI, ocjena manje).
I jos samo upozorenje - kako po faksu kruze glasine da je profesorica nogo na C-u prosle godine na predroku pitala najlakse, a na svakom slijedecem roku sve teze, moguce je da se to dogodi i s kombinatorikom i da na slijedecem roku bude teze.
_________________
Bri
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 16:54 sub, 4. 2. 2006 Naslov: Postano: 16:54 sub, 4. 2. 2006 Naslov: |
    |
|
|
Sve što je Grga rekao stoji: profesorica te ispita sve uzduž i poprijeko, 20-ak minuta, s tim što je na većinu pitanja odgovor kratak pa to ispadne 10-15 kratkih pitanja, par minuta svako, samo da vidi da kužiš i ne pila dalje previše. Što će reći, pusti te do kraja da raspišeš što imaš pa te tek onda hapa za moguće greške, a ni tu nije prestrašno ak vidi da kužiš. Jedan kolega je zabunom u formuli zamijenio indekse, a vidjelo se da shvaća i dobro je objasnio, i profesorica se nije ni osvrnula na to.
Ja isto nisam dobio rekurziju za riješit pomoću FI, ali me ispitala druge stvari iz toga (mislim da nema smisla nabrajati pitanja, kad stvarno pita sve).
Isto tako, nisam nazočio niti jednom rušenju, pa ne mogu komentirati, ali profesorica stvano nije bauk i lijepo pita i relativno je ugodno kod nje odgovarat.
Eto, nadam se da je nekom pomoglo. I, naravno, sretno svima koji će tek izaći na ispit :w
Sve što je Grga rekao stoji: profesorica te ispita sve uzduž i poprijeko, 20-ak minuta, s tim što je na većinu pitanja odgovor kratak pa to ispadne 10-15 kratkih pitanja, par minuta svako, samo da vidi da kužiš i ne pila dalje previše. Što će reći, pusti te do kraja da raspišeš što imaš pa te tek onda hapa za moguće greške, a ni tu nije prestrašno ak vidi da kužiš. Jedan kolega je zabunom u formuli zamijenio indekse, a vidjelo se da shvaća i dobro je objasnio, i profesorica se nije ni osvrnula na to.
Ja isto nisam dobio rekurziju za riješit pomoću FI, ali me ispitala druge stvari iz toga (mislim da nema smisla nabrajati pitanja, kad stvarno pita sve).
Isto tako, nisam nazočio niti jednom rušenju, pa ne mogu komentirati, ali profesorica stvano nije bauk i lijepo pita i relativno je ugodno kod nje odgovarat.
Eto, nadam se da je nekom pomoglo. I, naravno, sretno svima koji će tek izaći na ispit 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 17:45 sub, 4. 2. 2006 Naslov: Postano: 17:45 sub, 4. 2. 2006 Naslov: |
    |
|
|
cuo sam da su ljudi padali ako su kod FI rekli npr da je
[latex]\sum_{n>=0} x^{n+3}= 1/(1-x^3)[/latex] i slicne stvari..
meni je bio jedan od ugodnijih ispita, ko sto su ostali rekli puno pitanja, ali nigdje nikakvo inzistiranje na detaljima, bitno je pokazati razumijevanje.
'zadatak' mi je bio kako bih odredio na koliko nacina mogu dobiti 45 bodova ako pisem test sa 5 zadataka po 10 bodova.
samo sam napisao FI i to je sve.
ostala pitanja:
iskazati teorem o pravim racionalnim FI
cauchyev identitet izvesti iz permutacija
definirati eksponencijalnu EFI, sto ako je niz 1,1,1,..
rekurziju za broj deranzmana, onu drugogog reda
i jel znam koja je EFI za deranzmane, samo funkciju napisati
tolko se sjecam.. sad mi se cini malo pitanja, mozda je bilo jos nesto
sretno
cuo sam da su ljudi padali ako su kod FI rekli npr da je
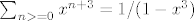 i slicne stvari.. i slicne stvari..
meni je bio jedan od ugodnijih ispita, ko sto su ostali rekli puno pitanja, ali nigdje nikakvo inzistiranje na detaljima, bitno je pokazati razumijevanje.
'zadatak' mi je bio kako bih odredio na koliko nacina mogu dobiti 45 bodova ako pisem test sa 5 zadataka po 10 bodova.
samo sam napisao FI i to je sve.
ostala pitanja:
iskazati teorem o pravim racionalnim FI
cauchyev identitet izvesti iz permutacija
definirati eksponencijalnu EFI, sto ako je niz 1,1,1,..
rekurziju za broj deranzmana, onu drugogog reda
i jel znam koja je EFI za deranzmane, samo funkciju napisati
tolko se sjecam.. sad mi se cini malo pitanja, mozda je bilo jos nesto
sretno
|
|
| [Vrh] |
|
apezic
Forumaš(ica)


Pridružen/a: 18. 10. 2005. (15:43:48)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
|












