|
[b]Taylorov teorem.[/b]
Neka je [latex]A \subseteq \mathbb{R}^n[/latex] otvoren, te neka je [latex]f : A \to R[/latex] klase [latex]C^{k+1}[/latex].
Neka su [latex]x \in A[/latex], te [latex]0 \neq h \in \mathbb{R}^n[/latex] takvi da je [latex]\left[x,\, x+h\right] \subset A[/latex].
Tada postoji [latex]\lambda \in \left[0,\, 1\right][/latex] takav da je
[latex]f\left(x+h\right)=\sum\limits_{i=0}^{k}{\frac{1}{i!} \mathrm{D}^if\left(x\right)\left(h,\, \ldots,\, h\right)} + \frac{1}{\left(k+1\right)!}\mathrm{D}^{k+1}f\left(x+\lambda h\right)\left(h,\, \ldots,\, h\right)[/latex].
Sada prelazimo na ono što je nama bitno. :)
U iskazu teorema također stoji sljedeće:
Neka je [latex]h=\left(h_1,\, h_2,\, \ldots,\, h_n\right)[/latex].
[b]Polinom u varijablama [latex]h_1,\, h_2,\, \ldots,\, h_n[/latex]
[latex]T_k\left(x,\, h\right)=\sum\limits_{i=0}^{k}{\frac{1}{i!} \mathrm{D}^if\left(x\right)\left(h,\, \ldots,\, h\right)}[/latex]
naziva se Taylorov polinom stupnja [latex]k[/latex].[/b]
Dakle, oblik ostatka Taylorovog polinoma [latex]T_k\left(x,\, h\right)[/latex] je
[latex]\frac{1}{\left(k+1\right)!}\mathrm{D}^{k+1}f\left(x+\lambda h\right)\left(h,\, \ldots,\, h\right)[/latex].
Pokažimo to na primjeru.
[b]Zadatak.[/b] (6. [url=http://web.math.hr/nastava/difraf/z2009.pdf]ovdje[/url])
Odredite Taylorov polinom 2. stupnja oko točke [latex]\left(0,\, 0,\, 0\right)[/latex] za funkciju
[latex]f\left(x,\, y,\, z\right) = e^{x+y^2+z^3}[/latex]
(raspišite ga do kraja). [b]Napišite oblik ostatka, bez računanja 3. diferencijala.[/b]
[b]Rješenje.[/b]
[latex]T_2\left(0,\, h\right)= 1 + h_1 + \frac{1}{2}\left(h_1^2 + h_2^2\right)[/latex].
[latex]R = \frac{1}{3!}\mathrm{D}^3f\left(\lambda h\right)\left(h,\, h,\, h\right)[/latex], ovdje je [latex]\lambda \in \left[0,\, 1\right][/latex].
Naime, u zadatku vam kaže, [b]bez računanja 3. diferencijala[/b]. To znači da možete napisati ovako kako sam napisao, ukoliko bi pisalo samo da se napiše ostatak, onda bi bilo potrebno izračunati [latex]\mathrm{D}^3f\left(\lambda h\right)[/latex].
Nadam se da sam uspio razjasniti. :)
Taylorov teorem.
Neka je 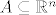 otvoren, te neka je otvoren, te neka je 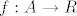 klase klase 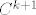 . .
Neka su 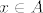 , te , te 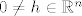 takvi da je takvi da je 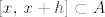 . .
Tada postoji 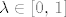 takav da je takav da je
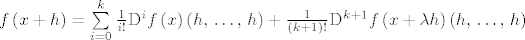 . .
Sada prelazimo na ono što je nama bitno. 
U iskazu teorema također stoji sljedeće:
Neka je 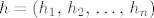 . .
Polinom u varijablama 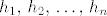
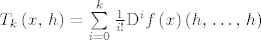
naziva se Taylorov polinom stupnja  . .
Dakle, oblik ostatka Taylorovog polinoma 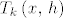 je je
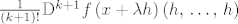 . .
Pokažimo to na primjeru.
Zadatak. (6. ovdje)
Odredite Taylorov polinom 2. stupnja oko točke 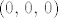 za funkciju za funkciju
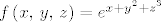
(raspišite ga do kraja). Napišite oblik ostatka, bez računanja 3. diferencijala.
Rješenje.
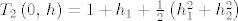 . .
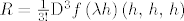 , ovdje je , ovdje je 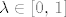 . .
Naime, u zadatku vam kaže, bez računanja 3. diferencijala. To znači da možete napisati ovako kako sam napisao, ukoliko bi pisalo samo da se napiše ostatak, onda bi bilo potrebno izračunati 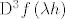 . .
Nadam se da sam uspio razjasniti. 
|





