| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
matz
Forumaš(ica)

Pridružen/a: 26. 01. 2010. (07:47:49)
Postovi: (1)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 22:46 uto, 26. 1. 2010 Naslov: Postano: 22:46 uto, 26. 1. 2010 Naslov: |
    |
|
|
[quote="Tomy007"]Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N --> S. Pročitao sam to u Guljašovoj skripti ali nisam to uspio razumiti. I kako bi onda koristeći ovu tvrdnju za prebrojivost dokazali da je interval [0,1] (podskup od R) neprebrojiv skup (isto postoji sličan dokaz u skripti strana 39, teorem 1.10 ali nije mi jasan).[/quote]
Definicija prebrojivog skupa je da je ekvipotentan s N.
A da pokazes da ne postoji bijekcija iz N u <0, 1], pokazes kontradikcijom:
Pretpostavimo da postoji bijekcija, tada mozemo sve brojeve iz tog intervala poredati u niz, i koristimo decimalni zapis brojeva s beskonacno mnogo znamenaka devetki (0.5 = 0.4999999...)
[latex]0.x_1^1x_2^1x_3^1\ldots[/latex] , [latex]0.x_1^2x_2^2x_3^2\ldots[/latex] , [latex]0.x_1^3x_2^3x_3^3\ldots[/latex] , itd.
Sad promatramo broj [latex]0.y_1y_2y_3\ldots[/latex] takav da je [latex]y_i = \begin{cases} 2 , ako & x_i^i = 1 \\
1 , inace.\end{cases}[/latex]
Tako definiran broj je razlicit od svih pobrojanih brojeva (jer se od i-tog broja razlikuje u i-toj decimali), a ocito je element od <0, 1], pa smo dobili kontradikciju s tvrdnjom da je nasa funkcija bijekcija jer nije surjekcija.
<0, 1] je ekvipotentan s [0, 1], pa ni [0, 1] ne moze biti ekvipotentan s N jer je ekvipotentnost tranzitivna
| Tomy007 (napisa): | | Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N → S. Pročitao sam to u Guljašovoj skripti ali nisam to uspio razumiti. I kako bi onda koristeći ovu tvrdnju za prebrojivost dokazali da je interval [0,1] (podskup od R) neprebrojiv skup (isto postoji sličan dokaz u skripti strana 39, teorem 1.10 ali nije mi jasan). |
Definicija prebrojivog skupa je da je ekvipotentan s N.
A da pokazes da ne postoji bijekcija iz N u <0, 1], pokazes kontradikcijom:
Pretpostavimo da postoji bijekcija, tada mozemo sve brojeve iz tog intervala poredati u niz, i koristimo decimalni zapis brojeva s beskonacno mnogo znamenaka devetki (0.5 = 0.4999999...)
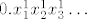 , , 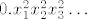 , , 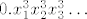 , itd. , itd.
Sad promatramo broj 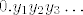 takav da je takav da je 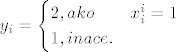
Tako definiran broj je razlicit od svih pobrojanih brojeva (jer se od i-tog broja razlikuje u i-toj decimali), a ocito je element od <0, 1], pa smo dobili kontradikciju s tvrdnjom da je nasa funkcija bijekcija jer nije surjekcija.
<0, 1] je ekvipotentan s [0, 1], pa ni [0, 1] ne moze biti ekvipotentan s N jer je ekvipotentnost tranzitivna
_________________
Bri
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 9:03 sri, 27. 1. 2010 Naslov: Postano: 9:03 sri, 27. 1. 2010 Naslov: |
    |
|
|
[quote="Tomy007"]Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N --> S.[/quote]
Bijekcija je funkcija koja je injekcija i surjekcija, dakle pridružuje po principu 1-1 (tj svakom iz domene pridruži točno jednog iz kodomene i obrnuto). Znači da ih u kodomeni ima jednako mnogo ko u domeni.
primjer:
A={1,2,3,4,5,6}
B={A,B,C,D,E,F}
jedna bijekcija f:A -> B je dana s:
f(1)=A , f(2)=B, f(3)=C, f(4)=D , f(5)=E , f(6)=F
Nije teško vidjeti da je ova funkcija bijekcija, pa skupovi A i B imaju jednako mnogo elemenata.
| Tomy007 (napisa): | | Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N → S. |
Bijekcija je funkcija koja je injekcija i surjekcija, dakle pridružuje po principu 1-1 (tj svakom iz domene pridruži točno jednog iz kodomene i obrnuto). Znači da ih u kodomeni ima jednako mnogo ko u domeni.
primjer:
A={1,2,3,4,5,6}
B={A,B,C,D,E,F}
jedna bijekcija f:A → B je dana s:
f(1)=A , f(2)=B, f(3)=C, f(4)=D , f(5)=E , f(6)=F
Nije teško vidjeti da je ova funkcija bijekcija, pa skupovi A i B imaju jednako mnogo elemenata.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 9:16 sri, 27. 1. 2010 Naslov: Postano: 9:16 sri, 27. 1. 2010 Naslov: |
    |
|
|
[quote="Luuka"][quote="Tomy007"]Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N --> S.[/quote]
Bijekcija je funkcija koja je injekcija i surjekcija, dakle pridružuje po principu 1-1 (tj svakom iz domene pridruži točno jednog iz kodomene i obrnuto). Znači da ih u kodomeni ima jednako mnogo ko u domeni.
primjer:
A={1,2,3,4,5,6}
B={A,B,C,D,E,F}
jedna bijekcija f:A -> B je dana s:
f(1)=A , f(2)=B, f(3)=C, f(4)=D , f(5)=E , f(6)=F
Nije teško vidjeti da je ova funkcija bijekcija, pa skupovi A i B imaju jednako mnogo elemenata.[/quote]
Znam što je bijekcija ali ne mogu pojmiti tu prebrojivost. Osobina skupa N je da uvijek postoji n+1. I onda kako card(N) može biti n, ja to odmah pobijem indukcijom: ako je n u N e pa onda je i n+1 U N i card(N) nije n. Isto tako dokaz da je interval [0,1] neprebrojiv mi je isto apsurdan. Ako čemo gledati bijekciju u N, a N je beskonačan skup, uvijek mogu naći n+1 koji će biti u intervalu [0,1/n] kolko god ja taj interval smanjivao i smanjivao. Mislim znam da je interval [0,1] neprebrojv ali meni je isto neprebrojivo i skup N i skup parnih brojeva i skup neparnih i skup Q i ostali takozvani prebrojivi. Ima li netko da bi mi mogao ovo nekako približiti i izreći na jeziku primjerenu brucošu koji se tek sad upoznava sa pravom matematikom i dokazma. Hvala.
| Luuka (napisa): | | Tomy007 (napisa): | | Može li mi netko objasniti zašto je skup S prebrojiv ako je ekvipotentan skupu prirodnih brojeva N tj. ako postoji bijekcija f: N → S. |
Bijekcija je funkcija koja je injekcija i surjekcija, dakle pridružuje po principu 1-1 (tj svakom iz domene pridruži točno jednog iz kodomene i obrnuto). Znači da ih u kodomeni ima jednako mnogo ko u domeni.
primjer:
A={1,2,3,4,5,6}
B={A,B,C,D,E,F}
jedna bijekcija f:A → B je dana s:
f(1)=A , f(2)=B, f(3)=C, f(4)=D , f(5)=E , f(6)=F
Nije teško vidjeti da je ova funkcija bijekcija, pa skupovi A i B imaju jednako mnogo elemenata. |
Znam što je bijekcija ali ne mogu pojmiti tu prebrojivost. Osobina skupa N je da uvijek postoji n+1. I onda kako card(N) može biti n, ja to odmah pobijem indukcijom: ako je n u N e pa onda je i n+1 U N i card(N) nije n. Isto tako dokaz da je interval [0,1] neprebrojiv mi je isto apsurdan. Ako čemo gledati bijekciju u N, a N je beskonačan skup, uvijek mogu naći n+1 koji će biti u intervalu [0,1/n] kolko god ja taj interval smanjivao i smanjivao. Mislim znam da je interval [0,1] neprebrojv ali meni je isto neprebrojivo i skup N i skup parnih brojeva i skup neparnih i skup Q i ostali takozvani prebrojivi. Ima li netko da bi mi mogao ovo nekako približiti i izreći na jeziku primjerenu brucošu koji se tek sad upoznava sa pravom matematikom i dokazma. Hvala.
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 9:43 sri, 27. 1. 2010 Naslov: Postano: 9:43 sri, 27. 1. 2010 Naslov: |
    |
|
|
Prvo te moram pitati što ti znači kad napišeš [latex]\mathrm{card} (\mathbb{N})=n[/latex] - to nije točno niti za jedan (recimo prirodan ili uopće "normalan", da me ne bi hvatali za detalje :D) broj [latex]n[/latex]. Naime, [latex]\mathrm{card} (\mathbb{N})=\aleph_0[/latex], što nije broj u "normalnom" smislu te riječi. Upravo zato što, a to i ti spominješ, [latex]n\in\mathbb{N}\Rightarrow n+1\in\mathbb{N}[/latex], zaključujemo da ima beskonačno mnogo prirodnih brojeva.
Relativno prirodno razmišljanje o brojanju konačnih skupova (tu priču si sigurno čuo - kad brojiš npr. olovke, onda zapravo jednoj pridružiš broj [latex]1[/latex], drugoj broj [latex]2[/latex] itd.) nas je dovelo do ideje o bijektivnosti kao svojevrsnoj ocjeni koliko ima elemenata u skupovima.
Prirodno je pomisliti da u svim beskonačnim skupovima ima jednako elemenata (jer ih je... hm... beskonačno :D), ali u nekom trenutku ispalo je korisno da probamo iskoristiti ovu našu prirodnu ideju o bijektivnosti (koju i inače koristimo pri brojanju konačnih skupova, npr. u brojnim zadacima u kombinatorici) kao svojstvu skupova jednake veličine da nekako podijelimo beskonačne skupove u klase, ovisno o njihovoj "brojnosti" - to su ti legendarni alefi :).
Ovaj naziv "prebrojivi" i "neprebrojivi" skupovi vjerojatno ne trebaš shvaćati potpuno doslovno :), naravno da ne možeš prebrojati "do kraja" ni prirodne ni realne brojeve - stvar je u tome da prebrojive skupove možeš nekako poredati (Ne nužno po veličini, nego tako da kažeš "ovaj broj je prvi, ovaj broj je drugi itd." - dakle, kao da ih ideš brojati... samo što nikad nećeš doći do kraja :P. No, možeš definirati funkciju koja će ti za bilo koji broj reći koji je on "po redu" i obratno.), a neprebrojive ne možeš.
Ovaj argument s [latex]\displaystyle \[0,\frac{1}{n}\][/latex] i [latex]n+1[/latex] ne shvaćam baš potpuno - ne shvaćam što znači "uvijek mogu naći n+1 koji će biti u intervalu [0,1/n]". Za svaki [latex]n[/latex], [latex]n+1[/latex] je dosta jasno shvaćen i za sve prirodne [latex]n[/latex] vrijedi da je [latex]n+1[/latex] van intervala [latex]\displaystyle \[0,\frac{1}{n}\][/latex]. Sad, ja ne znam želiš li ti ući u diskusiju o tome što je zaista broj i kako mi možemo mijenjati ulogu brojeva itd., ali ako razgovaramo o našem "općeprihvaćenom" sustavu prirodnih i realnih brojeva, onda je to tako :).
Ako si htio reći da u svakom intervalu [latex]\displaystyle \[0,\frac{1}{n}\][/latex] postoji [latex]\displaystyle \frac{1}{n+1}[/latex], to je nedvojbeno, ali ne govori ništa o tome koliko ima prirodnih brojeva (eventualno da ih ima beskonačno, ali i tu možda dolazimo do neke cirkularnosti).
U svakom slučaju, najkraće (i vjerojatno najtočnije) objašnjenje bi bilo da su prebrojivost i neprebrojivost naprosto na neki (vrlo precizan, to s bijekcijama) način definirana svojstva - stoga je malo upitno tražiti objašnjenje zašto je nešto prebrojivo ako zadovoljava baš definiciju prebrojivosti :P. Kao što rekoh, jasno je da prebrojive skupove nikad nećeš moći fizički prebrojati od početka do kraja, ali ćeš uvijek moći definirati funkciju kojom ćeš ih nekako "poredati" i znati koji je koji broj u tom poretku. U tom smislu je dokaz da je [latex]\[0,1\][/latex] neprebrojiv posve točan - mi nikako ne možemo uspostaviti bijekciju između tog skupa i skupa [latex]\mathbb{N}[/latex], što je upravo definicija neprebrojivosti.
Uff, što sam puno napisao... nadam se da sve ovo ima smisla :).
Prvo te moram pitati što ti znači kad napišeš 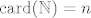 - to nije točno niti za jedan (recimo prirodan ili uopće "normalan", da me ne bi hvatali za detalje - to nije točno niti za jedan (recimo prirodan ili uopće "normalan", da me ne bi hvatali za detalje  ) broj ) broj  . Naime, . Naime, 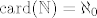 , što nije broj u "normalnom" smislu te riječi. Upravo zato što, a to i ti spominješ, , što nije broj u "normalnom" smislu te riječi. Upravo zato što, a to i ti spominješ, 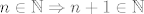 , zaključujemo da ima beskonačno mnogo prirodnih brojeva. , zaključujemo da ima beskonačno mnogo prirodnih brojeva.
Relativno prirodno razmišljanje o brojanju konačnih skupova (tu priču si sigurno čuo - kad brojiš npr. olovke, onda zapravo jednoj pridružiš broj  , drugoj broj , drugoj broj  itd.) nas je dovelo do ideje o bijektivnosti kao svojevrsnoj ocjeni koliko ima elemenata u skupovima. itd.) nas je dovelo do ideje o bijektivnosti kao svojevrsnoj ocjeni koliko ima elemenata u skupovima.
Prirodno je pomisliti da u svim beskonačnim skupovima ima jednako elemenata (jer ih je... hm... beskonačno  ), ali u nekom trenutku ispalo je korisno da probamo iskoristiti ovu našu prirodnu ideju o bijektivnosti (koju i inače koristimo pri brojanju konačnih skupova, npr. u brojnim zadacima u kombinatorici) kao svojstvu skupova jednake veličine da nekako podijelimo beskonačne skupove u klase, ovisno o njihovoj "brojnosti" - to su ti legendarni alefi ), ali u nekom trenutku ispalo je korisno da probamo iskoristiti ovu našu prirodnu ideju o bijektivnosti (koju i inače koristimo pri brojanju konačnih skupova, npr. u brojnim zadacima u kombinatorici) kao svojstvu skupova jednake veličine da nekako podijelimo beskonačne skupove u klase, ovisno o njihovoj "brojnosti" - to su ti legendarni alefi  . .
Ovaj naziv "prebrojivi" i "neprebrojivi" skupovi vjerojatno ne trebaš shvaćati potpuno doslovno  , naravno da ne možeš prebrojati "do kraja" ni prirodne ni realne brojeve - stvar je u tome da prebrojive skupove možeš nekako poredati (Ne nužno po veličini, nego tako da kažeš "ovaj broj je prvi, ovaj broj je drugi itd." - dakle, kao da ih ideš brojati... samo što nikad nećeš doći do kraja , naravno da ne možeš prebrojati "do kraja" ni prirodne ni realne brojeve - stvar je u tome da prebrojive skupove možeš nekako poredati (Ne nužno po veličini, nego tako da kažeš "ovaj broj je prvi, ovaj broj je drugi itd." - dakle, kao da ih ideš brojati... samo što nikad nećeš doći do kraja  . No, možeš definirati funkciju koja će ti za bilo koji broj reći koji je on "po redu" i obratno.), a neprebrojive ne možeš. . No, možeš definirati funkciju koja će ti za bilo koji broj reći koji je on "po redu" i obratno.), a neprebrojive ne možeš.
Ovaj argument s 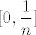 i i 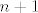 ne shvaćam baš potpuno - ne shvaćam što znači "uvijek mogu naći n+1 koji će biti u intervalu [0,1/n]". Za svaki ne shvaćam baš potpuno - ne shvaćam što znači "uvijek mogu naći n+1 koji će biti u intervalu [0,1/n]". Za svaki  , , 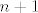 je dosta jasno shvaćen i za sve prirodne je dosta jasno shvaćen i za sve prirodne  vrijedi da je vrijedi da je 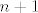 van intervala van intervala 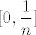 . Sad, ja ne znam želiš li ti ući u diskusiju o tome što je zaista broj i kako mi možemo mijenjati ulogu brojeva itd., ali ako razgovaramo o našem "općeprihvaćenom" sustavu prirodnih i realnih brojeva, onda je to tako . Sad, ja ne znam želiš li ti ući u diskusiju o tome što je zaista broj i kako mi možemo mijenjati ulogu brojeva itd., ali ako razgovaramo o našem "općeprihvaćenom" sustavu prirodnih i realnih brojeva, onda je to tako  . .
Ako si htio reći da u svakom intervalu 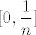 postoji postoji 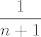 , to je nedvojbeno, ali ne govori ništa o tome koliko ima prirodnih brojeva (eventualno da ih ima beskonačno, ali i tu možda dolazimo do neke cirkularnosti). , to je nedvojbeno, ali ne govori ništa o tome koliko ima prirodnih brojeva (eventualno da ih ima beskonačno, ali i tu možda dolazimo do neke cirkularnosti).
U svakom slučaju, najkraće (i vjerojatno najtočnije) objašnjenje bi bilo da su prebrojivost i neprebrojivost naprosto na neki (vrlo precizan, to s bijekcijama) način definirana svojstva - stoga je malo upitno tražiti objašnjenje zašto je nešto prebrojivo ako zadovoljava baš definiciju prebrojivosti  . Kao što rekoh, jasno je da prebrojive skupove nikad nećeš moći fizički prebrojati od početka do kraja, ali ćeš uvijek moći definirati funkciju kojom ćeš ih nekako "poredati" i znati koji je koji broj u tom poretku. U tom smislu je dokaz da je . Kao što rekoh, jasno je da prebrojive skupove nikad nećeš moći fizički prebrojati od početka do kraja, ali ćeš uvijek moći definirati funkciju kojom ćeš ih nekako "poredati" i znati koji je koji broj u tom poretku. U tom smislu je dokaz da je 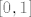 neprebrojiv posve točan - mi nikako ne možemo uspostaviti bijekciju između tog skupa i skupa neprebrojiv posve točan - mi nikako ne možemo uspostaviti bijekciju između tog skupa i skupa  , što je upravo definicija neprebrojivosti. , što je upravo definicija neprebrojivosti.
Uff, što sam puno napisao... nadam se da sve ovo ima smisla  . .
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 9:53 sri, 27. 1. 2010 Naslov: Postano: 9:53 sri, 27. 1. 2010 Naslov: |
    |
|
|
Ne znači ti prebrojivost da postoji neki n el. N takav da je card(skupa) = n.
I N i njemu ekvipotentni (dakle prebrojivi) skupovi imaju naravno beskonačno mnogo elemenata, ali se razlikuju od ostalih beskonačnih skupova: elementi im se mogu učinkovito (iako uzaludno :P) brojati. Možeš uzimati jedan po jedan element skupa, i za bilo koji element skupa biti siguran da ćeš nakon k koraka stići do njega. Npr. u skupu Z je to lako: ako uzmeš niz: 0, -1, 1, 2, -2... možeš biti siguran da ćeš do svakog elementa skupa Z stići nakon otprilike 2|z| koraka, ako je z broj kojeg tražiš. Možeš dakle smislit način da mu učinkovito brojiš elemente, a pod učinkovito mislim tako da tvoj postupak ništa ne izostavlja i da bi kad bi ga pustio u beskonačnost zahvatio sve elemente skupa.
U skupu R je tako nešto nemoguće: ne samo da mu ne možeš izbrojati elemente, nego ih ne možeš ni krenuti prebrojavat, što je formalizirano u dokazu koji je Grga dao. Kako ih god poredaš u niz, uvijek možeš naći neki koji si promašio, pošto je decimalni zapis realnoga broja beskonačan.
Sa skupovima koji imaju kardinalni broj veći i od R je situacija naravno još "gora".
Eto, valjda ovo ima nekog smisla :) Naravno, ovo je sve skroz neformalno, formalno su stvari jednostavnije :D
I naravno, mornik je bio brži :lol:
Ne znači ti prebrojivost da postoji neki n el. N takav da je card(skupa) = n.
I N i njemu ekvipotentni (dakle prebrojivi) skupovi imaju naravno beskonačno mnogo elemenata, ali se razlikuju od ostalih beskonačnih skupova: elementi im se mogu učinkovito (iako uzaludno  ) brojati. Možeš uzimati jedan po jedan element skupa, i za bilo koji element skupa biti siguran da ćeš nakon k koraka stići do njega. Npr. u skupu Z je to lako: ako uzmeš niz: 0, -1, 1, 2, -2... možeš biti siguran da ćeš do svakog elementa skupa Z stići nakon otprilike 2|z| koraka, ako je z broj kojeg tražiš. Možeš dakle smislit način da mu učinkovito brojiš elemente, a pod učinkovito mislim tako da tvoj postupak ništa ne izostavlja i da bi kad bi ga pustio u beskonačnost zahvatio sve elemente skupa. ) brojati. Možeš uzimati jedan po jedan element skupa, i za bilo koji element skupa biti siguran da ćeš nakon k koraka stići do njega. Npr. u skupu Z je to lako: ako uzmeš niz: 0, -1, 1, 2, -2... možeš biti siguran da ćeš do svakog elementa skupa Z stići nakon otprilike 2|z| koraka, ako je z broj kojeg tražiš. Možeš dakle smislit način da mu učinkovito brojiš elemente, a pod učinkovito mislim tako da tvoj postupak ništa ne izostavlja i da bi kad bi ga pustio u beskonačnost zahvatio sve elemente skupa.
U skupu R je tako nešto nemoguće: ne samo da mu ne možeš izbrojati elemente, nego ih ne možeš ni krenuti prebrojavat, što je formalizirano u dokazu koji je Grga dao. Kako ih god poredaš u niz, uvijek možeš naći neki koji si promašio, pošto je decimalni zapis realnoga broja beskonačan.
Sa skupovima koji imaju kardinalni broj veći i od R je situacija naravno još "gora".
Eto, valjda ovo ima nekog smisla  Naravno, ovo je sve skroz neformalno, formalno su stvari jednostavnije Naravno, ovo je sve skroz neformalno, formalno su stvari jednostavnije 
I naravno, mornik je bio brži 
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 10:49 sri, 27. 1. 2010 Naslov: Postano: 10:49 sri, 27. 1. 2010 Naslov: |
    |
|
|
Hvala vam obojici. Ova objašnjenja su mi sad približila taj pojam i sad mi je puno jasnija ta definicija. Ja sam to počeo shvaćati doslovno pa to nisam mogao pojmiti, ali kad se to ovako objasni postaje mnogo lakše za shvatiti. E da @mornik, malo sam zbunio sa onim n+1 koji može ući u [0,1/n),a ustvari sam mislio reći da postoji f(n+1) koji može ući u [0,1/n] ali sad vidim da ni to baš nije moguće zbog beskonačnosti brojeva iza decimalne točke.
Hvala vam obojici. Ova objašnjenja su mi sad približila taj pojam i sad mi je puno jasnija ta definicija. Ja sam to počeo shvaćati doslovno pa to nisam mogao pojmiti, ali kad se to ovako objasni postaje mnogo lakše za shvatiti. E da @mornik, malo sam zbunio sa onim n+1 koji može ući u [0,1/n),a ustvari sam mislio reći da postoji f(n+1) koji može ući u [0,1/n] ali sad vidim da ni to baš nije moguće zbog beskonačnosti brojeva iza decimalne točke.
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 10:52 sri, 27. 1. 2010 Naslov: Postano: 10:52 sri, 27. 1. 2010 Naslov: |
    |
|
|
Izgleda da tebe muci zasto se to [b]zove[/b] prebrojivost. Jednostavno smo te skupove tako nazvali, ne zato sto ih mozemo prebrojati nego zato sto ih mozemo poredati u niz. Skaup je prebrojiv kad postoji bijekcija s N a to je isto kao da kazemo da ih mozemo sve poredati u beskonacan niz i da nijednog necemo promasiti.
Onaj dokaz za neprebrojivost skupa [0, 1] upravo pokazuje to da je realnih brojeva toliko puno da ih je nemoguce poredati u niz a da nekog ne profulas.
Te stvari s beskonacnim skupovima je intuitivno dosta tesko shvatiti jer naravno da nemas prijasnjeg iskustva s njima. Nisam siguran sto si tocno htio s onom pricom o n+1-vom broju koji upada u segment, ali me podsjetilo na ovo:
Skup Q je prebrojiv, to smo pokazali tko da smo definirali jednu bijekciju (sto sad necu pricati kako se radi jer nije vazno ternutacno). Ta bijekcija je funkcija iz N u Q, dakle moze se shvatiti kao niz racionalnih brojeva. E sad tu pocinje ludost - taj niz ima beskonacno mnogo gomilista, tocnije - svaki realan broj je gomiliste tog niza!
Znaci da mozemo napraviti injekciju iz N u R takvu da "pokupimo" beskonacno mnogo brojeva oko svakog realnog broja (iz intervala <x - r, x + r> za r>0 ali proizvoljno mali), ali kako god da to napravimo, nikad ih ne mozemo pokupiti sve.
Jednostavno ces morati neke stvari prihvatiti kao cinjenice:
Postoje skupovi koji su beskonacni.
Ako je skup beskonacan i mozemo napraviti bijekciju izmedu S i N, odnosno skupove iz S mozemo poredati u beskonacan niz tako da nijednog ne izostavimo, tada kazemo da je skup prebrojiv.
Ako je skup beskonacan i nije prebrojiv, tada akzemo da je skup neprebrojiv.
Zapravo stvar sa prebrojivim i neprebrojivim skupovima je slicna prici sa skupom koji ima manje od 5 elemenata i skupom koji ima vise: moguce napraviti surjekciju iz skupa {1, 2, 3, 4, 5} u S, onda S ima manje (ili jednako) od 5 elemenata, ako nije moguce, tada skup ima vise od 5. To ti je jasno jer se radi o konacnim skupovima s kojima vec imas iskustva. No trebas prihvatiti cinjenicu da i za beskonacne skupove postoje oni koji su veci i oni koji su manji, a kriterij za odredivanje koji je veci je potpuno isti kao i za konacne skupove.
Izgleda da tebe muci zasto se to zove prebrojivost. Jednostavno smo te skupove tako nazvali, ne zato sto ih mozemo prebrojati nego zato sto ih mozemo poredati u niz. Skaup je prebrojiv kad postoji bijekcija s N a to je isto kao da kazemo da ih mozemo sve poredati u beskonacan niz i da nijednog necemo promasiti.
Onaj dokaz za neprebrojivost skupa [0, 1] upravo pokazuje to da je realnih brojeva toliko puno da ih je nemoguce poredati u niz a da nekog ne profulas.
Te stvari s beskonacnim skupovima je intuitivno dosta tesko shvatiti jer naravno da nemas prijasnjeg iskustva s njima. Nisam siguran sto si tocno htio s onom pricom o n+1-vom broju koji upada u segment, ali me podsjetilo na ovo:
Skup Q je prebrojiv, to smo pokazali tko da smo definirali jednu bijekciju (sto sad necu pricati kako se radi jer nije vazno ternutacno). Ta bijekcija je funkcija iz N u Q, dakle moze se shvatiti kao niz racionalnih brojeva. E sad tu pocinje ludost - taj niz ima beskonacno mnogo gomilista, tocnije - svaki realan broj je gomiliste tog niza!
Znaci da mozemo napraviti injekciju iz N u R takvu da "pokupimo" beskonacno mnogo brojeva oko svakog realnog broja (iz intervala <x - r, x + r> za r>0 ali proizvoljno mali), ali kako god da to napravimo, nikad ih ne mozemo pokupiti sve.
Jednostavno ces morati neke stvari prihvatiti kao cinjenice:
Postoje skupovi koji su beskonacni.
Ako je skup beskonacan i mozemo napraviti bijekciju izmedu S i N, odnosno skupove iz S mozemo poredati u beskonacan niz tako da nijednog ne izostavimo, tada kazemo da je skup prebrojiv.
Ako je skup beskonacan i nije prebrojiv, tada akzemo da je skup neprebrojiv.
Zapravo stvar sa prebrojivim i neprebrojivim skupovima je slicna prici sa skupom koji ima manje od 5 elemenata i skupom koji ima vise: moguce napraviti surjekciju iz skupa {1, 2, 3, 4, 5} u S, onda S ima manje (ili jednako) od 5 elemenata, ako nije moguce, tada skup ima vise od 5. To ti je jasno jer se radi o konacnim skupovima s kojima vec imas iskustva. No trebas prihvatiti cinjenicu da i za beskonacne skupove postoje oni koji su veci i oni koji su manji, a kriterij za odredivanje koji je veci je potpuno isti kao i za konacne skupove.
_________________
Bri
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 10:59 sri, 27. 1. 2010 Naslov: Postano: 10:59 sri, 27. 1. 2010 Naslov: |
    |
|
|
[quote="Grga"]Izgleda da tebe muci zasto se to [b]zove[/b] prebrojivost. Jednostavno smo te skupove tako nazvali, ne zato sto ih mozemo prebrojati nego zato sto ih mozemo poredati u niz. Skaup je prebrojiv kad postoji bijekcija s N a to je isto kao da kazemo da ih mozemo sve poredati u beskonacan niz i da nijednog necemo promasiti.
Onaj dokaz za neprebrojivost skupa [0, 1] upravo pokazuje to da je realnih brojeva toliko puno da ih je nemoguce poredati u niz a da nekog ne profulas.
Te stvari s beskonacnim skupovima je intuitivno dosta tesko shvatiti jer naravno da nemas prijasnjeg iskustva s njima. Nisam siguran sto si tocno htio s onom pricom o n+1-vom broju koji upada u segment, ali me podsjetilo na ovo:
Skup Q je prebrojiv, to smo pokazali tko da smo definirali jednu bijekciju (sto sad necu pricati kako se radi jer nije vazno ternutacno). Ta bijekcija je funkcija iz N u Q, dakle moze se shvatiti kao niz racionalnih brojeva. E sad tu pocinje ludost - taj niz ima beskonacno mnogo gomilista, tocnije - svaki realan broj je gomiliste tog niza!
Znaci da mozemo napraviti injekciju iz N u R takvu da "pokupimo" beskonacno mnogo brojeva oko svakog realnog broja (iz intervala <x - r, x + r> za r>0 ali proizvoljno mali), ali kako god da to napravimo, nikad ih ne mozemo pokupiti sve.
Jednostavno ces morati neke stvari prihvatiti kao cinjenice:
Postoje skupovi koji su beskonacni.
Ako je skup beskonacan i mozemo napraviti bijekciju izmedu S i N, odnosno skupove iz S mozemo poredati u beskonacan niz tako da nijednog ne izostavimo, tada kazemo da je skup prebrojiv.
Ako je skup beskonacan i nije prebrojiv, tada akzemo da je skup neprebrojiv.
Zapravo stvar sa prebrojivim i neprebrojivim skupovima je slicna prici sa skupom koji ima manje od 5 elemenata i skupom koji ima vise: moguce napraviti surjekciju iz skupa {1, 2, 3, 4, 5} u S, onda S ima manje (ili jednako) od 5 elemenata, ako nije moguce, tada skup ima vise od 5. To ti je jasno jer se radi o konacnim skupovima s kojima vec imas iskustva. No trebas prihvatiti cinjenicu da i za beskonacne skupove postoje oni koji su veci i oni koji su manji, a kriterij za odredivanje koji je veci je potpuno isti kao i za konacne skupove.[/quote]
Hvala, Grga. Evo sad upravo učim nizove i konvergenciju i vidim da ne bi mogao definirati niz na "neprebrojivom" skupu i tu sada riječ prebrojivost dobiva svoj smisao jer ja sad znam da između a1 i aNo postoji konačno elemenata niza tj da je interval od [1,No] prebrojiv a to je prilično važno svojstvo za daljnje shvaćanje konvergencije.
| Grga (napisa): | Izgleda da tebe muci zasto se to zove prebrojivost. Jednostavno smo te skupove tako nazvali, ne zato sto ih mozemo prebrojati nego zato sto ih mozemo poredati u niz. Skaup je prebrojiv kad postoji bijekcija s N a to je isto kao da kazemo da ih mozemo sve poredati u beskonacan niz i da nijednog necemo promasiti.
Onaj dokaz za neprebrojivost skupa [0, 1] upravo pokazuje to da je realnih brojeva toliko puno da ih je nemoguce poredati u niz a da nekog ne profulas.
Te stvari s beskonacnim skupovima je intuitivno dosta tesko shvatiti jer naravno da nemas prijasnjeg iskustva s njima. Nisam siguran sto si tocno htio s onom pricom o n+1-vom broju koji upada u segment, ali me podsjetilo na ovo:
Skup Q je prebrojiv, to smo pokazali tko da smo definirali jednu bijekciju (sto sad necu pricati kako se radi jer nije vazno ternutacno). Ta bijekcija je funkcija iz N u Q, dakle moze se shvatiti kao niz racionalnih brojeva. E sad tu pocinje ludost - taj niz ima beskonacno mnogo gomilista, tocnije - svaki realan broj je gomiliste tog niza!
Znaci da mozemo napraviti injekciju iz N u R takvu da "pokupimo" beskonacno mnogo brojeva oko svakog realnog broja (iz intervala <x - r, x + r> za r>0 ali proizvoljno mali), ali kako god da to napravimo, nikad ih ne mozemo pokupiti sve.
Jednostavno ces morati neke stvari prihvatiti kao cinjenice:
Postoje skupovi koji su beskonacni.
Ako je skup beskonacan i mozemo napraviti bijekciju izmedu S i N, odnosno skupove iz S mozemo poredati u beskonacan niz tako da nijednog ne izostavimo, tada kazemo da je skup prebrojiv.
Ako je skup beskonacan i nije prebrojiv, tada akzemo da je skup neprebrojiv.
Zapravo stvar sa prebrojivim i neprebrojivim skupovima je slicna prici sa skupom koji ima manje od 5 elemenata i skupom koji ima vise: moguce napraviti surjekciju iz skupa {1, 2, 3, 4, 5} u S, onda S ima manje (ili jednako) od 5 elemenata, ako nije moguce, tada skup ima vise od 5. To ti je jasno jer se radi o konacnim skupovima s kojima vec imas iskustva. No trebas prihvatiti cinjenicu da i za beskonacne skupove postoje oni koji su veci i oni koji su manji, a kriterij za odredivanje koji je veci je potpuno isti kao i za konacne skupove. |
Hvala, Grga. Evo sad upravo učim nizove i konvergenciju i vidim da ne bi mogao definirati niz na "neprebrojivom" skupu i tu sada riječ prebrojivost dobiva svoj smisao jer ja sad znam da između a1 i aNo postoji konačno elemenata niza tj da je interval od [1,No] prebrojiv a to je prilično važno svojstvo za daljnje shvaćanje konvergencije.
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
surosev
Forumaš(ica)
Pridružen/a: 20. 01. 2010. (20:08:09)
Postovi: (9)16
|
 Postano: 14:47 čet, 28. 1. 2010 Naslov: Postano: 14:47 čet, 28. 1. 2010 Naslov: |
    |
|
|
=>
Raspiši u definiciji 0<|x-c|<delta i razvoji na dva dijela. Jedan dio će ti biti za limes slijeva, a drugi za limes zdesna (prepoznaš prema definiciji koji je lijevi, a koji desni).
<=
Raspiši si što ti znači da funkcija ima limes slijeva i limes zdnesna. Uzmi minimalni delta i objedini te tvrdnje u jednu. Dakle 0<c-x<delta (za limes slijeva), 0<x-c<delta (za limes zdesna), a to je 0<|x-c|<delta.
Pišem samo "problematični" dio dokaza, bez epsilona i tih gluposti.
=>
Raspiši u definiciji 0<|x-c|<delta i razvoji na dva dijela. Jedan dio će ti biti za limes slijeva, a drugi za limes zdesna (prepoznaš prema definiciji koji je lijevi, a koji desni).
<=
Raspiši si što ti znači da funkcija ima limes slijeva i limes zdnesna. Uzmi minimalni delta i objedini te tvrdnje u jednu. Dakle 0<c-x<delta (za limes slijeva), 0<x-c<delta (za limes zdesna), a to je 0<|x-c|<delta.
Pišem samo "problematični" dio dokaza, bez epsilona i tih gluposti.
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 16:06 čet, 28. 1. 2010 Naslov: Postano: 16:06 čet, 28. 1. 2010 Naslov: |
    |
|
|
surosev ti je manje-više napisao dokaz, samo da još jednu stvar objasnim:
[quote="Tomy007"]Je li limes slijeva kad neki niz an --> c kada n ide u -Inf i limes zdesna je kad niz an -->c kada n ide u +Inf?[/quote]
Ne. Budući da niz ima samo članove [latex]a_1, a_2, \ldots[/latex] (dakle, članove s pozitivnim indeksima), [latex]n\to-\infty[/latex] nema smisla. U oba slučaja [latex]n\to +\infty[/latex], samo što u limesu slijeva imaš ograničenje [latex]a_n<c[/latex] za sve prirodne [latex]n[/latex], a u limesu zdesna imaš obratno, dakle da je [latex]a_n>c[/latex] za sve prirodne [latex]n[/latex]. Ovo "slijeva" i "zdesna" dolazi od pozicije članova niza s obzirom na [latex]c[/latex] na brojevnom pravcu, a ne od "načina kretanja" po tom nizu.
surosev ti je manje-više napisao dokaz, samo da još jednu stvar objasnim:
| Tomy007 (napisa): | | Je li limes slijeva kad neki niz an → c kada n ide u -Inf i limes zdesna je kad niz an →c kada n ide u +Inf? |
Ne. Budući da niz ima samo članove 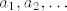 (dakle, članove s pozitivnim indeksima), (dakle, članove s pozitivnim indeksima),  nema smisla. U oba slučaja nema smisla. U oba slučaja 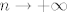 , samo što u limesu slijeva imaš ograničenje , samo što u limesu slijeva imaš ograničenje 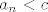 za sve prirodne za sve prirodne  , a u limesu zdesna imaš obratno, dakle da je , a u limesu zdesna imaš obratno, dakle da je 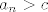 za sve prirodne za sve prirodne  . Ovo "slijeva" i "zdesna" dolazi od pozicije članova niza s obzirom na . Ovo "slijeva" i "zdesna" dolazi od pozicije članova niza s obzirom na  na brojevnom pravcu, a ne od "načina kretanja" po tom nizu. na brojevnom pravcu, a ne od "načina kretanja" po tom nizu.
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
|











