| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
 Postano: 17:41 sri, 27. 1. 2010 Naslov: Postano: 17:41 sri, 27. 1. 2010 Naslov: |
    |
|
|
Ja sam danas bio na usmenom i mogu reć da je profesor super. Opušten je i ne stvara nikakav pritisak. Pita sve baš točno onak kak smo radili i zapisivali.
A što se tiče pitanja, zapravo ih je jako teško sve nabrojat jer profesor pita hrpetinu kratkih pitanja i eventualno jedan dokaz. Doslovno nekih 30ak pitanja u vezi svega šta smo radili.
Mene je između ostalog pitao: što je sustav, kako se matrično interpretira, koji su nužni i dovoljni uvjeti da sustav bude rješiv, kakav je to homogeni sustav, ima li homogeni sustav rješenje i onda naravno opisati ta rješenja, opisati rješenja nehomogenog sustava, koja je metoda rješavanja sustava, što je to potprostor, kako provjeriti da li je nešto potprostor, što je suma potprostora, zašto ju nazivamo sumom, što je direktan komplement, da li svaki potprostor ima direktan komplement, da li je direktan komplement jedinstven, što je regularna matrica, koje su karakterizacije regularnosti...
Mislim da je ovo manje više sve, al nisam siguran. Možda se čini teško, al zbilja nije, sve smo te stvari prošli na prevdavanjima tak da nebi trebalo bit promblema.
Ja sam danas bio na usmenom i mogu reć da je profesor super. Opušten je i ne stvara nikakav pritisak. Pita sve baš točno onak kak smo radili i zapisivali.
A što se tiče pitanja, zapravo ih je jako teško sve nabrojat jer profesor pita hrpetinu kratkih pitanja i eventualno jedan dokaz. Doslovno nekih 30ak pitanja u vezi svega šta smo radili.
Mene je između ostalog pitao: što je sustav, kako se matrično interpretira, koji su nužni i dovoljni uvjeti da sustav bude rješiv, kakav je to homogeni sustav, ima li homogeni sustav rješenje i onda naravno opisati ta rješenja, opisati rješenja nehomogenog sustava, koja je metoda rješavanja sustava, što je to potprostor, kako provjeriti da li je nešto potprostor, što je suma potprostora, zašto ju nazivamo sumom, što je direktan komplement, da li svaki potprostor ima direktan komplement, da li je direktan komplement jedinstven, što je regularna matrica, koje su karakterizacije regularnosti...
Mislim da je ovo manje više sve, al nisam siguran. Možda se čini teško, al zbilja nije, sve smo te stvari prošli na prevdavanjima tak da nebi trebalo bit promblema.
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
bekse
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:19:09)
Postovi: (19)16
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
Kyela
Forumaš(ica)

Pridružen/a: 24. 08. 2009. (23:29:02)
Postovi: (4)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 0:41 čet, 28. 1. 2010 Naslov: Postano: 0:41 čet, 28. 1. 2010 Naslov: |
    |
|
|
[quote="bekse"]Ne, nije jedinstven. Naime direktan komplement potprostora L u vektorskom prostoru V konstruiramo tako da uzmemo proizvoljnu bazu za L i budući da je to linearno nezavisan skup u V, možemo ga nadopuniti do baze za V i onda je upravo prostor razapet elementima kojima smo nadopunili bazu od L do baze za V direktan komplement od L u V pa budući da nadopuna do baze nije jedinstvena, nije ni direktan komplement.[/quote]
Što ako je [latex]V=\{0\}[/latex]? :D
[quote="Black Mamba"]A koji dokaz vas je pita?[/quote]
Rijetko pita dokaze, više iskaze teorema. Mene je pitao dokaz karakterizacije regularnosti preko ranga.
[quote="Kyela"]Imam pitanje. Da li profesor traži određenu definiciju ili neki teorem točno kako ide ili više zahtijeva razumijevanje gradiva?[/quote]
Naglasak je na iskazima definicija i teorema, stvari koje se moraju znati (definicija lin. nezavisnosti, sustav izvodnica, baza, ...). Postavlja puno pitanja koja nadovezuje jedno na drugo, tako da ispitivanje potraje 15-ak min.
| bekse (napisa): | | Ne, nije jedinstven. Naime direktan komplement potprostora L u vektorskom prostoru V konstruiramo tako da uzmemo proizvoljnu bazu za L i budući da je to linearno nezavisan skup u V, možemo ga nadopuniti do baze za V i onda je upravo prostor razapet elementima kojima smo nadopunili bazu od L do baze za V direktan komplement od L u V pa budući da nadopuna do baze nije jedinstvena, nije ni direktan komplement. |
Što ako je 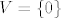 ? ? 
| Black Mamba (napisa): | | A koji dokaz vas je pita? |
Rijetko pita dokaze, više iskaze teorema. Mene je pitao dokaz karakterizacije regularnosti preko ranga.
| Kyela (napisa): | | Imam pitanje. Da li profesor traži određenu definiciju ili neki teorem točno kako ide ili više zahtijeva razumijevanje gradiva? |
Naglasak je na iskazima definicija i teorema, stvari koje se moraju znati (definicija lin. nezavisnosti, sustav izvodnica, baza, ...). Postavlja puno pitanja koja nadovezuje jedno na drugo, tako da ispitivanje potraje 15-ak min.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:43 čet, 28. 1. 2010 Naslov: Postano: 16:43 čet, 28. 1. 2010 Naslov: |
    |
|
|
Pitanja od danas za koja ja znam su sljedeća:
linearna nezavisnost, definicija determinante, regularnost i dokaz da je inverz jedinstven (to je možda novo, ne znam), definicija inverzija, dokaz kod karakterizacije regularnosti pomoću determinante, što je rang matrice...
Zapravo ništa van očekivanog, eventualno ova dva "dokazića", što sam ja informiran.
Pitanja od danas za koja ja znam su sljedeća:
linearna nezavisnost, definicija determinante, regularnost i dokaz da je inverz jedinstven (to je možda novo, ne znam), definicija inverzija, dokaz kod karakterizacije regularnosti pomoću determinante, što je rang matrice...
Zapravo ništa van očekivanog, eventualno ova dva "dokazića", što sam ja informiran.
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 17:44 čet, 28. 1. 2010 Naslov: Postano: 17:44 čet, 28. 1. 2010 Naslov: |
    |
|
|
evo jos nekih pitanja od danas..
:) rang matrice, dokazati da ako je r(A)=r(B)=r, tada su A i B ekvivalentne, linearna ljuska, sistem izvodnica, baza, regularnost, mnozenje matrica, determinanta i tako...
:lol: treba znati samo definicije.. ne treba znati teske dokaze.. ;)
sretno svima :P :lol:
evo jos nekih pitanja od danas..
 rang matrice, dokazati da ako je r(A)=r(B)=r, tada su A i B ekvivalentne, linearna ljuska, sistem izvodnica, baza, regularnost, mnozenje matrica, determinanta i tako... rang matrice, dokazati da ako je r(A)=r(B)=r, tada su A i B ekvivalentne, linearna ljuska, sistem izvodnica, baza, regularnost, mnozenje matrica, determinanta i tako...
 treba znati samo definicije.. ne treba znati teske dokaze.. treba znati samo definicije.. ne treba znati teske dokaze.. 
sretno svima  
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:59 čet, 28. 1. 2010 Naslov: Postano: 21:59 čet, 28. 1. 2010 Naslov: |
    |
|
|
Mene je pitao neš sitno o permutacijama, vezano uz definiciju determinante, al osnove, dakle skup svih permutacija, kako definiramo permutaciju, broj elemenata, nešto malo o inverzijama, ali ništa nepoznato zapravo.
Mene je pitao neš sitno o permutacijama, vezano uz definiciju determinante, al osnove, dakle skup svih permutacija, kako definiramo permutaciju, broj elemenata, nešto malo o inverzijama, ali ništa nepoznato zapravo.
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 23:39 sub, 30. 1. 2010 Naslov: Postano: 23:39 sub, 30. 1. 2010 Naslov: |
    |
|
|
U principu sve već navedeno....
Uglavnom,profesor nadovezuje pitanje na prethodno postavljeno,povezuje gradivo....
Evo,mene je pitao da mu definiram determinantu,što su to permutacije,koliko ima elemenata u skupu permutacija,za koje matrice smo definirali determinantu, kako označavamo te matrice,kako se determinanta ponaša prema elementarnim transformacijama,koje operacije smo definirali na matricama, kako se determinanta ponaša prema tim operacijama (pojasnit odakle te relacije slijede),kako smo karakterizirali regularnost preko determinanti,taj dokaz oba smjera,što je to adjunkta,primjer,kako smo još karakterizirali regularnost (preko ranga) te skicu dokaza,tj odakle to slijedi,zatim što je to linearna nezavisnost,što je baza,što sustav izvodnica,konačnodimenzionalan prostor,kakve su baze u njemu....
Ako imate pojma ikakvog,proći ćete, za ocjenu više treba znati sve što pita i razumjeti....
U principu sve već navedeno....
Uglavnom,profesor nadovezuje pitanje na prethodno postavljeno,povezuje gradivo....
Evo,mene je pitao da mu definiram determinantu,što su to permutacije,koliko ima elemenata u skupu permutacija,za koje matrice smo definirali determinantu, kako označavamo te matrice,kako se determinanta ponaša prema elementarnim transformacijama,koje operacije smo definirali na matricama, kako se determinanta ponaša prema tim operacijama (pojasnit odakle te relacije slijede),kako smo karakterizirali regularnost preko determinanti,taj dokaz oba smjera,što je to adjunkta,primjer,kako smo još karakterizirali regularnost (preko ranga) te skicu dokaza,tj odakle to slijedi,zatim što je to linearna nezavisnost,što je baza,što sustav izvodnica,konačnodimenzionalan prostor,kakve su baze u njemu....
Ako imate pojma ikakvog,proći ćete, za ocjenu više treba znati sve što pita i razumjeti....
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
|













