|
Bilinearna forma nije nista drugo doli bilinearno preslikavanje [latex]B : V \times V \to \mathbb{F}[/latex] gdje je [latex]\mathbb{F}[/latex] polje nad kojim je gradjen [latex]V[/latex].
Bilinearnost znaci da je [latex]B[/latex] linearno u 1. i 2. argumentu zasebno, tj. [latex]B(x + y, z) = B(x,z) + B(y,z), \quad B(x, y+z) = B(x,y) + B(x,z) \\ B(\lambda x, y) = B(x, \lambda y) = \lambda B(x,y)[/latex]
Konkretno, u difrafu promatramo bilinearne forme [latex] B : \mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}[/latex] budući da su izomorfne drugom diferencijalu funkcija [latex]f : A \subseteq \mathbb{R}^n \to \mathbb{R}[/latex] sto nam omogucuje da djelovanje drugog diferencijala nad vektorom identificiramo s operacijama nad matricama.
Ne ulazim u detalje jer je sve manje vise pojasnjeno u skripti, ako ti je nesto konkretno nerazumljivo, reci tocno sto.
Bilinearna forma nije nista drugo doli bilinearno preslikavanje 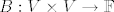 gdje je gdje je 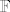 polje nad kojim je gradjen polje nad kojim je gradjen 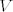 . .
Bilinearnost znaci da je  linearno u 1. i 2. argumentu zasebno, tj. linearno u 1. i 2. argumentu zasebno, tj. 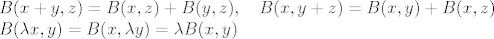
Konkretno, u difrafu promatramo bilinearne forme 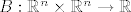 budući da su izomorfne drugom diferencijalu funkcija budući da su izomorfne drugom diferencijalu funkcija 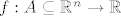 sto nam omogucuje da djelovanje drugog diferencijala nad vektorom identificiramo s operacijama nad matricama. sto nam omogucuje da djelovanje drugog diferencijala nad vektorom identificiramo s operacijama nad matricama.
Ne ulazim u detalje jer je sve manje vise pojasnjeno u skripti, ako ti je nesto konkretno nerazumljivo, reci tocno sto.
|






