| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:25 uto, 16. 3. 2010 Naslov: Postano: 23:25 uto, 16. 3. 2010 Naslov: |
    |
|
|
[latex]\Phi(D)[/latex] je operator (točnije linearni funkcional [latex]f_D[/latex]). Njegova "formula" ti je dana u zadatku. Probaj ne razbijati glavu time kako sve to "izgleda", nego ih promatraj kao i svake druge vektore.
Kao što sam napomenuo gore, možeš dokazati da je skup [latex]S=\{ \Phi(E_{11}), \Phi(E_{12}), \Phi(E_{21}), \Phi(E_{22})\}[/latex] baza za [latex](M_2(\mathbb{R}))^*[/latex]. Dovoljno je pokazati linearnu nezavisnost jer znamo da je [latex]\dim (M_2(\mathbb{R}))^* = 4[/latex]. Uzmeš linearnu kombinaciju tih linearnih funkcionala iz [latex]S[/latex] ([latex]\alpha f_{E_{11}} + \beta f_{E_{12}} + \gamma f_{E_{21}} + \delta f_{E_{22}}[/latex]) i izjednačiš s nulom (tj. pretpostaviš da je nuloperator). No, djelovanje operatora je dovoljno promatrati na bazi (mislim na linearnu kombinaciju), pa uvrštavaš posebno, jedan za drugim, elemente kanonske baze [latex]\{E_{11}, E_{12}, E_{21}, E_{22}\}[/latex]. Trebalo bi se odmah dobiti da je [latex]\alpha=\beta=\gamma=\delta=0[/latex]. Javi ako nešto nije jasno.
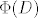 je operator (točnije linearni funkcional je operator (točnije linearni funkcional 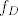 ). Njegova "formula" ti je dana u zadatku. Probaj ne razbijati glavu time kako sve to "izgleda", nego ih promatraj kao i svake druge vektore. ). Njegova "formula" ti je dana u zadatku. Probaj ne razbijati glavu time kako sve to "izgleda", nego ih promatraj kao i svake druge vektore.
Kao što sam napomenuo gore, možeš dokazati da je skup 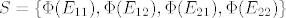 baza za baza za 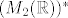 . Dovoljno je pokazati linearnu nezavisnost jer znamo da je . Dovoljno je pokazati linearnu nezavisnost jer znamo da je 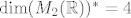 . Uzmeš linearnu kombinaciju tih linearnih funkcionala iz . Uzmeš linearnu kombinaciju tih linearnih funkcionala iz  ( (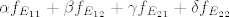 ) i izjednačiš s nulom (tj. pretpostaviš da je nuloperator). No, djelovanje operatora je dovoljno promatrati na bazi (mislim na linearnu kombinaciju), pa uvrštavaš posebno, jedan za drugim, elemente kanonske baze ) i izjednačiš s nulom (tj. pretpostaviš da je nuloperator). No, djelovanje operatora je dovoljno promatrati na bazi (mislim na linearnu kombinaciju), pa uvrštavaš posebno, jedan za drugim, elemente kanonske baze 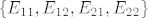 . Trebalo bi se odmah dobiti da je . Trebalo bi se odmah dobiti da je 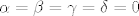 . Javi ako nešto nije jasno. . Javi ako nešto nije jasno.
|
|
| [Vrh] |
|
|








