| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 21:39 pet, 2. 4. 2010 Naslov: zadaci s kolokvija Postano: 21:39 pet, 2. 4. 2010 Naslov: zadaci s kolokvija |
    |
|
|
bio bih jako zahvalan na pomoći sa ovim zadacima ([url=http://web.math.hr/nastava/alg/2008-09/kolokvij200409.pdf]odavde[/url]):
1.) [b]Pokažite da[/b] [latex]\mathbb{Z}_8[/latex][b] i[/b] [latex]\mathbb{Z}_4 \oplus \mathbb{Z}_2[/latex] [b]nisu izomorfne.[/b]
pretpostavljam da trebamo pretpostaviti suprotno, tj. da jesu izomorfne pa definirati neko preslikavanje između [latex]\mathbb{Z}_8=\{ 0, 1,...,7 \}[/latex] i [latex]\mathbb{Z}_4 \oplus \mathbb{Z}_2 =\{ (a,b): a=0,1,2,3; b=0,1,2 \}[/latex] i nekako doći do kontradikcije, no ne znam kako :?
2.) [b]Neka je [latex]G[/latex] grupa i [latex]N \leq G[/latex].
Dokažite da je [latex]N[/latex] normalna ako i samo ako postoji neka grupa [latex]H[/latex] i homomorfizam [latex]f : G \rightarrow H[/latex] takav da je [latex]N = Ker(f)[/latex].[/b]
kako ovo pokazati?
3.) a) [b]Odredite [latex]Int(\mathbb{Z}_9)[/latex] i [latex]Aut(\mathbb{Z}_9)[/latex]. Jesu li te grupe cikličke?[/b]
Novi :wob: je riješio b) dio, ali nigdje nisam u bilježnici našao činjenicu koju koristi u dokazu (da je [latex]Int(G) = \{ id_G\}[/latex]), pa me zanima kako bi se ovaj zadatak mogao riješiti bez toga? a i pretpostavljam da na kolokviju treba svaku tvrdnju obrazložiti pa se dođe na isto.
dakle, zanima me kako "od nule" odredimo što su [latex]Int(\mathbb{Z}_9)[/latex] i [latex]Aut(\mathbb{Z}_9)[/latex], kako, gdje, otkud, zašto :D.
unaprijed zahvaljujem! :D
bio bih jako zahvalan na pomoći sa ovim zadacima (odavde):
1.) Pokažite da 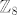 i i  nisu izomorfne. nisu izomorfne.
pretpostavljam da trebamo pretpostaviti suprotno, tj. da jesu izomorfne pa definirati neko preslikavanje između  i i 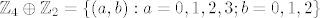 i nekako doći do kontradikcije, no ne znam kako i nekako doći do kontradikcije, no ne znam kako 
2.) Neka je 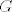 grupa i grupa i  . .
Dokažite da je 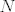 normalna ako i samo ako postoji neka grupa normalna ako i samo ako postoji neka grupa 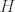 i homomorfizam i homomorfizam  takav da je takav da je  . .
kako ovo pokazati?
3.) a) Odredite 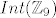 i i  . Jesu li te grupe cikličke? . Jesu li te grupe cikličke?
Novi  je riješio b) dio, ali nigdje nisam u bilježnici našao činjenicu koju koristi u dokazu (da je je riješio b) dio, ali nigdje nisam u bilježnici našao činjenicu koju koristi u dokazu (da je 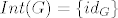 ), pa me zanima kako bi se ovaj zadatak mogao riješiti bez toga? a i pretpostavljam da na kolokviju treba svaku tvrdnju obrazložiti pa se dođe na isto. ), pa me zanima kako bi se ovaj zadatak mogao riješiti bez toga? a i pretpostavljam da na kolokviju treba svaku tvrdnju obrazložiti pa se dođe na isto.
dakle, zanima me kako "od nule" odredimo što su 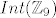 i i  , kako, gdje, otkud, zašto , kako, gdje, otkud, zašto  . .
unaprijed zahvaljujem! 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 2:12 sub, 3. 4. 2010 Naslov: Postano: 2:12 sub, 3. 4. 2010 Naslov: |
    |
|
|
[b]Lema.[/b] Neka je [latex]G[/latex] Abelova grupa s jedinicom [latex]e[/latex], tada je [latex]\mathrm{Int}{\left(G\right)} = \left\{\mathrm{id}_G\right\}[/latex].
[b]Dokaz.[/b] Neka je [latex]g \in G[/latex] proizvoljan, pokažimo da je [latex]I_g \equiv \mathrm{id}_G[/latex]. Za svaki [latex]x \in G[/latex] vrijedi da je [latex]I_g\left(x\right) = g x g^{-1} =[/latex] (pošto je grupa Abelova) [latex]= g g^{-1} x = ex = x = \mathrm{id}_G\left(x\right)[/latex]. Ovime je lema dokazana.
Sada je jasno da je [latex]\mathrm{Int}{\mathbb{Z}_9} = \left\{\mathrm{id}_{\mathbb{Z}_9}\right\}[/latex], naime, [latex]\mathbb{Z}_9[/latex] je ciklička grupa, a iz toga odmah slijedi da je Abelova.
Što se tiče [latex]\mathrm{Aut}{\left(\mathbb{Z}_9\right)}[/latex], svaki automorfizam je posebno endomorfizam (homomorfizam sa skupa na samoga sebe), pošto je grupa [latex]\mathbb{Z}_9[/latex] ciklička svaki endomorfizam na njoj je određen djelovanjem na generator (npr. na [latex]1[/latex]).
Da bi dobiveni endomorfizam bio automorfizam jasno je da on generator mora preslikati na generator. Svi endomorfizmi na [latex]\mathbb{Z}_9[/latex] dani su sa
[latex]\mathrm{End}{\left(\mathbb{Z}_9\right)} = \left\{f_i : \mathbb{Z}_9 \to \mathbb{Z}_9,\ f_i\left(1\right) = i,\ i=0,\, 1,\, \ldots,\, 8 \right\}[/latex] (znači, ima ih [latex]9[/latex], jer ima [latex]9[/latex] mogućnosti kamo preslikati jedinicu).
Sada, tražimo automorfizme, to su endomorfizmi koji su bijekcije. Znamo da je generator cikličke grupe [latex]G[/latex] svaki element [latex]g \in G[/latex] za koji vrijedi da su brojevi [latex]\left|g\right|[/latex] i [latex]\left|G\right|[/latex] jednaki (Svaki takav element i samo takvi elementi!).
Dakle, vrijedi
[latex]\mathrm{Aut}{\left(\mathbb{Z}_9\right)} = \left\{f_1,\, f_2,\, f_4,\, f_5,\, f_7,\, f_8\right\}[/latex].
Vidimo da je
[latex]f_2 \circ f_2 = f_4[/latex],
[latex]f_4 \circ f_2 = f_8[/latex],
[latex]f_8 \circ f_2 = f_7[/latex],
[latex]f_7 \circ f_2 = f_5[/latex],
[latex]f_5 \circ f_2 = f_1[/latex].
Dakle, [latex]\left|f_2\right| = 6 = \left|\mathrm{Aut}{\left(\mathbb{Z}_9\right)}\right|[/latex], pa je [latex]\mathrm{Aut}{\left(\mathbb{Z}_9\right)}[/latex] ciklička ([latex]f_2[/latex] je generator), konačno, izomorfna je sa [latex]\mathbb{Z}_6[/latex] (kao i svaka druga ciklička grupa reda [latex]6[/latex]).
Lema. Neka je 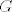 Abelova grupa s jedinicom Abelova grupa s jedinicom  , tada je , tada je  . .
Dokaz. Neka je  proizvoljan, pokažimo da je proizvoljan, pokažimo da je 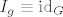 . Za svaki . Za svaki 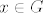 vrijedi da je vrijedi da je 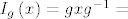 (pošto je grupa Abelova) (pošto je grupa Abelova) 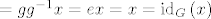 . Ovime je lema dokazana. . Ovime je lema dokazana.
Sada je jasno da je 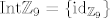 , naime, , naime,  je ciklička grupa, a iz toga odmah slijedi da je Abelova. je ciklička grupa, a iz toga odmah slijedi da je Abelova.
Što se tiče 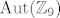 , svaki automorfizam je posebno endomorfizam (homomorfizam sa skupa na samoga sebe), pošto je grupa , svaki automorfizam je posebno endomorfizam (homomorfizam sa skupa na samoga sebe), pošto je grupa  ciklička svaki endomorfizam na njoj je određen djelovanjem na generator (npr. na ciklička svaki endomorfizam na njoj je određen djelovanjem na generator (npr. na  ). ).
Da bi dobiveni endomorfizam bio automorfizam jasno je da on generator mora preslikati na generator. Svi endomorfizmi na  dani su sa dani su sa
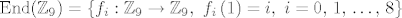 (znači, ima ih (znači, ima ih  , jer ima , jer ima  mogućnosti kamo preslikati jedinicu). mogućnosti kamo preslikati jedinicu).
Sada, tražimo automorfizme, to su endomorfizmi koji su bijekcije. Znamo da je generator cikličke grupe 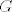 svaki element svaki element  za koji vrijedi da su brojevi za koji vrijedi da su brojevi 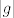 i i  jednaki (Svaki takav element i samo takvi elementi!). jednaki (Svaki takav element i samo takvi elementi!).
Dakle, vrijedi
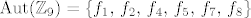 . .
Vidimo da je
 , ,
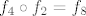 , ,
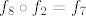 , ,
 , ,
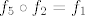 . .
Dakle, 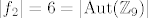 , pa je , pa je 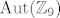 ciklička ( ciklička (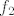 je generator), konačno, izomorfna je sa je generator), konačno, izomorfna je sa  (kao i svaka druga ciklička grupa reda (kao i svaka druga ciklička grupa reda  ). ).
Zadnja promjena: JANKRI; 21:20 sub, 3. 4. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 7:46 sub, 3. 4. 2010 Naslov: Re: zadaci s kolokvija Postano: 7:46 sub, 3. 4. 2010 Naslov: Re: zadaci s kolokvija |
    |
|
|
puno hvala, Braslav i JANKRI!
[quote="Braslav"]Ako je [latex]N=Ker(f)[/latex] onda je [latex]N[/latex] normalna, a obrnuto promatramo kanonski epimorfizam koji salje element [latex]g[/latex] od [latex]G[/latex] u klasu [latex]gN[/latex] tada je jezgra tog epimorfizma tocno [latex]N[/latex].[/quote]
jasan mi je ovaj smjer:
imamo grupu [latex]G[/latex] i ako je [latex]N[/latex] njena normalna podgrupa, onda zaista postoji neka grupa [latex]H := G/_{N}[/latex] i neki homomorfizam [latex]f:G \rightarrow H[/latex], pri čemu je [latex]f:=\pi_N[/latex] kanonski epimorfizam i po Teoremu 1.27 (str.18 [url=http://web.math.hr/nastava/alg/predavanja/ASpred.pdf]ovdje[/url]) je [latex]N = Ker(f)[/latex].
sad me zanima kako pokazati drugi smjer, odnosno
[quote="Braslav"]Ako je [latex]N=Ker(f)[/latex] onda je [latex]N[/latex] normalna[/quote] uz pretpostavke iz zadatka?
puno hvala, Braslav i JANKRI!
| Braslav (napisa): | Ako je  onda je onda je 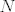 normalna, a obrnuto promatramo kanonski epimorfizam koji salje element normalna, a obrnuto promatramo kanonski epimorfizam koji salje element  od od 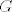 u klasu u klasu 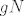 tada je jezgra tog epimorfizma tocno tada je jezgra tog epimorfizma tocno 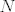 . . |
jasan mi je ovaj smjer:
imamo grupu 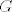 i ako je i ako je 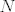 njena normalna podgrupa, onda zaista postoji neka grupa njena normalna podgrupa, onda zaista postoji neka grupa  i neki homomorfizam i neki homomorfizam 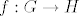 , pri čemu je , pri čemu je 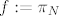 kanonski epimorfizam i po Teoremu 1.27 (str.18 ovdje) je kanonski epimorfizam i po Teoremu 1.27 (str.18 ovdje) je  . .
sad me zanima kako pokazati drugi smjer, odnosno
| Braslav (napisa): | Ako je  onda je onda je 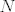 normalna normalna |
uz pretpostavke iz zadatka?
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 8:36 sub, 3. 4. 2010 Naslov: Postano: 8:36 sub, 3. 4. 2010 Naslov: |
    |
|
|
Neka su [latex]G[/latex] i [latex]H[/latex] grupe i [latex]f : G \to H[/latex] homomorfizam takav da je [latex]\mathrm{Ker}{\left(f\right)}=N[/latex].
Želimo pokazati da je [latex]N \trianglelefteq G[/latex].
Pokažimo najprije da je [latex]N \leq G[/latex], neka su [latex]x,\, y \in N[/latex], vrijedi [latex]f\left(xy\right)=f\left(x\right)f\left(y\right)=ee=e[/latex], dalje [latex]f\left(x^{-1}\right)=f\left(x\right)^{-1}=e^{-1}=e[/latex]. Dakle, [latex]N \leq G[/latex].
Dalje, neka je [latex]g \in G[/latex] i [latex]n \in N[/latex], tada je
[latex]f\left(g n g^{-1}\right)=f\left(g\right) f\left(n\right) f\left(g^{-1}\right) = f\left(g\right) e f\left(g\right)^{-1} = e[/latex]. Dakle, [latex]g n g^{-1} \in N[/latex], pa je [latex]N \trianglelefteq G[/latex].
Neka su 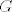 i i 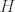 grupe i grupe i 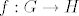 homomorfizam takav da je homomorfizam takav da je 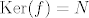 . .
Želimo pokazati da je 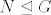 . .
Pokažimo najprije da je  , neka su , neka su 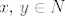 , vrijedi , vrijedi 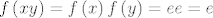 , dalje , dalje 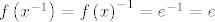 . Dakle, . Dakle,  . .
Dalje, neka je  i i 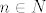 , tada je , tada je
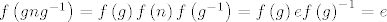 . Dakle, . Dakle, 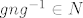 , pa je , pa je 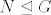 . .
|
|
| [Vrh] |
|
jejo
Forumaš(ica)

Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
jejo
Forumaš(ica)


Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
tm
Forumaš(ica)
Pridružen/a: 07. 12. 2007. (20:17:52)
Postovi: (39)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
maxic
Forumaš(ica)
Pridružen/a: 10. 02. 2009. (20:11:13)
Postovi: (45)16
|
 Postano: 10:02 sri, 14. 4. 2010 Naslov: Postano: 10:02 sri, 14. 4. 2010 Naslov: |
    |
|
|
Možda niste znali, ali smo za kolokvij iz Računarskog praktikuma podijeljeni u tri grupe, pa tako prva grupa piše u 9:00, druga u 11:15 i treća u 13:30. Očito kolege iz druge grupe nikako neće moći biti prisutni na žalbama. Osim toga, dosta ljudi sluša kolegij Programiranje 2 čiji kolokvij je upravo u 12. Da li bi se žalbe mogle prebaciti recimo u 11:00 ili čak u 10:45 tako da su svi u mogućnosti doći na žalbe.
Btw, drago mi je vidjeti da se išlo staviti žalbe u vrijeme kada se očekivalo da bi većina trebala biti na faksu ili u blizini, a ne u dane kada inače nitko ne bi došao na faks, što je često bila praksa iz nekih kolegija. Hvala!!
Možda niste znali, ali smo za kolokvij iz Računarskog praktikuma podijeljeni u tri grupe, pa tako prva grupa piše u 9:00, druga u 11:15 i treća u 13:30. Očito kolege iz druge grupe nikako neće moći biti prisutni na žalbama. Osim toga, dosta ljudi sluša kolegij Programiranje 2 čiji kolokvij je upravo u 12. Da li bi se žalbe mogle prebaciti recimo u 11:00 ili čak u 10:45 tako da su svi u mogućnosti doći na žalbe.
Btw, drago mi je vidjeti da se išlo staviti žalbe u vrijeme kada se očekivalo da bi većina trebala biti na faksu ili u blizini, a ne u dane kada inače nitko ne bi došao na faks, što je često bila praksa iz nekih kolegija. Hvala!!
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
jejo
Forumaš(ica)


Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
maxic
Forumaš(ica)
Pridružen/a: 10. 02. 2009. (20:11:13)
Postovi: (45)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:03 sri, 14. 4. 2010 Naslov: Postano: 18:03 sri, 14. 4. 2010 Naslov: |
    |
|
|
[quote="jejo"]Jel bi mogli ikako prije objaviti rezultate, tako da ne budu u isto vrijeme kao i zalbe, tipa sat, dva ranije, tako da oni koji bi bili zadovoljni bodovima ne moraju bezveze dolaziti na fax?[/quote]
S obzirom na to da će rezultate objaviti danas, a žalbe su sutra, ne kužim u čemu je problem.
Btw, svaka pohvala za to, živim dosta daleko od faksa i stvarno me ubije u pojam kad su žalbe odmah nakon objave rezultata (što najčešće jesu :-/) jer izgubim 3-4 sata na put tamo i nazad tako da HVALA još jednom :-)))
| jejo (napisa): | | Jel bi mogli ikako prije objaviti rezultate, tako da ne budu u isto vrijeme kao i zalbe, tipa sat, dva ranije, tako da oni koji bi bili zadovoljni bodovima ne moraju bezveze dolaziti na fax? |
S obzirom na to da će rezultate objaviti danas, a žalbe su sutra, ne kužim u čemu je problem.
Btw, svaka pohvala za to, živim dosta daleko od faksa i stvarno me ubije u pojam kad su žalbe odmah nakon objave rezultata (što najčešće jesu :-/) jer izgubim 3-4 sata na put tamo i nazad tako da HVALA još jednom  )) ))
|
|
| [Vrh] |
|
jejo
Forumaš(ica)


Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
matovillka
Forumaš(ica)
Pridružen/a: 27. 03. 2009. (20:47:50)
Postovi: (3E)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
















