| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
 Postano: 11:47 ned, 28. 2. 2010 Naslov: Fubinijev teorem Postano: 11:47 ned, 28. 2. 2010 Naslov: Fubinijev teorem |
    |
|
|
u [url=http://web.math.hr/nastava/difraf/int/pred/p_o5.pdf]dokazu Fubinijevog teorema[/url] pred kraj (str. 9) želimo pokazati
[latex]\int_A f = \int_a^b g(x)dx[/latex]
koristimo (5.1) [latex]s_f(P) \leq s_g(P_{[a,b]}) \leq S_g(P_{[a,b]}) \leq S_f(P)[/latex]
Za proizvoljnu particiju [latex]P=(P_{[a,b]},P_{[c,d]})[/latex],
[latex]S_g(P_{[a,b]})[/latex] će biti jedna gornja Darbouxova suma od [latex]g[/latex]. kako je [latex]I^*(g)[/latex] infimum svih gornjih Darbouxovih suma, jasno mi je da vrijedi (prema (5.1))
[latex]I^*(g) \leq S_g(P_{[a,b]}) \leq S_f(P)[/latex]
odnosno, (5.1) možemo proširiti kao
[latex]s_f(P) \leq s_g(P_{[a,b]})\leq I_*(g) \leq I^*(g) \leq S_g(P_{[a,b]}) \leq S_f(P)[/latex][color=white]......[/color](5.1a)
E sad, moje je pitanje: zašto vrijedi [latex]I^*(f) \geq I^*(g)[/latex] i otkud to slijedi? Ako je [latex]I^*(f)[/latex] veće od [latex]I^*(g)[/latex], gdje (tj. između kojih članova) bi ga se moglo ubaciti u (5.1a)?
Puno hvala na pomoći! :zlatnizub:
u dokazu Fubinijevog teorema pred kraj (str. 9) želimo pokazati
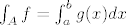
koristimo (5.1) 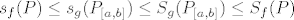
Za proizvoljnu particiju 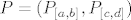 , ,
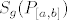 će biti jedna gornja Darbouxova suma od će biti jedna gornja Darbouxova suma od  . kako je . kako je 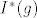 infimum svih gornjih Darbouxovih suma, jasno mi je da vrijedi (prema (5.1)) infimum svih gornjih Darbouxovih suma, jasno mi je da vrijedi (prema (5.1))
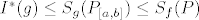
odnosno, (5.1) možemo proširiti kao
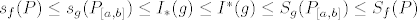 ......(5.1a) ......(5.1a)
E sad, moje je pitanje: zašto vrijedi 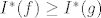 i otkud to slijedi? Ako je i otkud to slijedi? Ako je 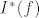 veće od veće od 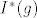 , gdje (tj. između kojih članova) bi ga se moglo ubaciti u (5.1a)? , gdje (tj. između kojih članova) bi ga se moglo ubaciti u (5.1a)?
Puno hvala na pomoći! 
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
piko
Forumaš(ica)


Pridružen/a: 09. 10. 2009. (18:20:25)
Postovi: (26)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
|






