| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
 Postano: 20:50 sri, 13. 2. 2008 Naslov: Zadatak s prošlogodišnjeg kolokvija (2007) Postano: 20:50 sri, 13. 2. 2008 Naslov: Zadatak s prošlogodišnjeg kolokvija (2007) |
    |
|
|
Lijen sam pisati :lol:
[img]http://img100.imageshack.us/img100/3692/zadatakmq4.jpg[/img]
Isti zadatak je bio i za drugu grupu, samo drugačije formuliran.
Dakle, kako se to dokazuje? Očito je da su r(M) i r(N) oboje 1, no nekako mi se čini prelako da bi riješenje bilo r(MN)=r(M)*r(N) ili =min[r(M);r(N)]. Help! :oops:
Obrat mi se čini još i teži, pa ako bi netko htio rasvijetliti ovaj problem, bio bih zahvalan! :D
Lijen sam pisati 

Isti zadatak je bio i za drugu grupu, samo drugačije formuliran.
Dakle, kako se to dokazuje? Očito je da su r(M) i r(N) oboje 1, no nekako mi se čini prelako da bi riješenje bilo r(MN)=r(M)*r(N) ili =min[r(M);r(N)]. Help! 
Obrat mi se čini još i teži, pa ako bi netko htio rasvijetliti ovaj problem, bio bih zahvalan! 
_________________
Cry havoc, and let loose the dogs of war!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
 Postano: 21:21 sri, 13. 2. 2008 Naslov: Postano: 21:21 sri, 13. 2. 2008 Naslov: |
    |
|
|
OK, shvaćam prvi smjer, svi retci matrice MN su međusobno linearno zavisni (jer su svi zapravo linearne kombinacije jednoretčane matrice N) te je očito rang 1.
No još uvijek ne razumijem u potpunosti obratni smijer.
Ako je rang 1, onda su retci međusobno zavisni, dakle elementarnim transformacijama nad retcima može se dobiti ekvivalentna matrica u kojoj su svi retci osim prvog jednaki nuli. Onda je očito da je matrica N upravo taj prvi redak, a matrica M je onda e_1, tj. prvi element je 1, svi ostali 0.
Jel to dobro? :)
OK, shvaćam prvi smjer, svi retci matrice MN su međusobno linearno zavisni (jer su svi zapravo linearne kombinacije jednoretčane matrice N) te je očito rang 1.
No još uvijek ne razumijem u potpunosti obratni smijer.
Ako je rang 1, onda su retci međusobno zavisni, dakle elementarnim transformacijama nad retcima može se dobiti ekvivalentna matrica u kojoj su svi retci osim prvog jednaki nuli. Onda je očito da je matrica N upravo taj prvi redak, a matrica M je onda e_1, tj. prvi element je 1, svi ostali 0.
Jel to dobro? 
_________________
Cry havoc, and let loose the dogs of war!
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:41 sri, 13. 2. 2008 Naslov: Postano: 21:41 sri, 13. 2. 2008 Naslov: |
    |
|
|
[latex]
A \sim D_{1}=\left ( \begin{array}{ccc} 1 & 0 & \dots \ 0 \\0 & 0 & \dots \ 0 \\ \vdots & \vdots & \ddots \ \ \vdots \\ 0 & 0 & \dots \ 0 \end{array} \right)=\left ( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right) \left ( \begin{array}{ccc} 1 & 0 & \dots \ 0 \end{array} \right )
[/latex]
pa postoje elementarne matrice [latex]
E_{1},E_{2} , ... , E_{k}, \ F_{1},F_{2},...,F_{l} \ \in M_{n,n}
[/latex] td [latex]
A=E_{1}E_{2}...E_{k}D_{1}F_{1}F_{2}...F_{l}=E_{1}E_{2}...E_{k}\left ( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right) \left ( \begin{array}{ccc} 1 & 0 & \dots \ 0 \end{array} \right )F_{1}F_{2}...F_{l}.
[/latex]
[latex]
B:= E_{1}E_{2}...E_{k}\left ( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right) \in M_{n,1}, \ \ C:= \left ( \begin{array}{ccc} 1 & 0 & \dots \ 0 \end{array} \right )F_{1}F_{2}...F_{l} \in M_{1,n}
[/latex].
Traženi formati su očiti, i jasno da su B i C ne-nul matrice, te A=BC.
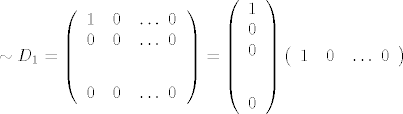
pa postoje elementarne matrice 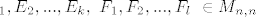 td td 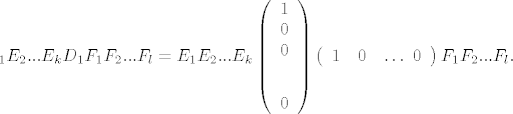
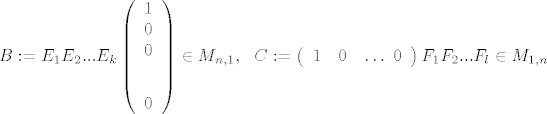 . .
Traženi formati su očiti, i jasno da su B i C ne-nul matrice, te A=BC.
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|








