| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 12:40 pet, 1. 10. 2010 Naslov: Pomoć oko zadataka... Postano: 12:40 pet, 1. 10. 2010 Naslov: Pomoć oko zadataka... |
    |
|
|
1. Zadana mi je f-ja f(x)=|x^2+6x+8|-|x^2+4x+3|. Treba odredit f^-1(<1,2]). I ugl. cijelo vrijeme mi ispada krivi rezultat,a ne znam zasto...posto se iz grafa ne moze vidjet rezultat mora se racunski odrediti pa imamo da 1<f(x)<=2 . I vjerojatno grjesim negdje kad micem apsolutno. Pa ako itko ima vremena da mi napise samo pocetni korak, da vidim gdje grijesim (Rj: <(-5-sqrt5)/2, (-5+sqrt5)/2.
2. Zadana je f-ja f(x)=cos^4+sin^4, odredite f^-1(<0,5/8>). I prvo pojednostavim ovu f-ju tako da mi f(x)=cos^2(2x). I sad, ne znam dal mi rješenje ispada točno.. [(3pi/4)+2k(pi),pi+2k(pi)>U<2(pi)+2k(pi),(pi/4)+2k(pi)],k je iz Z. Pa ako netko ima volje rjesavat ovakav zadatak, neka mi javi rezultat.
HVALA UNAPRIJED!! 8)
1. Zadana mi je f-ja f(x)=|x^2+6x+8|-|x^2+4x+3|. Treba odredit f^-1(<1,2]). I ugl. cijelo vrijeme mi ispada krivi rezultat,a ne znam zasto...posto se iz grafa ne moze vidjet rezultat mora se racunski odrediti pa imamo da 1<f(x)⇐2 . I vjerojatno grjesim negdje kad micem apsolutno. Pa ako itko ima vremena da mi napise samo pocetni korak, da vidim gdje grijesim (Rj: <(-5-sqrt5)/2, (-5+sqrt5)/2.
2. Zadana je f-ja f(x)=cos^4+sin^4, odredite f^-1(<0,5/8>). I prvo pojednostavim ovu f-ju tako da mi f(x)=cos^2(2x). I sad, ne znam dal mi rješenje ispada točno.. [(3pi/4)+2k(pi),pi+2k(pi)>U<2(pi)+2k(pi),(pi/4)+2k(pi)],k je iz Z. Pa ako netko ima volje rjesavat ovakav zadatak, neka mi javi rezultat.
HVALA UNAPRIJED!! 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:56 pet, 1. 10. 2010 Naslov: Postano: 15:56 pet, 1. 10. 2010 Naslov: |
    |
|
|
Ah, nova sezona. :D
Dakle, u prvom zadatku početni korak bi bio da faktoriziraš kvadratne funkcije [latex]x^2+6x+8=(x+2)(x+4)[/latex] i [latex]x^2+4x+3=(x+1)(x+3)[/latex]. Nakon toga gledaj po slučajevima o kojima ovisi pozitivnost tih kvadratnih funkcija. Tako mi se čini da ćeš se najlakše riješiti apsolutnih vrijednosti. Dakle, slučajevi bi bili [latex]x<-4[/latex], [latex]-4\leq x<-3[/latex], [latex]-3\leq x<-2[/latex], [latex]-2\leq x<-1[/latex] i [latex]-1\leq x[/latex]. Nakon toga ćeš u nekim slučajevima dobiti novu kvadratnu funkciju, a u nekima linearnu, a nakon toga možeš ići računski ili probati čitati s grafa, što bi se ipak u određenoj mjeri vjerojatno moralo moći - [url=http://www.wolframalpha.com/input/?i=|x^2%2B6x%2B8|-|x^2%2B4x%2B3|]stvar[/url] i nije toliko odvratna. :) Na WolframAlphi možeš i saznati koja su rješenja, ali nije baš uvijek najintuitivnija, tako da ponekad treba malo preformulirati stvar. Rekao si da hoćeš samo prvi korak, pa ne želim pokvariti zabavu. :D Reci ako treba napisati i rješenja. Mislim da sam nekoć prošle godine komentirao taj ili neki vrlo sličan zadatak negdje na forumu, pa slobodno potraži ako nešto nije jasno.
U drugom zadatku ne znam baš kako si uspio doći do toga da je [latex]f(x)=\cos^2(2x)[/latex]. Meni ispada [latex]f(x)=\cos^4 x+\sin^4 x=(\cos^2 x+\sin^2 x)- 2\sin^2 x\cos^2 x=1-2\sin^2 x\cos^2 x[/latex]. Budući da je [latex]4\sin^2 x\cos^2 x=\sin^2 (2x)[/latex], imamo [latex]f(x)=1-\displaystyle\frac{\sin^2 (2x)}{2}[/latex], a to nije [latex]\cos^2 (2x)[/latex]. Najljepše što mogu dobiti mi ispada [latex]f(x)=1-\displaystyle\frac{1-\cos (4x)}{4}=\displaystyle\frac{\cos(4x)+3}{4}[/latex].
Onda tvoj problem i nije toliko težak: traži se, zapravo, [latex]-\displaystyle\frac{1}{2}>\cos(4x)>-3[/latex] (pri čemu druga nejednakost zapravo uvijek vrijedi, pa nam i ne igra neku ulogu), pa je [latex]4x\in\displaystyle\bigcup_{k\in\mathbb{Z}}\langle\displaystyle\frac{2\pi}{3}+2k\pi,\displaystyle\frac{4\pi}{3}+2k\pi\rangle[/latex]. Dakle, [latex]x\in\displaystyle\bigcup_{k\in\mathbb{Z}}\langle\displaystyle\frac{\pi}{6}+\displaystyle\frac{k\pi}{2},\displaystyle\frac{\pi}{3}+\displaystyle\frac{k\pi}{2}\rangle[/latex] bi trebao biti skup rješenja.
Tu sam gore na mjestima malo brz, ali nadam se da je sve barem relativno točno. :)
Ah, nova sezona. 
Dakle, u prvom zadatku početni korak bi bio da faktoriziraš kvadratne funkcije 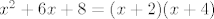 i i 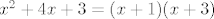 . Nakon toga gledaj po slučajevima o kojima ovisi pozitivnost tih kvadratnih funkcija. Tako mi se čini da ćeš se najlakše riješiti apsolutnih vrijednosti. Dakle, slučajevi bi bili . Nakon toga gledaj po slučajevima o kojima ovisi pozitivnost tih kvadratnih funkcija. Tako mi se čini da ćeš se najlakše riješiti apsolutnih vrijednosti. Dakle, slučajevi bi bili 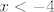 , ,  , , 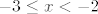 , , 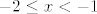 i i  . Nakon toga ćeš u nekim slučajevima dobiti novu kvadratnu funkciju, a u nekima linearnu, a nakon toga možeš ići računski ili probati čitati s grafa, što bi se ipak u određenoj mjeri vjerojatno moralo moći - stvar i nije toliko odvratna. . Nakon toga ćeš u nekim slučajevima dobiti novu kvadratnu funkciju, a u nekima linearnu, a nakon toga možeš ići računski ili probati čitati s grafa, što bi se ipak u određenoj mjeri vjerojatno moralo moći - stvar i nije toliko odvratna.  Na WolframAlphi možeš i saznati koja su rješenja, ali nije baš uvijek najintuitivnija, tako da ponekad treba malo preformulirati stvar. Rekao si da hoćeš samo prvi korak, pa ne želim pokvariti zabavu. Na WolframAlphi možeš i saznati koja su rješenja, ali nije baš uvijek najintuitivnija, tako da ponekad treba malo preformulirati stvar. Rekao si da hoćeš samo prvi korak, pa ne želim pokvariti zabavu.  Reci ako treba napisati i rješenja. Mislim da sam nekoć prošle godine komentirao taj ili neki vrlo sličan zadatak negdje na forumu, pa slobodno potraži ako nešto nije jasno. Reci ako treba napisati i rješenja. Mislim da sam nekoć prošle godine komentirao taj ili neki vrlo sličan zadatak negdje na forumu, pa slobodno potraži ako nešto nije jasno.
U drugom zadatku ne znam baš kako si uspio doći do toga da je 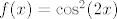 . Meni ispada . Meni ispada 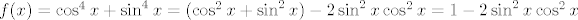 . Budući da je . Budući da je 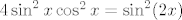 , imamo , imamo 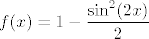 , a to nije , a to nije 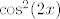 . Najljepše što mogu dobiti mi ispada . Najljepše što mogu dobiti mi ispada 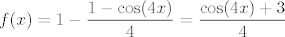 . .
Onda tvoj problem i nije toliko težak: traži se, zapravo, 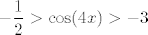 (pri čemu druga nejednakost zapravo uvijek vrijedi, pa nam i ne igra neku ulogu), pa je (pri čemu druga nejednakost zapravo uvijek vrijedi, pa nam i ne igra neku ulogu), pa je 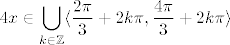 . Dakle, . Dakle, 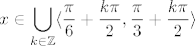 bi trebao biti skup rješenja. bi trebao biti skup rješenja.
Tu sam gore na mjestima malo brz, ali nadam se da je sve barem relativno točno. 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
|




