| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 13:49 čet, 13. 5. 2010 Naslov: Re: Skalarni produkt - pomoc oko zadatka Postano: 13:49 čet, 13. 5. 2010 Naslov: Re: Skalarni produkt - pomoc oko zadatka |
    |
|
|
[quote="CROmpir"]1. kako definirati skalarni produkt u v2 i v1? Kako tada glasi zapis preko koordinata vektora.[/quote]
Vjerojatno misliš na [latex]V^2[/latex] i [latex]V^3[/latex]. Kakogod, skalarni produkt [latex]\cdot : V^2 \times V^2 \to \mathbb{R}[/latex], odnosno [latex]\cdot : V^3 \times V^3 \to \mathbb{R}[/latex] se definira s [latex]\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \angle (\vec{a}, \vec{b})[/latex] za netrivijalne vektore, a inače 0.
Ako je [latex]\vec{a} = a_1 \vec{i} + a_2 \vec{j} + a_3 \vec{k}[/latex] i [latex]\vec{b} = b_1 \vec{i} + b_2 \vec{j} + b_3 \vec{k}[/latex], koristeći svojstva skalarnog produkta se lako dobi da je [latex]\vec{a} \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3[/latex].
[quote="CROmpir"]2. Neka su a i b vektori za koje je |a|=1, |b|=3 i <(a,b)=pi/3. Izracunajte skalarni produkt vektora a+3b i 2a-b... (moze li mi netko objasniti po koracima kako? )..[/quote]
To je jednostavno, jer za skalarni produkt vrijede lijepa svojstva (komutativnost, distributivnost, kvaziasocijativnost,...). Odmah se dobije da je [latex](\vec{a}+3 \vec{b})(2 \vec{a}-\vec{b}) = 2 \vec{a}^2 + 5 \vec{a} \vec{b} - 3 \vec{b}^2[/latex]. Korištenjem definicije skalarnog produkta, dobivamo da je to jednako -35/2.
| CROmpir (napisa): | | 1. kako definirati skalarni produkt u v2 i v1? Kako tada glasi zapis preko koordinata vektora. |
Vjerojatno misliš na 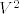 i i 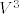 . Kakogod, skalarni produkt . Kakogod, skalarni produkt 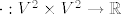 , odnosno , odnosno 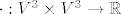 se definira s se definira s 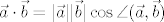 za netrivijalne vektore, a inače 0. za netrivijalne vektore, a inače 0.
Ako je 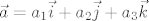 i i 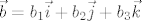 , koristeći svojstva skalarnog produkta se lako dobi da je , koristeći svojstva skalarnog produkta se lako dobi da je 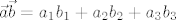 . .
| CROmpir (napisa): | | 2. Neka su a i b vektori za koje je |a|=1, |b|=3 i <(a,b)=pi/3. Izracunajte skalarni produkt vektora a+3b i 2a-b... (moze li mi netko objasniti po koracima kako? ).. |
To je jednostavno, jer za skalarni produkt vrijede lijepa svojstva (komutativnost, distributivnost, kvaziasocijativnost,...). Odmah se dobije da je 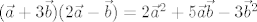 . Korištenjem definicije skalarnog produkta, dobivamo da je to jednako -35/2. . Korištenjem definicije skalarnog produkta, dobivamo da je to jednako -35/2.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
|





