|
Evo, kolega [url=http://degiorgi.math.hr/forum/profile.php?mode=viewprofile&u=3102]Gino[/url] i ja (velikom većinom on :D) smo ipak uspjeli rješiti, pa ako nekoga zanima... :)
Dakle, želimo pokazati da je [latex]\det{\left(\nabla{F}^{\tau}\nabla{F}\right)} = 1 + \left|\nabla{f}\right|^2[/latex].
Vrijedi [latex] \nabla{F} = \left[\begin{array}{cccc}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
0 & 0 & \cdots & 0 \\
\cdots & \cdots & \cdots & \cdots \\
\frac{\partial{f}}{\partial{x_1}} & \frac{\partial{f}}{\partial{x_2}} & \cdots & \frac{\partial{f}}{\partial{x_{n-1}}}
\end{array}\right]
[/latex]. [size=1]zašto ne radi \vdots?[/size]
Sada koristimo Binet - Cauchyjevu produktnu formulu, iz koje slijedi:
[latex]\det{\left(\nabla{F}^{\tau}\nabla{F}\right)} = \sum\limits_{\left[I\right]}{\det{\nabla{F}_I}\det{\nabla{F}_I}}=\sum\limits_{\left[I\right]}{\left(\det{\nabla{F}_I\right)^2}[/latex]. Ovjde nam [latex]\left[I\right][/latex] označava da sumiramo po rastućim [latex]\left(n-1\right)[/latex]-torkama iz skupa [latex]\left\{1,\, 2,\, \ldots,\, n\right\}[/latex], dok nam [latex]\nabla{F}_I[/latex] označava [latex]\left(n-1\right) \times \left(n-1\right)[/latex] matricu dobivenu iz matrice [latex]\nabla{F}[/latex] tako da joj je [latex]k[/latex]-ti redak jednak [latex]i_k[/latex]-tom retku matrice [latex]\nabla{F}[/latex], [latex]k=1,\,2,\, \ldots,\, n-1[/latex], [latex]i_k \in I[/latex]. (Odnosno, dobivena je tako da iz matrice [latex]\nabla{F}[/latex] izbacimo onaj redak čiji se redni broj ne pojavljuje u [latex]\left(n-1\right)[/latex]-torci [latex]I[/latex].) Jasno je da rastućih [latex]\left(n-1\right)[/latex]-torki postoji točno [latex]n[/latex], naime, koji god broj da izbacimo iz skupa [latex]\left\{1,\, 2,\, \ldtos,\, n\right\}[/latex] dobijemo jednu (točno jednu!) takvu [latex]\left(n-1\right)[/latex]-torku.
Izračunajmo najprije koliko je [latex]\left(\det{\nabla{F}_{\left(1,\, 2,\, \ldots,\, n-1\right)}}\right)^2[/latex].
Očito je [latex]\nabla{F}_{\left(1,\, 2,\, \ldots,\, n-1\right)} = \left[\begin{array}{ccccc}
1 & 0 & 0 & \cdots & 0 \\
0 & 1 & 0 & \cdots & 0 \\
0 & 0 & 1 & \cdots & 0 \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
0 & 0 & 0 & \cdots & 1
\end{array}\right][/latex], stoga je [latex]\left(\det{\nabla{F}_{\left(1,\, 2,\, \ldots,\, n-1\right)}}\right)^2=1^2=1[/latex].
Dalje, za svaku ostalu rastuću [latex]\left(n-1\right)[/latex]-torku jasno je da ćemo "uzeti" [latex]n[/latex]-ti redak, a nećemo "uzeti" jedan od prvih [latex]n-1[/latex], neka je [latex]I[/latex] jedna takva rastuća [latex]\left(n-1\right)[/latex]-torka i neka je [latex]i \in \left\{1,\, 2,\, \ldots,\, n-1\right\}[/latex] onaj kojeg nismo uzeli. Promotrimo sada [latex]\left(i-1\right)[/latex]-vi (kada je [latex]i=1[/latex] postupamo isto kao što ćemo sada objasniti, pa ne treba taj slučaj posebno razmatrati, isto u slučaju [latex]i=n-1[/latex]) i [latex]\left(i+1\right)[/latex]-vi redak matrice [latex]\nabla{F}[/latex], oni su redom [latex]\left(i-1\right)[/latex]-vi i [latex]i[/latex]-ti redak matrice [latex]\nabla{F}_I[/latex].
[latex]\left[\begin{array}{ccccccc}
\cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\
0 & \cdots & 1 & 0 & 0 & \cdots & 0 \\
0 & \cdots & 0 & 0 & 1 & \cdots & 0 \\
\cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots
\end{array}\right][/latex]
U svakom retku (osim u zadnjem) matrice [latex]\nabla{F}_I[/latex] nalazi se jedna i samo jedna [latex]1[/latex], a ostalo su [latex]0[/latex]. Sada se sjetimo definicije determinante, jedini ne-nul sumand će biti onaj kada u svakom retku osim u zadnjem uzmemo tu jednu jedinicu, što će reći da iz zadnjeg retka moramo uzeti element koji se nalazi u [latex]i[/latex]-tom stupcu. Dakle,
[latex]\left(\det{\nabla{F}_I}\right)^2=\left(\pm\frac{\partial{f}}{\partial{x_i}}\right)^2=\left(\frac{\partial{f}}{\partial{x_i}}\right)^2[/latex].
Konačno,
[latex]\det{\left(\nabla{F}^{\tau}\nabla{F}\right)}=\sum\limits_{\left[I\right]}{\left(\det{\nabla{F}_I\right)^2} = 1 + \sum\limits_{i=1}^{n-1}{\left(\frac{\partial{f}}{\partial{x_i}}\right)^2}=1 + \left|\nabla{f}\right|^2[/latex].
Evo, kolega Gino i ja (velikom većinom on  ) smo ipak uspjeli rješiti, pa ako nekoga zanima... ) smo ipak uspjeli rješiti, pa ako nekoga zanima... 
Dakle, želimo pokazati da je 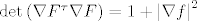 . .
Vrijedi 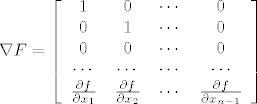 . zašto ne radi \vdots? . zašto ne radi \vdots?
Sada koristimo Binet - Cauchyjevu produktnu formulu, iz koje slijedi:
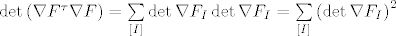 . Ovjde nam . Ovjde nam 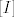 označava da sumiramo po rastućim označava da sumiramo po rastućim  -torkama iz skupa -torkama iz skupa  , dok nam , dok nam 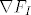 označava označava 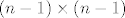 matricu dobivenu iz matrice matricu dobivenu iz matrice 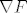 tako da joj je tako da joj je  -ti redak jednak -ti redak jednak 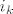 -tom retku matrice -tom retku matrice 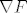 , , 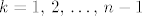 , , 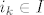 . (Odnosno, dobivena je tako da iz matrice . (Odnosno, dobivena je tako da iz matrice 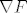 izbacimo onaj redak čiji se redni broj ne pojavljuje u izbacimo onaj redak čiji se redni broj ne pojavljuje u  -torci -torci 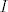 .) Jasno je da rastućih .) Jasno je da rastućih  -torki postoji točno -torki postoji točno  , naime, koji god broj da izbacimo iz skupa , naime, koji god broj da izbacimo iz skupa 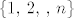 dobijemo jednu (točno jednu!) takvu dobijemo jednu (točno jednu!) takvu  -torku. -torku.
Izračunajmo najprije koliko je 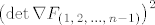 . .
Očito je 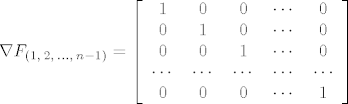 , stoga je , stoga je 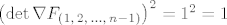 . .
Dalje, za svaku ostalu rastuću  -torku jasno je da ćemo "uzeti" -torku jasno je da ćemo "uzeti"  -ti redak, a nećemo "uzeti" jedan od prvih -ti redak, a nećemo "uzeti" jedan od prvih 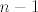 , neka je , neka je 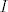 jedna takva rastuća jedna takva rastuća  -torka i neka je -torka i neka je 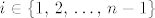 onaj kojeg nismo uzeli. Promotrimo sada onaj kojeg nismo uzeli. Promotrimo sada  -vi (kada je -vi (kada je  postupamo isto kao što ćemo sada objasniti, pa ne treba taj slučaj posebno razmatrati, isto u slučaju postupamo isto kao što ćemo sada objasniti, pa ne treba taj slučaj posebno razmatrati, isto u slučaju 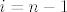 ) i ) i  -vi redak matrice -vi redak matrice 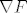 , oni su redom , oni su redom  -vi i -vi i  -ti redak matrice -ti redak matrice 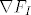 . .

U svakom retku (osim u zadnjem) matrice 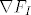 nalazi se jedna i samo jedna nalazi se jedna i samo jedna  , a ostalo su , a ostalo su  . Sada se sjetimo definicije determinante, jedini ne-nul sumand će biti onaj kada u svakom retku osim u zadnjem uzmemo tu jednu jedinicu, što će reći da iz zadnjeg retka moramo uzeti element koji se nalazi u . Sada se sjetimo definicije determinante, jedini ne-nul sumand će biti onaj kada u svakom retku osim u zadnjem uzmemo tu jednu jedinicu, što će reći da iz zadnjeg retka moramo uzeti element koji se nalazi u  -tom stupcu. Dakle, -tom stupcu. Dakle,
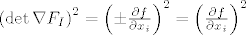 . .
Konačno,
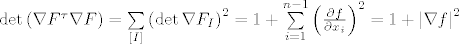 . .
|






