| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
SickJedi
Moderator

Pridružen/a: 01. 10. 2004. (16:41:56)
Postovi: (3BC)16
Spol: 
Lokacija: Esperantija
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
SickJedi
Moderator

Pridružen/a: 01. 10. 2004. (16:41:56)
Postovi: (3BC)16
Spol: 
Lokacija: Esperantija
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 10:27 pet, 30. 12. 2005 Naslov: Postano: 10:27 pet, 30. 12. 2005 Naslov: |
    |
|
|
Primjer na Z nije dobar. Pitanje neprekinutosti i diferencijabilnosti za takve funkcije nije standardno.
Postoji Weierstrassova funkcija:
Za [latex]a\in\langle0,1\rangle[/latex] i [latex]b\in\bf N[/latex] neparan Weierstrassovu funkciju definiramo s pomoću reda:
[latex]
f(x) := \sum_{k=0}^\infty a^k\cos(b^k\pi x)\;.
[/latex]
a) Dokazati da je [latex]f [/latex]neprekinuta na [latex]\bf R[/latex].
b) Napisati red za diferencijalni kvocijent [latex]{f(x+h)-f(x)\over h}[/latex] u obliku [latex]A_n+B_n[/latex], gdje [latex]A_n[/latex] predstavlja zbroj prvih [latex]n[/latex] članova reda,
a [latex]B_n[/latex] preostalih. Pokazati da vrijedi:
[latex]
\left|{f(x+h)-f(x)\over h}\right| \ge |B_n|-|A_n| \;,
[/latex]
gdje je [latex]|A_n|<{\pi a^n b^n\over ab-1},[/latex] a [latex]|B_n| > {2\over3}a^n b^n[/latex].
c) Pokazati da iz [latex]ab>1+3\pi/2[/latex] slijedi da [latex]f'[/latex] ne postoji; dakle,
[latex]f[/latex] je svuda neprekinuta, ali nigdje nema derivaciju.
- Nenad
Primjer na Z nije dobar. Pitanje neprekinutosti i diferencijabilnosti za takve funkcije nije standardno.
Postoji Weierstrassova funkcija:
Za 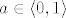 i i  neparan Weierstrassovu funkciju definiramo s pomoću reda: neparan Weierstrassovu funkciju definiramo s pomoću reda:
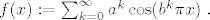
a) Dokazati da je 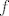 neprekinuta na neprekinuta na 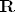 . .
b) Napisati red za diferencijalni kvocijent 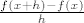 u obliku u obliku 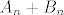 , gdje , gdje 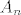 predstavlja zbroj prvih predstavlja zbroj prvih  članova reda, članova reda,
a 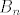 preostalih. Pokazati da vrijedi: preostalih. Pokazati da vrijedi:
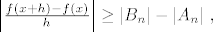
gdje je 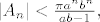 a a 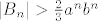 . .
c) Pokazati da iz 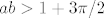 slijedi da slijedi da 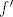 ne postoji; dakle, ne postoji; dakle,
 je svuda neprekinuta, ali nigdje nema derivaciju. je svuda neprekinuta, ali nigdje nema derivaciju.
- Nenad
|
|
| [Vrh] |
|
Drvena Škrinjarić
Forumaš s poteškoćama u pisanju


Pridružen/a: 20. 12. 2005. (22:24:19)
Postovi: (11)16
Lokacija: isto u trajnoj odsutnosti (dok me ne zbrišu)
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
Malik Titntilinić
Gost
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
SickJedi
Moderator

Pridružen/a: 01. 10. 2004. (16:41:56)
Postovi: (3BC)16
Spol: 
Lokacija: Esperantija
|
|
| [Vrh] |
|
Drvena Škrinjarić
Forumaš s poteškoćama u pisanju


Pridružen/a: 20. 12. 2005. (22:24:19)
Postovi: (11)16
Lokacija: isto u trajnoj odsutnosti (dok me ne zbrišu)
|
 Postano: 2:07 sub, 31. 12. 2005 Naslov: Postano: 2:07 sub, 31. 12. 2005 Naslov: |
    |
|
|
[quote="venovako"]Jel bi ti se dalo mozda raspisati pojmove "vrlo malo", "vecina" itd.
Zvuci zanimljivo, a nemam navedene knjige...[/quote]
(Nema to nikakve posebne veze s Brownovim gibanjem. I taj "hint" uopće nisam napisao ja.)
U topološkom prostoru (pa specijalno u metričkom prostoru) skup A je [i]rijedak[/i] ili [i]nigdje gust[/i] ako mu je nutrina zatvarača prazan skup, tj. [latex]\mathrm{Int}(\mathrm{Cl}(A))=\emptyset[/latex]
Skup S je [i]mršav[/i] ili [i]prve kategorije[/i] ako je prebrojiva unija rijetkih skupova, tj. postoji niz mršavih skupova [latex](A_n)[/latex] takav da je [latex]S=\cup_{n}A_n[/latex]
Mršavi skupovi predstavljaju "malene skupove u topološkom smislu".
Preciznije, poznati [i]Baireov teorem[/i] kaže:
[b]Potpuni metrički prostor X je skup [i]druge kategorije[/i], tj. X nije mršav skup, tj. potpuni metrički prostor se ne može prikazati kao prebrojiva unija rijetkih skupova.[/b]
To naprimjer znači da komplement mršavog skupa nije mršav skup nego je "puno veći u topološkom smislu". Prebrojivo mnogo mršavih skupova ne može iscrpsti cijeli prostor.
Gledajmo sad skup [latex]C([0,1])[/latex] svih neprekidnih funkcija [0,1]->R. (Radi određenosti i jednostavnosti.)
Na njemu definiramo metriku ("udaljenost" dviju funkcija):
[latex]d(f,g)=\max\{|f(x)-g(x)|:x\in[0,1]\}[/latex]
i uz nju [latex]C([0,1])[/latex] postaje potpuni metrički prostor.
Neka je S skup svih funkcija iz [latex]C([0,1])[/latex] koje su derivabilne u barem jednoj točki iz [0,1].
Tada je S mršav skup u [latex]C([0,1])[/latex]
| venovako (napisa): | Jel bi ti se dalo mozda raspisati pojmove "vrlo malo", "vecina" itd.
Zvuci zanimljivo, a nemam navedene knjige... |
(Nema to nikakve posebne veze s Brownovim gibanjem. I taj "hint" uopće nisam napisao ja.)
U topološkom prostoru (pa specijalno u metričkom prostoru) skup A je rijedak ili nigdje gust ako mu je nutrina zatvarača prazan skup, tj. 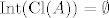
Skup S je mršav ili prve kategorije ako je prebrojiva unija rijetkih skupova, tj. postoji niz mršavih skupova 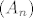 takav da je takav da je 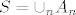
Mršavi skupovi predstavljaju "malene skupove u topološkom smislu".
Preciznije, poznati Baireov teorem kaže:
Potpuni metrički prostor X je skup druge kategorije, tj. X nije mršav skup, tj. potpuni metrički prostor se ne može prikazati kao prebrojiva unija rijetkih skupova.
To naprimjer znači da komplement mršavog skupa nije mršav skup nego je "puno veći u topološkom smislu". Prebrojivo mnogo mršavih skupova ne može iscrpsti cijeli prostor.
Gledajmo sad skup 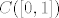 svih neprekidnih funkcija [0,1]→R. (Radi određenosti i jednostavnosti.) svih neprekidnih funkcija [0,1]→R. (Radi određenosti i jednostavnosti.)
Na njemu definiramo metriku ("udaljenost" dviju funkcija):
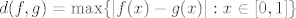
i uz nju 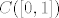 postaje potpuni metrički prostor. postaje potpuni metrički prostor.
Neka je S skup svih funkcija iz 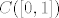 koje su derivabilne u barem jednoj točki iz [0,1]. koje su derivabilne u barem jednoj točki iz [0,1].
Tada je S mršav skup u 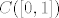
|
|
| [Vrh] |
|
šumeći
Gost
|
|
| [Vrh] |
|
Drvena Škrinjarić
Forumaš s poteškoćama u pisanju


Pridružen/a: 20. 12. 2005. (22:24:19)
Postovi: (11)16
Lokacija: isto u trajnoj odsutnosti (dok me ne zbrišu)
|
 Postano: 4:44 sub, 31. 12. 2005 Naslov: Postano: 4:44 sub, 31. 12. 2005 Naslov: |
    |
|
|
Istina, to je također dobar (čisto egzistencijalni) dokaz da postoje neprekidne funkcije koje nisu derivabilne niti u jednoj točki te da ih ima "puno više" nego neprekidnih funkcija koje su derivabilne u barem jednoj točki. Samo sad je ovo "puno više" u bitno drukčijem smislu.
Brownovo gibanje (standardizirano) je slučajni proces čije trajektorije su sve funkcije iz [latex]C([0,+\infty\rangle)[/latex], a gotovo svaka ("gotovo svaka" u smislu pripadne Brownove vjerojatnosne mjere) trajektorija mu nije derivabilna niti u jednoj točki. Drugim riječima, obzirom na tu Brownovu vjerojatnosnu mjeru, vjerojatnost da je trajektorija derivabilna u barem jednoj točki je jednaka 0. Dakle, takvih trajektorija ima "jako malo" ("zanemarivo malo") naspram onih preostalih (sasvim "kaotičnih" i koje je teško predočiti). Pa specijalno postoji barem jedna trajektorija koja nije derivabilna niti u jednoj točki.
Što se tiče ovog "malo" i "puno", čovjek bi eventualno mogao prigovoriti zašto bismo gledali baš Brownovo gibanje a ne neki drugi slučajni proces (recimo neki čije su sve trajektorije derivabilne), ali ima to svojih fizikalno-filozofskih opravdanja. "Teorija kaosa" ipak nije baš neki argument u "čistoj" matematici. :lol:
Ja sam primarno imao na umu "malo/puno" u topološkom smislu, dok je ovo drugo "malo/puno" u smislu teorije mjere. To su međusobno neovisni koncepti. Ali eto, u oba smisla izlazi da funkcija za koje pita SickJedi ima "puno" za razliku od "lijepih" kojih ima "malo". 8)
[size=7]Naši dragi brucoši se ne trebaju zabrinjavati oko toga kamo je ova rasprava otišla. Neće to biti na kolokviju...[/size]
Istina, to je također dobar (čisto egzistencijalni) dokaz da postoje neprekidne funkcije koje nisu derivabilne niti u jednoj točki te da ih ima "puno više" nego neprekidnih funkcija koje su derivabilne u barem jednoj točki. Samo sad je ovo "puno više" u bitno drukčijem smislu.
Brownovo gibanje (standardizirano) je slučajni proces čije trajektorije su sve funkcije iz 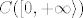 , a gotovo svaka ("gotovo svaka" u smislu pripadne Brownove vjerojatnosne mjere) trajektorija mu nije derivabilna niti u jednoj točki. Drugim riječima, obzirom na tu Brownovu vjerojatnosnu mjeru, vjerojatnost da je trajektorija derivabilna u barem jednoj točki je jednaka 0. Dakle, takvih trajektorija ima "jako malo" ("zanemarivo malo") naspram onih preostalih (sasvim "kaotičnih" i koje je teško predočiti). Pa specijalno postoji barem jedna trajektorija koja nije derivabilna niti u jednoj točki. , a gotovo svaka ("gotovo svaka" u smislu pripadne Brownove vjerojatnosne mjere) trajektorija mu nije derivabilna niti u jednoj točki. Drugim riječima, obzirom na tu Brownovu vjerojatnosnu mjeru, vjerojatnost da je trajektorija derivabilna u barem jednoj točki je jednaka 0. Dakle, takvih trajektorija ima "jako malo" ("zanemarivo malo") naspram onih preostalih (sasvim "kaotičnih" i koje je teško predočiti). Pa specijalno postoji barem jedna trajektorija koja nije derivabilna niti u jednoj točki.
Što se tiče ovog "malo" i "puno", čovjek bi eventualno mogao prigovoriti zašto bismo gledali baš Brownovo gibanje a ne neki drugi slučajni proces (recimo neki čije su sve trajektorije derivabilne), ali ima to svojih fizikalno-filozofskih opravdanja. "Teorija kaosa" ipak nije baš neki argument u "čistoj" matematici. 
Ja sam primarno imao na umu "malo/puno" u topološkom smislu, dok je ovo drugo "malo/puno" u smislu teorije mjere. To su međusobno neovisni koncepti. Ali eto, u oba smisla izlazi da funkcija za koje pita SickJedi ima "puno" za razliku od "lijepih" kojih ima "malo". 
Naši dragi brucoši se ne trebaju zabrinjavati oko toga kamo je ova rasprava otišla. Neće to biti na kolokviju...
|
|
| [Vrh] |
|
domaći_su_pravi_maj
stori
Gost
|
|
| [Vrh] |
|
guja-djevojka
Gost
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 12:49 sub, 31. 12. 2005 Naslov: Postano: 12:49 sub, 31. 12. 2005 Naslov: |
    |
|
|
@Drvena Škrinjarić:
Ma tko bi više znao, jesi li me hintao ti, neka tvoja alternativna osobnost, ili netko iz lavine alias-freakova koju ste pokrenuli :)
Bojim se da bi stvari koje su mi ostale za uvidjeti i/ili pitati te otišle predaleko u OT, pa ih možemo pretresti nekom drugom prilikom...
Svakako, hvala na intrigantnoj raspravi!
Zaslužena [tt]++karma[/tt] :)
@Drvena Škrinjarić:
Ma tko bi više znao, jesi li me hintao ti, neka tvoja alternativna osobnost, ili netko iz lavine alias-freakova koju ste pokrenuli 
Bojim se da bi stvari koje su mi ostale za uvidjeti i/ili pitati te otišle predaleko u OT, pa ih možemo pretresti nekom drugom prilikom...
Svakako, hvala na intrigantnoj raspravi!
Zaslužena ++karma 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
|








